From the “Simple English Wikipedia”1:
The Lorentz Factor is the name of the factor by which time, length, and “relativistic mass” change for an object while that object is moving and is often written γ (gamma). This number is determined by the object’s speed in the following way:
$\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$
Where v is the speed of the object and c is the speed of light (expressed in the same units as your speed). The quantity (v/c) is often labeled β (beta) and so the above equation can be rewritten:
$\gamma = \frac{1}{\sqrt{1 - \beta^2}}$
Lets examine the Lorentz equation to see what it is actually describing. In the Reciprocal System, the speed of light, c, is unity (1.0) in natural units of space and time—one unit of space per one unit of time. Conventional science uses “man-made” units that are derived by some kind of consensus. For example, the meter (meaning “measure”) was defined as one ten-millionth of the distance between the North Pole and the Equator. For the most part, conventional units are arbitrary. However, the Reciprocal System’s natural units are a consequence of the structure of nature, inherent in everything.
Starting with the velocity component, the factor v/c is simply normalization to unity, much like converting a range of values to percentages. Since the value of c is 1.0 in the Reciprocal System, the velocity in natural units is already normalized and this can just be reduced to v, making the concept of β unnecessary, as β represents the same consequence for arbitrary units.
We now have a normalized system of 1-v2. Knowing that unity is the speed of light, this part of the equation is actually saying: c-v2 (in natural units). Because c = 1, cn = 1 and n can have any value, so this part of the equation is actually . But when the square root function is considered, it becomes apparent that n = 2 and this Lorentz Factor is nothing more than the disguised equation of a right triangle that has been adjusted to express the speed of light a unit hypotenuse:
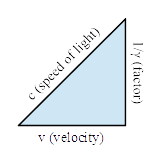 $\frac{1}{\gamma} = \sqrt{c^2-v^2}$
$\frac{1}{\gamma} = \sqrt{c^2-v^2}$
$\left( \frac{1}{\gamma} \right)^2 = c^2-v^2$
$c^2 = \left( \frac{1}{ \gamma} \right)^2 + v^2$
Alas, science also tends to overlook one of the more interesting properties of the square root—that the function returns two solutions, a positive one and a negative one. The negative one is ignored (though the absolute value is never included in the Lorentz equation), because it would indicate that time, length and relativistic mass could also be negative. But if you consider both solutions simultaneously, then a bigger problems arises… they cancel each other out and you end up with the classic “division by zero” problem that allows you to do things like proving 2=1.2 (So don’t mention it and hope nobody notices.)
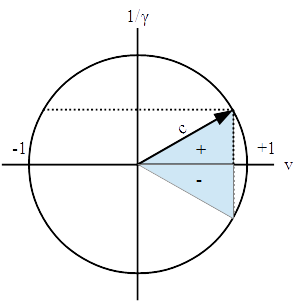
One should also note that the equation for a right triangle is also the equation for a circle: , where r is the radius. Because r = c = 1, this is a unit circle, with the velocity on the x axis and the Lorentz factor being the corresponding value on the y axis.
By plotting (v, 1/γ) in its entirety, the reciprocal relationship becomes clearer. What immediately stands out is that a velocity can drop all the way to -1, the speed of light running backwards. That may sound a bit strange, but once identified in conventional terms, it is a very familiar concept.
 In the Reciprocal System, the speed of light (unit speed) is the fulcrum between motion in space and motion in time. As such, it is the upper limit of both of those motions, essentially being the maximum speed of the universe, which is referred to as the progression of the natural reference system.
In the Reciprocal System, the speed of light (unit speed) is the fulcrum between motion in space and motion in time. As such, it is the upper limit of both of those motions, essentially being the maximum speed of the universe, which is referred to as the progression of the natural reference system.
You can only slow down from this speed. In space, you add time, so the speed of 1s/1t becomes 1s/nt. In time, you add space going from 1t/1s to 1t/ns, remembering that when you cross the unit speed boundary, inversion takes place and speed, s/t, becomes energy, t/s.
This is indicated in the Lorentz Factor, because any value where v>1 becomes undefined—there is no solution to the equation, because you would be moving at a velocity that is faster than the fastest velocity possible for the Universe. The system is only solvable if -1 ≤ v ≤ +1.
Anything (photons, particles, atoms, molecules, etc) being carried by this progression will be moving at this “maximum speed of the universe.” Photons, having no net displacement in space or time (in a vacuum) have no resistance to this speed and will therefore be carried at this maximum speed, which is why we call it the speed of light, or in the Reciprocal System, unit speed, and why the speed of light is constant in all reference frames in Relativity. Photons are not actually moving on their own; they are just being carried by the progression—no relative motion to the speed of the progression.
This is why the speed of light, the maximum speed of the Universe, cannot be exceeded by any velocity in space.3 It has nothing to do with “infinite mass” or an object shrinking into nonexistence, which is how the Lorentz Factor is interpreted.
The relations in the Lorentz Factor, understood as a unit circle, do occur in the Reciprocal System—but under different names. Larson unknowingly uses it as the basis of his initial motions.
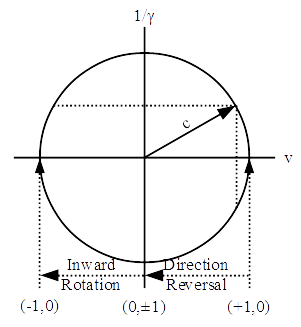 The problem is better understood in the complex plane, where the gamma function represents the imaginary axis (1/γ = -γ). By default, the Universe is expanding at unit speed, having the coordinates of (+1,0) on the diagram.
The problem is better understood in the complex plane, where the gamma function represents the imaginary axis (1/γ = -γ). By default, the Universe is expanding at unit speed, having the coordinates of (+1,0) on the diagram.
Larson then introduces the concept of a direction reversal, which results in a linear vibration. This is moving inward (left on the v axis) to the coordinates (0,±1). The progression velocity appears to stop (v=0), but there is now a split across the gamma axis, which is “imaginary” and rotational, creating the two, oppositely-directed rotations that are known as a birotation.4 The resolution of this birotation can be expressed by Euler’s formula using the exponential functions:
$\frac{e^{+i \gamma} + e^{-i \gamma}}{2} = cos(\gamma)$
So this “direction reversal” results in a cosine function, which Larson defines as a photon—the core of his rotating systems.5
Now that he has this ±γ “line” to rotate, Larson adds an inward scalar rotation to the photon, moving the net motion to the (-1,0) coordinate with a single speed solution, creating the rotational base, whose net motion opposes the progression at the same velocity, the speed of light running backwards that we call gravity, a very familiar concept.
Essentially, the Lorentz Factor is just a kludge hiding the use of imaginary quantities to describe a gravitational field structure, in a fashion similar to the imaginary quantities used to describe electric and magnetic fields. This gravitational opposition to the progression is what gives the appearance of increasing mass—even though mass remains constant—since a “heavier” object must have more gravitational pull and be harder to move.
The RS2 Approach
The Lorentz Fudge is a 1-dimensional solution to a 2-dimensional problem, as is Larson’s definition of the rotational base. However, the Universe is 3-dimensional and as William Hamilton discovered, it takes 4 dimensions to solve a 3-dimensional rotation: the quaternion.
The RS2 solution was to upgrade the complex plane of the corrected Lorentz Factor and replace it with a quaternion. This, however, changes Larson’s 2-unit approach of speed and energy into a 4-unit system of +1, i, i.j and i.j.k=-1. This resulted in a far more accurate representation of the photon, changing it from a linear vibration to a quaternion rotation with similar characteristics, but including electromagnetic properties with a 1-dimensional, electric rotation (k) combined with a 2-dimensional, magnetic rotation (i.j). Since i.j = k, a birotation can be formed along electromagnetic lines, using i.j.(-k), providing similar behavior to Prof. KVK Nehru’s original birotation model.
This will be elaborated on in a future paper, but just wanted to note the RS/RS2 difference.
Summary
-
The Lorentz Factor is the equation of a right triangle, where speed is normalized for a unit speed of light.
-
Ignoring the negative roots and velocities of the equation conceals the fact that the Lorentz Factor is actually just a unit circle.
-
Unit speed is the maximum speed the physical universe is capable of, expressed in the Reciprocal System as the outward progression of the natural reference system.6
-
The minimum speed is negative unity, the inward motion expressed by gravitation.
-
The default speed of the Universe is unity. When a conventional object “at rest” is accelerated, what is actually happening is that the inward motion of gravity is being neutralized. A rocket isn’t increasing its speed by thrust—the thrust is reducing the effect gravitation is having upon it, allowing it to return to the default speed of unity (the speed of light).
-
It is impossible to accelerate an object past the speed of light in space, because you are not adding velocity—you are reducing resistance and once that resistance is gone, you are done. This is the situation in particle accelerators and why electromagnetic systems cannot accelerate a particle past the speed of light. All they can do is reduce the resistance preventing the particle from moving at the speed of light.
-
The circular form of the Lorentz Factor produces similar results to Larson’s construction of the rotational base.
-
When the 1-dimensional interpretation is upgraded to three dimensions, the linear vibration of the photon becomes a quaternion rotation possessing electromagnetic characteristics, such as TE, TM and TEM modes.
What the Lorentz Factor comes down to is a device that is used to try to understand the inward, “backwards speed of light” motion of gravitation, similar to Ptolemy's epicycle description of the reversal of planetary motion. But when placed in the proper context, one can see past the illusions of mathematics and understand the underlying concepts.
2 Let a=b. Then a2 = ab; a2+a2 = a2+ab; 2a2 = a2+ab; 2a2-2ab = a2+ab-2ab; 2a2-2ab=a2-ab; 2(a2-ab)=1(a2-ab); cancel (a2-ab) from both sides gives 2=1.
3 I did qualify that, because faster-than-light motions are commonplace in the Reciprocal System, but manifest differently than “warp drive.” The translational velocities are always less then or equal to unit speed.
4 K.V.K. Nehru, “The Law of Conservation of Direction,” Reciprocity 18 № 3 page 3.
5 Larson’s solution is 2-dimensional; the 3-dimensional solution proposed by RS2 uses a quaternion rotation to accomplish the reversal, resulting in a more complex structure of the photon.
6 Known to astronomers as the Hubble Expansion.
