CHAPTER 23
Charges in Motion
When a negative* charge is added to an electron, the net total scalar speed of the charged particle is zero. But since the electron rotation has the inward scalar direction, while the charge has the outward direction, the two motions take place in different scalar dimensions. Thus the electron does not act physically as a particle of zero speed displacement, but as an uncharged electron and a charge. A moving charged electron therefore has both magnetic properties (those of moving uncharged electrons) and electrostatic properties (those of charges).
The conventional view is that electrostatic phenomena are due to charges at rest, and magnetic phenomena are due to charges in motion. But, in fact, charges in motion have exactly the same electrostatic properties as charges at rest. “It is one of the remarkable properties of electric charge that it is invariant at all speeds,”101 says E. R. Dobbs. So the motion of the charges is not, in itself, sufficient to account for electromagnetism. Some additional process must come into operation in order to enable a charged particle to exhibit magnetic properties when in motion. Whether this additional process involves the charge or the particle—the “carrier of the charge,” as it was called in a statement previously quoted—is not specifically indicated observationally. Present-day theory simply assumes that all effects are due to the charges. But since there are “carriers,” these are obviously the moving entities. The charges have no motion of their own; they are carried. Even on the basis of conventional theory, therefore, the electromagnetic phenomena are due to the motion of the carriers, not motion of the charges. The development of electromagnetic theory in Chapter 21 now verifies this conclusion, and identifies the carriers of the charges as “bare” electrons.
As noted in Chapter 13, a flow of charged electrons through a conductor (a time structure) follows the same course as the flow of uncharged electrons. But the charged electrons have a property that their uncharged counterparts do not have. They can also move freely through the gravitational fields of extension space, producing electromagnetic phenomena that correspond to the effects of the flow of current in conductors. This is illustrated by an arrangement such as that shown in Figure 25. In the center of the diagram is a wire through which a current is moving downward, as indicated by the arrow. (The conventional “direction of current flow” is opposite to the actual movement of the electrons, and is upward.) At the right is another conducting wire so arranged that a segment of the wire is hanging loose in a container filled with mercury. When a current is passed through this system in the same downward direction, the loose end of wire is attracted toward the center wire. At the left of the diagram is a vacuum tube through which a stream of electrons is also moving downward. This stream is attracted toward the center wire in the same way as the loose wire in the mercury container.
Figure 25
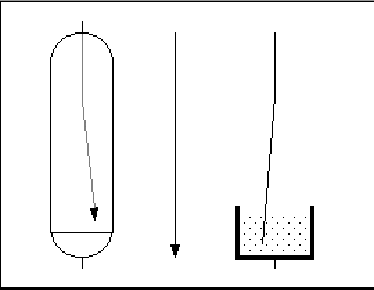
The movement of charged electrons through extension space is quite different in some other respects from the movement of uncharged electrons (space units) through matter. For instance, no electrical resistance is involved, and the motion therefore does not conform to Ohm’s law. But the magnetic effect depends only on the neutralization of one dimension of a quantity of gravitational motion by the translational motion of the electrons, and from this standpoint the collateral properties of the motion are irrelevant. As long as the motion of the charged electrons takes place in a gravitational field, the requirement for the production of magnetic effects is met.
On the basis of the general principles applying to electromagnetic forces, as defined in Chapter 21, the magnetic force on a charged particle in a magnetic field is the product of the magnetic field intensity B and a motion combination with the dimensions s2/t. The combination applicable to the motion of a charged particle, we find, is electric quantity q (measured as charge) multiplied by the particle velocity v. The force equation is then F = Bqv, with space-time dimensions
t/s2 = 2/s4 × s × s/t. The static force of the charge is F = qE, the dimensions of which are t/s2 = s × t/s3.
The electrostatic forces between the charges (units of Q) are independent of the magnetic forces due to the movement of the electrons (units of q). The total force acting on a charged electron in a magnetic field is then F = QE + Bqv. Since Q and q are numerically equal, because each electron takes one unit of charge, this force expression can be written F = q(E + Bv). The combined force is known as the Lorentz force. Lorrain and Corson comment on this force as follows:
The Lorentz force of equation 10-2 is intriguing. Why should v × B [velocity × magnetic field intensity] have the same effect as the electric field E? Clearly from equation 10-2, the particle cannot tell whether it “sees” an E or a v × B term… Thus v × B is somehow an electric field intensity.102
The authors then go on to say that the explanation is provided by the theory of relativity. But the space-time analysis shows that relativity has no bearing on this situation. From a physical standpoint, electric field intensity acts on a charged particle not as field intensity, but as a quantity of t/s3. Similarly, magnetic field intensity, t2/s4, acting against an electron moving with a velocity s/t has the effect of a quantity of (t2/s4 × s/t); that is, a quantity of t/s3. The magnitude of the physical result is the same in both cases.
This is not an unusual situation. On the contrary, it is common throughout all kinds of physical phenomena. The increase in temperature due to the addition of energy, for instance, depends entirely on the quantity of t/s that is added to the thermal motion. It is immaterial whether that energy increment is in the form of kinetic energy, chemical energy, electrical energy, or any other form of t/s.
The effect of v × B does differ from that of E in direction, and the expression given for the Lorentz force is therefore valid only in vectorial form. The electric force qE acts in the direction of the field, and because the field is radial, the charges to which the force is applied “are accelerated, gaining kinetic energy.”103 The effect of the magnetic forces follows a different pattern. For the reasons explained in Chapter 21, the force exerted by a magnetic field on a moving electron is perpendicular to the field. As noted in the discussion of electromagnetism, this perpendicular direction of the force is an unexplained anomaly in present-day physical thought. “The strangest aspect of the magnetic force on a moving charge is the direction of the force,”104 says a current textbook. When the origin of the magnetic field is understood, there is nothing strange about this direction. The scalar dimension of the motion of the electron is the dimension in which a portion of the gravitational motion is neutralized by the one-dimensional electron movement, and the residual two-dimensional motion necessarily exists in the two perpendicular dimensions.
The force aspect of this residual motion is also perpendicular to the magnetic field. If this is a magnetostatic field, it has the outward scalar direction, whereas the residual force has the inward scalar direction, and must therefore be in a different scalar dimension. If the field is electromagnetic, the forces are likewise in different dimensions, although the cause is different. As noted earlier, the motion of the uncharged electrons that constitute the electric current is in a scalar dimension other than that of the reference system. A freely moving charged particle, on the other hand, is moving in the space, and therefore in the scalar dimension, of the reference system. The acceleration of an electron moving in a uniform magnetic field is thus perpendicular both to the field and to the direction of motion. Such an acceleration does not change the magnitude of the velocity; it merely changes the direction. Motion at constant speed with a constant acceleration at right angles to the velocity vector is motion in a circle. If the particle is also moving in a direction perpendicular to the plane of the circle, the path of motion is spiral.
Most of the empirical knowledge that has been gained with respect to the nature and properties of sub-atomic particles and cosmic atoms has been derived from observations of their motion in electric and magnetic fields. Unfortunately, the amount of information that can be obtained in this manner is very limited. A particularly significant point is that the experiments that can be made on electrons by the application of electric and magnetic forces are of no assistance to the physicists in their efforts to confirm one of their most cherished assumptions: the assumption that the electron is one of the basic constituents of matter. On the contrary, as pointed out in Chapter 18, the experimental evidence from this source shows that the assumed nuclear structure of the atom of matter which incorporates the electron is physically impossible.
The theory postulating orbital motion of negatively* charged electrons around a hypothetical positively* charged nucleus, developed by Rutherford and his associates after their celebrated experiments with alpha particles, collided immediately with one of the properties of the charged electrons. A charged object radiates if it is accelerated. Since the charge itself is an accelerated motion (for geometrical reasons), the force required to produce a given acceleration of the charge is less than that required to produce the same acceleration of the rotational unit. But the charge is physically associated with the rotational combination, and must maintain the same speed. The excess energy is therefore radiated away. This loss of energy from the hypothetical orbiting electrons would cause them to spiral in toward the hypothetical nucleus, and would make a stable atomic structure impossible.
This obstacle in the way of the nuclear hypothesis was never overcome. In order to establish the hypothetical structure as physically possible, it would be necessary (1) to determine just why an accelerated particle radiates, and (2) to explain why this process does not operate under the conditions specified in the hypothesis. Neither of these requirements has ever been met. Bohr simply assumed that the motion of the electrons is quantized and can take only certain specific values, thus setting the stage for all of the subsequent flights of fancy discussed in Chapter 18. The question as to whether the quantum assumption could be reconciled with the reasons for the emission of radiation by accelerated charges was simply ignored, as was the even more serious problem of accounting for the assumed coexistence of positive* and negative* charges at separations much less than those at which such charges are known to destroy each other. It should be no surprise that Heisenberg eventually had to conclude that the nuclear atom he helped to develop is not a physical particle at all, but is merely a “symbol,” that is, a mathematical convenience.
All of the foregoing discussion of the phenomena involving charges in motion has been carried out in terms of charged electrons. The same considerations apply, inversely in some respects, to charged positrons. Like the charged electrons, these positively* charged particles are capable of moving through space, and since their motion is outward, differing from that of the charged electrons only in rotational speed, they produce the same general kind of magnetic effect as the charged electrons. In the cosmic sector, the cosmic electric current is a flow of uncharged positrons through cosmic matter, and charged positrons moving through the cosmic gravitational fields in time have magnetic properties.
The rotational vibration that constitutes a charge may also be applied to other particles or to atoms. The charge on a atom or multi-unit particle and the unit of rotation that it modifies constitute a semi-independent component of that entity. The combination of charge and rotational unit remains as a constituent of the atom or particle, but vibrates independently, in the same manner as the magnetic motion combinations discussed in Chapter 19. Inasmuch as this vibrating combination has the same composition as a charged electron or positron—a unit rotation modified by a unit rotational vibration—it has the same electric and magnetic properties.
The charges on atoms may be either positive* or negative*. As explained in Chapter 17, however, negative* ionization is confined to a relatively small number of elements because an atom must have a negative rotation in order to acquire a negative* (= positive) charge, and effective negative electric rotations are confined almost entirely to the elements of Division IV. On the other hand, any element can take a positive* charge. If the rotation in the electric dimension of the atom is negative, so that the positive* charge cannot be applied in this dimension, it can be applied to the rotation in one of the magnetic dimensions. The magnetic rotation is always positive in the material sector. It follows that while the mobile sub-atomic particles are predominantly negative*—that is, electrons—the freely moving (gaseous) ions are predominantly positive*.
The charged particles with which we have been concerned in the foregoing pages are electrically charged. Since there are also particles that are capable of taking magnetic charges, the question arises, Why do we not observe magnetically charged particles? The explanation can be found in the requirement that the net rotational displacement of a material atom or particle must be positive. The magnetic displacement, which is the larger component of the total, must therefore also be positive. This means that only negative magnetic charges can be applied to material particles.
The particles with magnetic rotational displacement are the neutron and the neutrino. The neutron has no electric displacement and only a single unit of magnetic displacement. Addition of an oppositely directed (negative) unit of charge therefore reduces the net displacement to zero, and terminates the existence of the particle. The neutrino has both electric and magnetic rotational components, and can therefore take a magnetic charge, but when it is in this charged condition it cannot move through space, for reasons that will be explained in Chapter 24, where the role of the charged neutrino in physical processes will be examined in detail.
This chapter concludes the discussion of magnetism as far as this subject will be covered in the present volume. Before turning to a different subject, it will be appropriate to make a few comments on the contents of the last five chapters and their relation to the physical situation in general.
Because the theory of the universe of motion, the detailed development of which is being described in these volumes, is new to the scientific community, and conflicts with many ideas and beliefs of long standing, the presentation in the several volumes of this series has a two-fold objective. It is designed not only to report the findings of the investigation based on the new theory, but also to provide the evidence that is required in order to confirm the validity of the findings. It therefore needs to be emphasized that the points brought out in the discussion of magnetism in these five chapters have made a very significant contribution to the mass of confirmatory evidence that is now available.
The particular importance of the magnetic evidence lies in the fact that the theory defines a specific dimensional relation between electricity and magnetism. It follows that whenever the theory identifies the nature of an electric phenomenon, this identification carries with it the assertion that there also exists a corresponding magnetic phenomenon, differing only in that it is two-dimensional, while the electric analog is one-dimensional.
Thus we find from the theory that there is a one-dimensional rotational vibration, identified as an electric charge, which has the space-time dimensions t/s and gives rise to a variety of electrostatic phenomena. According to the theory, it necessarily follows that there must be a two-dimensional rotational vibration, a magnetic charge, with the dimensions t2/s2, that gives rise to an analogous variety of magnetostatic phenomena. The observations verify the existence of a class of phenomena of this type, and an analysis of the dimensions of the magnetostatic quantities shows that they are, in fact, related to the corresponding electric quantities by the factor t/s, as required by the theory.
The dimensional interaction between electricity and magnetism is a particularly significant demonstration of the predictive power of the theory. We find from theory that gravitation is a three-dimensional scalar motion, and that an electric current is a one dimensional flow of units with the dimensions of space through the three-dimensional gravitating objects. From this it follows that the interaction should leave a two-dimensional scalar residue, oriented perpendicular to the current flow. Observations show that such a residue does exist, and that the process which leads to its existence can be identified with the phenomenon known as electromagnetism. It further follows from the same premises that the equivalent of a two-dimensional scalar motion through a three-dimensional gravitating object leaves a one-dimensional scalar motion as a residue. This interaction can be identified with the observed process known as electromagnetic induction, and the residue can be identified as an electric current.
The principal dimensional consequences that can be inferred from the theoretical identification of the electric current, electromagnetism, and gravitation with one, two, and three dimensions of scalar motion, respectively, are thus definitely correlated with observed electric and magnetic phenomena. But this is only the groundwork of a massive accumulation of evidence confirming the dimensional relations derived from theory.
Contemporary science places a great deal of emphasis on the predictive power of new theories. This is probably an overemphasis, as the ability of a theory to correlate existing information is as important as its ability to point the way to new information, and is becoming increasingly important as the “multitude of different parts and pieces” that now constitutes physical theory continues to expand. In any event, it should be recognized that deductions from the premises of a theory that identify hitherto unknown relations among known phenomena are predictions in the same sense as asserting the existence of a hitherto unknown phenomenon.
For example, the postulate that motion is the sole constituent of the physical universe carries with it the consequence that all physical quantities can be expressed in terms of space and time only. This is a prediction. The assertions as to the relation between electric and magnetic quantities discussed in the foregoing paragraphs are likewise predictions based on the same premises. The fact that the development of the consequences of the postulates of the theory of the universe of motion in the pages of this and the preceding volume has led to a complete and consistent system of space-time dimensions applicable to mechanical, electric, and magnetic quantities is a verification of these predictions.
The verification of this prediction is all the more significant because the possibility of arriving at any consistent system of dimensions, even with the use of four or five basic quantities, is denied by the majority of physicists.
In the past the subject of dimensions has been quite controversial. For years unsuccessful attempts were made to find “ultimate rational quantities” in terms of which to express all dimensional formulas. It is now universally agreed that there is no one “absolute” set of dimensional formulas.16
A similar prediction concerning the numerical values of these physical quantities is also implicit in the postulates. Since it is postulated that motion exists only in discrete units, it follows that the other physical quantities, all of which are either motions, combinations of motions, or relations between motions, likewise exist only in discrete units related to the units of the basic motion. This means that when the physical relations are correctly stated, they contain no numerical values other than those specifically identifying numbers of units, such as the atomic number, for example. The so-called “fundamental constants of physics” and the multitude of “disposable constants” that appear in relations such as the equations of state, will all be eliminated.
This fact that the values of the “fundamental constants” have no physical meaning in the context of the theory of the universe of motion contrasts sharply with the place of these constants in current scientific thought, where they are regarded as the critical magnitudes that determine the nature of the universe. Paul Davies expresses the prevailing view in this statement:
The gross structure of many of the familiar systems observed in nature is determined by a relatively small number of universal constants. Had these constants taken different numerical values from those observed, then these systems would differ correspondingly in their structure. What is specially interesting is that, in many cases, only a modest alteration of values would result in a drastic restructuring of the system concerned.105
As we have seen in the pages of this and the preceding volume, some of these constants, the speed of light, the electron charge, etc., are natural units—that is, their true magnitude is unity—and the others are combinations of those basic units. The values that they take in the conventional measurement systems are entirely due to the arbitrary magnitudes of the units in which the measurements are expressed. The only way in which the constants could take the “different numerical values” to which Davies refers is by a modification of the measurement system. Such a change would have no physical meaning. Thus the possibility that he suggests in the quoted statement, and explores at length in the pages of his book The Accidental Universe, is ruled out by the unitary character of the universe. No physical relation in that universe is “accidental.” The existence of each relation, and the relevant magnitudes, are necessary consequences of the basic factors that define the universe as a whole, and there is no latitude for individual modification, except to the extent that selection among possible outcomes of physical events may be determined by probability considerations.
The clarification of these numerical relations to put them in terms of natural units is a gigantic task, and it is still far from being complete, but enough progress has been made, particularly in the fundamental areas, to make it evident that there is no serious obstacle in the way of continued progress toward the ultimate goal.
The special contribution of magnetism to the verification of these significant consequences of the postulates that define the universe of motion has been that, because of its intermediate position between the one-dimensional and three-dimensional phenomena, it, in a sense, ties the whole fabric of scalar motion theory together. Recognition of this point, early in the theoretical development, led to deferring consideration of magnetism until after the relations in the other major physical areas were quite firmly established. As a result, the investigation of magnetic phenomena is not as far advanced, particularly in quantitative terms, as the theoretical development in most of the other areas that have been covered.
There is also another factor that has limited the extent of coverage, one that is related to the objective of the presentation. This work is not intended as a comprehensive treatise on physics. It is simply an account of the results thus far obtained by development of the consequences of the postulates that define the universe of motion. In this development we are proceeding from the general principles expressed in the postulates toward their detailed applications. Meanwhile, the scientific community has been, and is, proceeding in the opposite direction, making observations and experiments, and working inductively from these factual premises toward increasingly general principles and relations. Thus the results of these two activities are moving toward each other. When the development of the Reciprocal System of theory reaches the point, in any field, where it meets the results that have been obtained inductively from observation and measurement, and there is substantial agreement, it is not necessary to proceed farther. Nothing would be gained by duplicating information that is already available in the scientific literature.
Obviously, the validity of existing theory in any particular area is one of the principal factors that determine just how far the new development needs to be carried in that area. As it happens, however, the previous work in magnetism, and to some extent in electricity as well, has followed along lines that are very different from those that are defined for us by the concept of a universe of motion, and the results of that previous work are, to a large extent, expressed in language that is altogether foreign to the manner in which our findings must necessarily be stated. This makes it difficult to determine just where we reach the point beyond which we are in agreement with previously existing theory. Whether the clarification of the electric and magnetic relations in the special areas covered in the preceding pages will be sufficient, together with a translation of present-day theory into the appropriate language, to put electricity and magnetism on a sound theoretical footing, or whether some more radical reconstruction of theory will be required, is not definitely indicated as yet.
