Dimensions of Motion

In the Reciprocal System, everything is based on scalar motion,¹ which is simply a ratio of some magnitude of space to some magnitude of time. This ratio constitutes a dimension of motion, where there are three, possible states:

1. Unity, where the magnitudes of the aspects of space and time are equal. This is the “default” condition of a dimension of motion, which Larson refers to as the progression of the natural reference system. Since unit motion equates to the speed of light, the default motion of the universe is outward at unit speed—in other words, everything in the universe wants to fly apart from everything else at the speed of light, just for the heck of it. No energy required.

2. Speed, where the temporal magnitude is larger than the spatial magnitude, results in motion that is less than unity. Speed forms our conventional frame of reference where everything is moving at sub-light speeds. Larson uses the ratio of s/t to represent speed, which is the conventional way to represent velocity—to move some amount of space per some amount of time.²

3. Energy, where the spatial magnitude is larger than the temporal magnitude, results in a motion that is greater than unity. Larson uses the ratio of t/s to represent energy, which is the conventional concept of mechanical work—how much time does it take to move something a specific distance.

   Over-unity, faster-than-light speeds are not directly observable from our conventional reference system, but we can observe how energy changes space through the use of a device known as force fields. These lines of force (t/s²) are lines of energy (t/s) per unit distance (s).

When a dimension is at unity, nothing manifests, as it is equivalent to the “expansion of the cosmos.” In our conventional reference system, the first unit of motion is speed, creating a material structure such as a particle or atom. The first unit of motion can also be energy, which also creates an “inverse” particle or atom that Larson calls “cosmic matter,” conventionally called antimatter.³

This difference between speed (s/t) and energy (t/s) defines the two-sector approach of the Reciprocal System, the material sector (speed, s/t, referenced to clock time) and the cosmic sector (energy, t/s, referenced to clock space).

Number of Dimensions

Now that we have this tristate “dimension of motion,” how many of these dimensions can be linked together to form a single, compound structure? Professor KVK Nehru in his paper, “Some Thoughts on Spin,” addresses this question as a problem in geometric stability—if you have orthogonal dimensions, how may can co-exist together in a stable form? His answer is just probability of arrangement:

In a closed group of operators, like [1 i j k], the result of the combination of any number of the basal elements is also a member of the same group. The result of any such combination can be known only if all the possible binary combinations of the elements are first defined in terms of the basal elements i, j and k themselves (besides, of course, the identity operator, 1). Let there be n basal elements (excluding the unit operator 1) in a group. Then the number of unique binary combinations of these elements, in which no element occurs twice, is n(n-1)/2. We can readily see that a group becomes self-sufficient (finite) only if the number of binary combinations of the basal elements is equal to the number of those basal elements themselves, that is:

$$\frac{n(n-1)}{2} = n$$

The only definite solution for n is 3. (Zero and infinity are other solutions.) Therefore if we regard space (time) as a group of orthogonal rotations, its dimensionality has to be three in order to make it self-sufficient dimensionally. Otherwise the number of dimensions either has to shrink to zero, or proliferate to infinity.⁴

Nehru’s analysis indicates the point of dimensional stability is three dimensions and all of the building blocks of the Reciprocal System are based on three dimensions of motion⁵ (three, scalar dimensions), evenly distributed across the material and cosmic sectors. Each dimension has three states, with the states of speed and energy constituting some kind of structure. Larson refers to these “offsets” from the state of unity as units of motion, where each dimension of motion has two units of motion, s/t and t/s:

Though there are six units of motion (numbered 1-6 on the diagram), you will never see Larson refer to more than three.⁶ When the fourth unit of motion is reached, the net motion is no longer speed, but energy, making the structure cosmic in nature, so the 4^th unit of “material” motion (looking at the table, left-to-right) is analogous to the 3^rd unit of “cosmic” motion (looking at the table, right-to-left) and the motion is no longer directly observable with our conventional instrumentation.

Any aggregate will have its net motion in one of these three units of motion, which Larson refers to as speed ranges:

1-x: low speed, first unit. This is the realm of conventional science and what we observe as our spatial “reality.”

2-x: intermediate speed, second unit. These motions are observable, but have inverse properties, such as white dwarf stars and inverse thermal motion (super-hot appearing cold).

3-x: ultra-high speed, third unit. Also observable as an intermediate speed motion, but with more pronounced effects, such as the anti-gravity motion of pulsars. Due to the dimensional reduction at this speed range, ultra-high speed motion tends to be linear (jets).

Larson uses the #-x format to indicate which unit of motion the speed is in. For example, 2-x says that the motion is in the 2^nd unit of motion, at some value less than the maximum for the unit.

The Concept of the Clock

In a universe of motion, everything is motion—and that includes the clock. Granted, conventional thinking says the clock is just “time,” but with two sectors of motion there are also two aspects of the clock, clock time and clock space. Taken together, the relation of space to time (or time to space) is motion, so the clock is motion with aspects of space and time, just like any other motion in the Reciprocal System.

Where the confusion comes in is what the clock represents. If we examine how we use clock time, it is normally in relationship to either duration or speed. It took 5 hours to unload that truck or that car is going 45 miles per hour down the road. In both cases, time is related to space (moving boxes a distance for a specific duration of time, or a distance per a duration). The clock is therefore the standard device we use to measure change, or as Larson would put it, the datum of measurement.

The only datum in the Reciprocal System is that of unit speed, from which all motion is measured. It is from this unit motion datum that displacements are made to create structure. But the default, “at rest” condition of the universe is to move at unit speed, the speed of light. Larson refers to this motion as the progression of the natural reference system.

This unit speed is what we call the clock—our datum of measurement. A common misunderstanding is that the progression (the expansion of the universe) moves with the “tick of the clock” in both space and time. This is incorrect. The progression IS the “tick” that moves everything else, because the progression does not move relative to itself—it stays “fixed” like the end of a tape measure. Each discrete unit of the progression is a “tick” of the clock.

When we make use of clock functions, we normalize that aspect (clock time or clock space). That simply means that we take a ratio, like driving 300 miles in 5 hours, and reduce the denominator to unity. 300 miles in 5 hours is normalized to 60 miles per hour—a speed. If it took you 6 hours to write 3 book reports, then you are working at a rate of 2 hours per report. We then use these normalized rates to predict future events. If you had 10 book reports to write, at 2 hours per report, then you’re looking at 20 hours of work.

In many scientific applications, the normalized component (the denominator of a ratio of motion) is just ignored because it is unity. The ratio of s/t simply become s, a distance, rather than a speed. When examining conventional scientific processes, keep a watchful eye out for this omission.

Displacements

A displacement is a measurement of how much something changed from a known point. In the Reciprocal System, that “point” is unit speed, the speed of light. The notation for particles and atoms use displacements rather than the ratio of speed, because it is actually that displacement “delta” that defines the atomic properties.

Displacements are simply the difference in one aspect of motion from unity:

$\frac{1}{3} - \frac{1}{1} = 2$ temporal displacement

$\frac{3}{1} - \frac{1}{1} = (2)$ spatial displacement

A displacement can either be in space or in time. In the Reciprocal System, a spatial displacement is distinguished from a temporal one by placing the number in parenthesis, like an accountant would for a negative number. “2” would be a temporal displacement of 2 (speed of 1/3, as compared to 1/1) and “(2)” would be a spatial displacement (speed of 3/1).

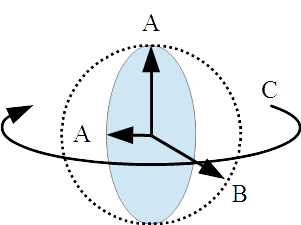Because we are dealing with a 3-dimensional universe of motion, Larson’s notation for displacements includes three components: a principle magnetic rotation, a subordinate magnetic rotation and an electric rotation. Notion for particles and atoms use three displacements, to represent displacements in the three, scalar dimensions in the A-B-C format. For example, oxygen is 2-2-(2), which means that the two, temporal rotations have a displacement in time of 2 units, coupled with a spatial rotation in the 3^rd scalar dimension of 2 units.

Displacements can also represent either material sector (3D space) or cosmic sector (3D time) structures, which Larson notates with an “M” or “C” prefix, as well as exchanging numbers in parenthesis by those, without. For example:

• M 2-2-(1) is material fluorine, atomic number 7.

• C (2)-(2)-1 is cosmic fluorine, also atomic number 7.

This seems to be unnecessary as the parenthesis on the two magnetic rotations clearly indicate to which sector the 3-dimensional structure belongs. Larson later uses the M/C designation with a superscript “*” to indicate a charged condition that cannot be represented in the displacement notation, so the notation does get used.

One final note on atomic displacements. For a particle, the A-B-C notation represents motion in three, scalar dimensions, minus the displacement of the rotational base.⁷ Larson refers to this as a “double rotating system” that Prof. KVK Nehru later identified as a solid rotation (the rotation of a ball, rather than a disk). Particles have single, double-rotating system whereas atoms have two, double-rotating systems. The displacements listed for an atom are the same for each of these double-rotating systems within the atomic structure.

---