Dialogue II

Below are reproduced further comments on D. B. Larson’s Nothing But Motion (NBM) and on Quasars & Pulsars (QP), interspersed with responses by the author. The correspondence from which this dialog is excerpted took place circa 1980.

1. KVK: Ref. p. 46, para 2, QP: If the n mass-units of a material aggregate are dispersed in time, no observer can encounter all of them at the same time. For example, all of the atoms in an object may not manifest at the same time because of the differences in their coordinate time, even if they are at the same stage of the progression.

DBL: Two atoms are in contact when they are within the equilibrium distance in either space or time, regardless of how far apart they may be in the other. They have to be at the same stage of the progression to make contact in space, but this has nothing to do with time. It is a result of the fact that even though two objects may be at the same point in the reference system, they are not at the same location in space unless they are also at the same stage of the progression.

2. KVK: Ref. p. 48, para 2, QP: This example of the two cardboard disks gives rise to two possibilities, which are polar opposites as far as the mutual direction of the coupled rotations are concerned. For a given direction of rotation of disk A, disk B could be posited either as rotating in the clockwise sense or in the counterclockwise sense. Do these dual possibilities in the model refer to any analogously distinguishable categories of the double rotating system of the atoms?

DBL: I have not considered this issue previously, and I do not want to express any firm conclusions without more extended consideration, but from my findings in the fields of electricity and magnetism, I would tentatively conclude that reversal of the direction of rotation would reverse the scalar direction. The resulting motion would be incompatible with the atomic structure.

3. KVK: Ref. p. 98, line 7, QP: Should not the word ‘active’ be replaced by the word ‘inactive’?

DBL: No. Beyond the unit level (the speed of light) motion takes place in two scalar dimensions.

4. KVK: Ref. p. 98, lines 13-16, QP: Firstly, it is not clear how ‘only one dimension of the explosion speed is coincident with the normal recession.’ For instance, the recession itself is not limited only to our line-of-sight. Secondly, it is not clear how the excess redshift and the recession redshift are to be connected, or why the former is proportional to the square root of the latter.

DBL: These items are also connected with the concept of scalar dimensions. I am enclosing copies of two pages of the introduction to Volume II of the new edition of the “Structure”, which should help to explain what I mean here. Motion at speeds beyond the unit level involves both a space magnitude and a time magnitude. It is therefore a two-dimensional scalar motion, only one dimension of which can be parallel to the dimension of the reference system.

5. KVK: p. 154, line 18, NBM: Should it not read: “…the ratio of the total magnitude of motion to the transmitted effect” rather than the converse?

DBL: Yes.

6. KVK: p. 154, lines 8-7 from bottom, NBM: The possible vibrational positions for the two-dimensional basic rotation do not seem to me to be nine, in view of the fact that the respective orientations of the initial vibrating units of both rotating systems are not independent of each other, after the formation of the double rotating system. It can be seen that the number of possible orientations for the vibrational displacement of one of the rotating systems of the atom is three. However, referring back to the two-disk analogy (p. 48, QP), the number of possible orientations for the initial vibration of the second rotating system is only two, because one of the three dimensions is already occupied by the first and there is no superimposition. As such, the total number of vibrational possibilities is six, of which one is occupied. Thus the inter-regional ratio must be 128(1 + 1/6) =149.33.

DBL: I cannot agree with your conclusions here: There are nine different combinations irrespective of geometrical considerations.

7. KVK: p. 163, NBM: In the calculation of the unit of electric mass, why is the 1/9 vibrational factor relevant, since what we are concerned with is the electric rotation.

DBL: The 1/9 factor applies to the distribution in space. The same factor applies to both the distribution of the electric rotation and the distribution of the possible positions of the vibrational units, but this does not mean that there is any connection between the two.

8. KVK: p. 6, para 3, Advance Printing of the first 11 chapters of Volume II¹: What is orientation? What is meant by the rotational force acting only during a portion of unit progression?

DBL: I use the word “orientation” in the sense defined in the dictionary; that is, position with respect to the environment. I suggest that you review the discussion of orientation in the references listed under that heading in the index of NBM, page 291.

9. KVK: The basic scalar reversals that make possible speeds other than unity are fundamental in the Theory. As such, a thorough understanding of their nature is important.

The givenness of the 1/1 unidirectional scalar progression is understandable. However, how the reversal of the scalar direction of the progression is accomplished in nature is not explained. In the existing pattern of thinking one posits a cause for a systematic variation of a state of affairs. Inasmuch as these reversals are systematic and not random (in order to produce a speed other than unity) it is not clear what sustains them. Why should the reversals occur at all since the ‘peace’ of the unidirectional progression has a greater probability? They stand merely as a logical necessity for the subsequent development of the theory.

DBL: Aristotle and his contemporaries insisted that continuity of position is the only condition that can be maintained without the application of some external influence. One of the essential steps toward a theory of motion was a recognition of the fact that a continuous uniform change of position is just as fundamental, and just as permanent, as a continuity of position. The essential feature is the continuity. What is needed now is recognition of the fact that the same considerations apply to direction. A continuous uniform change of direction is just as fundamental, and just as probable a condition, as a continuous direction. A motion with a continuous uniform change of direction is, of course, a simple harmonic motion. There is no more need for anything to sustain a simple harmonic motion than a unidirectional motion.

10. KVK: What is the nature of the connection between the scalar reversals and the vectorial directional reversals associated with them? In the case of a vibration that is a photon, since the vectorial reversal occurs at the end of each unit, it is not always in phase with the scalar reversal. Obviously the two (the scalar and the associated vectorial) directional reversals are connected: but as this connection is not explained, one wonders how the vectorial reversal ‘knows’ when to be in phase with the scalar reversal and when not to be, in order to produce a regular oscillation pattern.

DBL: The further changes in the pattern of reversals that, as you say, produce speeds other than unity, are mathematical possibilities. Each corresponds to a particular displacement magnitude (a particular number of units of energy in the phenomena of ordinary life). This displacement (or energy) content is what maintains the constant reversal pattern. The pattern cannot change unless energy is added or withdrawn.

11. KVK: The way the reversals are explained to be occurring, they can give rise to odd frequencies in a straightforward manner. However, the even frequencies are pictured to be accomplished by the systematic compounding of odd frequencies. Thus, for example, frequency 4 is obtained by the averaging of the multiple units of 5 and 3 that occur alternately. But if it is so possible to accomplish frequency 4 by way of compounding of 5 and 3, [(5+3)/2 = 4], why is it not possible to obtain non-integral frequencies, such as 4.33 for example, by the compounding of multiple units thus: (5+5+3)/3 = 4.33 etc.? Do we have to take recourse to an ad hoc constraint to avoid this?

DBL: In view of the systematic relation between number and probability (see item No. 13 below), the only place where two numbers are equally probable is the midpoint between successive numbers. In this situation (and no other), probability usually dictates an equal distribution between the two. In a situation such as that we are now considering, this distribution must be exactly equal in order to produce a regular pattern.

12. KVK: In the notation a b c of the atomic rotations, ‘a’ stands for the principal magnetic rotation and ‘b’ for the sub-ordinate magnetic rotation. The principal magnetic rotation is said to be effective in two dimensions while the subordinate magnetic rotation in one dimension (p. 128, NBM). How is this so? As both of them are two-dimensional rotations, each must be effective in two dimensions.

DBL: Two independent rotations of a disk (a one-dimensional rotation of a line) would produce two spheres, but a rotation of two inter-penetrated disks produces a spheroid, either an oblate spheroid with a volume proportional to a²b, or a prolate spheroid with a volume proportional to ab².

13. KVK: Ref. p. 48, para 3, QP: “…as a general principle low numbers are more probable than higher numbers…” Why should this be so? To be sure, this ‘general principle’ is not incorporated in the Fundamental Postulates.

DBL: You can demonstrate this with the standard coin tossing experiment. You will get two successive heads very often, three much less frequently, four still less often and so on. The same principle applies throughout the universe.

14. KVK: The electric charge is a one-dimensional rotational vibration, and is normally a modification of the existing one-dimensional rotation in the electric dimension. But the exception is the proton which is M 1 1 (1). In this case, if the electric charge is to be a modification of the rotation in the electric dimension it would be a negative charge, as in the case of an electron M 0 0 (1), since the rotation in the electric dimension is negative. As such, it is taken that this electric charge is a modification of the two-dimensional positive rotation (in the magnetic dimension). Consequently it will be a positive electric charge as we want.

But why does this positive electric charge, which is one-dimensional, take precedence over a magnetic charge, which should more naturally be the appendage to the basic two-dimensional rotation in M 1 1 (1)? Compare with the case of the neutrino M ½ ½ (1) which easily acquires a magnetic charge (on its 1 unit two-dimensional rotation) rather than an electric charge.

DBL: A charge opposes the rotation to which it is applied under ordinary circumstances, and in the particles (single rotating systems) the units are equal in size. Thus a negative charge added to the proton, M 1 1 (l), would increase its net total displacement to 2. As noted in NBM, it appears that two-unit single rotations are unstable, and tend to decay back to simpler components, unless they are able to acquire the second rotating system that is required for converting to mass 1 hydrogen. A second point in this connection is that a magnetic charge is not acquired easily. On the contrary, the evidence indicates (although the reason is still unknown) that acquisition of such a charge by a neutrino is a very rare event. Concentrations of charged neutrinos are produced only by an enormous number of interactions with matter over vast periods of time.

15. KVK: While a neutrino M ½ ½ (1) can easily acquire a magnetic charge, why does it not happen to a massless neutron M ½ ½ 0? (Of course, if it thus gets magnetically charged, its potential mass becomes actual.)

DBL: A positive magnetic charge added to either the neutrino or the massless neutron cancels the positive rotational displacement. The effective displacement of the charged neutrino is equal to that of the uncharged electron, and it acts like the electron. The effective displacement of a charged massless neutron would be that of the rotational base, zero, and there would be no effects that could be observed.

16. KVK: Why is the proton M 1 1 (1), having net rotational displacement in three dimensions and a mass of one atomic weight unit, not observed in the uncharged state, when theory does not preclude this?

DBL: The answer to this question is still in doubt.² It may be that there are too many neutrinos in the environment. As indicated in NBM, page 215, an uncharged proton and a neutrino can combine to form the mass one hydrogen isotope. It is possible that the uncharged proton never gets a chance to stay around long enough to be observed.

17. KVK: p. 52, lines 14-15, QP: “The atomic number of any… element is equal to its equivalent electric time displacement less two units.” Take for instance the case of He: 2 1 0. After accounting for one two-dimensional unit counteracting the opposite displacement of the basic photon we are left with a net displacement of 1 1 0. This must naturally yield an electric equivalent of (2×1²) + (2×1²) = 4 displacement units. What is the reason for specifying that one of these two (2×1²) units is not to be counted?

DBL: As you say, the helium atom has net displacements 1 1 0. If we eliminate one magnetic unit, we have the combination 1 0 0 (or 1 1 0 in the regular atomic notation). This is not an atom because it does not have enough effective displacement to form a double system. It is a base for the atomic rotation in the same way that the rotational base, M 0 0 0, is for rotation in general. We might call it an atom of zero atomic number. Thus there is only one 2×1² group of elements.

18. KVK: Is not the inward translational effect of the scalar rotation (gravity) proportional to the number of rotational displacement units? If yes, since the maximum number of unidirectional three-dimensional displacement units is 8, how to justify the number of units of the inward motion when it exceeds 8, as is the case of elements with atomic number greater than 8?

DBL: Gravitation is not a unidirectional motion. It is a rotationally distributed scalar motion. See the memorandum on scalar motion that I sent to you.

19. KVK. Ref. p. 98, para 2, QP: The ‘units of motion’ referred to here are displacement units, aren’t they? Why do these 7 units get distributed only between two dimensions? Why not between the three dimensions? Since the direction in time taken by the ultrahigh speed unit has no relation to the direction in space, probability principles require equal distribution among the three dimensions of space.

DBL: Motion in the region above unit speed takes place in two scalar dimensions because of the second unit status of this region. All that this means is that it takes two numerical magnitudes to define the motion, rather than the one that is sufficient for any motion below unit speed. It has nothing to do with the dimensions of the spatial reference system.

20. KVK: Then again, the connection between the recession redshift and the quasar redshift is not clearly explained. The recession redshift depends on the particular moment at which the explosion happens to take place. As such it should not bear a strict logical relation to the explosion redshift, since the time of occurrence of the explosion is determined by various local conditions and not strictly by its distance from us.

DBL: The difficulty that you mention with respect to the relation between the redshifts is merely a matter of the time required to transmit information. If an explosion occurs at a distance x from our location, the corresponding distance in the explosion dimension is 3.5x^½. This is the actual separation between us and the quasar in this dimension. But we see the explosion at spatial distance x, and we cannot get the quasar distance information instantaneously; that is, the quasar cannot appear to jump directly from x to 3.5x^½ What happens is that this information comes to us as fast as it can. The quasar appears to move at the speed of light in the explosion dimension until it reaches the 3.5x^½ distance, after which it recedes normally. The time required to make this adjustment is very short, and it is probable that we have never observed a quasar in the adjustment period.

21. KVK: Ref. p. 108-9, QP: Does the same gravitation oppose normal recession as well as the explosion? Or is it the portion left after countering the recession that is available to oppose the explosion? On p. 109, lines 1-2, what is meant by the dimension of recession and the dimension of quasar motion? Does it mean that since 1 unit recession is already present in one dimension of the three dimensions, the explosion motion takes the remaining two?

DBL: Yes, gravitation opposes each motion independently. In application to scalar motion, I am using the term “dimension” in the mathematical sense. An n-dimensional scalar motion is one that requires n separate numbers to define it. The example given in my dictionary is this: “a²b²c is a term of five dimensions”. Only one of these scalar dimensions of motion can be represented in the conventional spatial reference system. Any number of motions of an object that can be represented in the system can be combined vectorially into a one-dimensional resultant, and the magnitude of the resultant can be expressed by one number. What the reference system does is to subdivide the one dimension of motion into components by relating it to three dimensions of space. The two dimensions of motion above unit speed are scalar dimensions, and they are not vector quantities.

22. KVK: Ref, p. 123, lines 10-11, QP: But when the speed is changing should not one take the integral of v dt as the distance and not simply vt?

DBL: I see no advantage in so doing. What we are interested in is the average speed.

23. KVK: p. 60, para 3, QP: This phenomenon of positive ionization resulting from high temperature must be observable experimentally. It would then constitute an element of validation of the theory.

DBL: This is the ionization that the physicists and the astronomers talk about. They attribute it to the loss of successive electrons from the atomic structure as the temperature increases. My finding is that units of vibrational motion are added. This is, of course, a deduction from basic principles, but it is worth noting that it produces a more logical result. An increase in the energy content of the environment ought to result in processes that gain energy from the environment, rather than processes that lose energy to the environment.

24. KVK: Ref. p. 66, para 2, QP: Here is another venue for observational verification. During the past millions of years of the age of our planet, the local level of magnetic ionization must have increased. Can we devise experiments to measure this and then to correlate this change with (i) the change of isotopic proportions in the earth’s crust and (ii) the shift of the radioactive stability limit of the heavy elements that took place during this period? Also we may verify this correlation by comparing with systems of matter under a different ambient magnetic ionization level, as on distant planets.

DBL: The question as to when the magnetic ionization level on earth stepped up to the present level, which is almost certainly one unit, is not definitely indicated by the information now available. There are reasons to believe, however, that this change antedated the formation of the Solar System.

25. KVK: The half-lives of electron and proton are estimated to be about 2×10²¹ years and 10²⁷ years respectively. Could the chance encounters with the c-atoms (moving inward in time) be the cause for these spontaneous decays of electrons and protons?

DBL: I doubt if these estimates have any real meaning.

26. KVK: The process of the transition of a quasar from our time-space region to the space-time region of the cosmic sector looks to me analogous to the process of the transition of the solid state (of matter) from the time region to the gaseous state of the time-space region.

It is stated that the overcoming of cohesion in one dimension results in the liquid state and the vanishing of cohesion in three dimensions results in the gaseous state. While this is true, there is also an intermediate case of the vanishing of cohesion in two dimensions. My suggestion is that this constitutes the vapor state. The liquid state ends with the overcoming of cohesion in two dimensions.

Let us take a look at the analogy I was mentioning. Please refer to the Figure 4, p. 68, QP. For the ‘scalar inversion’ (by which I mean the transition from the time-space region to the space-time region) to happen, what is necessary is not unit speed in all the three dimensions (Figure 4c), but only unit speed in each of the two inactive dimensions. Since the conversion of unit speed to zero speed in time in the inactive dimensions (Figure 4d), is a normal, down-hill process in the cosmic sector, this addition of unit speed in the two inactive dimensions is sufficient to bring the situation of Figure 4a eventually to that of Figure 4d, and execute the complete scalar inversion. (Of course, the sub-luminal speed represented by T in Figure 4d, in the active dimension results in a distortion in the stationary three-dimensional temporal reference frame of the cosmic sector, showing up as motion in ‘equivalent time’).

Now the point I want to make is that, in exactly the same way, in our analogy, what ends the liquid state is the emancipation from cohesion in two dimensions only, and not in three. Availability of additional thermal energy, however, converts the vapor to gas by overcoming cohesion in the third dimension too.

Further—please see bottom para, p. 75, QP: here I am inclined to consider the structure of a cluster or galaxy of stars to be more analogous to that of a solid at high temperature, rather than a liquid as you suggest. The suggestion is perhaps based on the apparent fluid nature of the structure. But, insofar as the stars occupy equilibrium positions (under inward gravity and outward progression) they are analogous to the solid molecules which too occupy equilibrium positions (under outward gravity and inward progression), the apparent fluidity in the galactic instance is due to the different nature of the equilibrium.

Now my sketch below indicates the step by step analogy between the two processes I was mentioning—one involving transition from the time region to the time-space region, and the other from the time-space region to the space-time region. The numbers in the blocks indicate the number of dimensions of motion pertaining to that particular region in which it is shown. The ‘material rays' shown in the c-sector are the analogs of the cosmic rays of our sector.

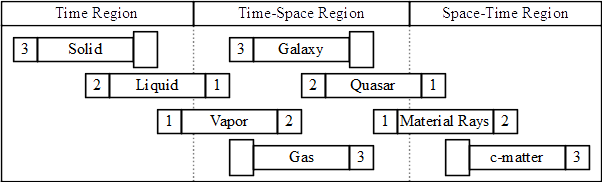
DBL: The idea of the vapor state having cohesion in only one dimension is an attractive one, and I gave it considerable attention 30 or 40 years ago when I was working on liquid and gas properties, I ran into quite a few problems in developing the idea, mainly because of the coexistence of the liquid and vapor states over such a wide range of temperatures, and I never reached any firm conclusions. I discontinued work in this area about 1960 when I decided to reduce my research activities and spend more time on writing about what I had already found out.

Your ideas as to the transition from the material to the cosmic sector are on the right track, although the situation as I find it is more complicated. You may be interested in comparing your diagram with the following one, taken from the manuscript of what will probably be my next book:

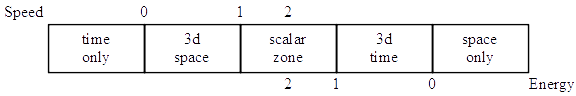
KVK: Why can’t there be electrical charged neutrons and massless neutrons, M+ ½ ½ (1) , M- ½ ½ (1) and M+ ½ ½ 0?

DBL: I presume it is because the charge, being a rotational vibration—half of full rotation—must modify a full rotational unit, but it cannot extend over two dimensions, as a two-dimensional unit can, and in the cases that you mention there is no full unit for it to modify.

27. KVK: It is still not clear what the origin of the secondary mass is: what is meant by ‘the initial level’ and ‘its motion in the time region’ (NBM, p. 161)?

DBL: The primary mass is a measure of motion that is defined as a relation of units of space to units of time. But since the equilibrium positions of the atoms of ordinary matter are inside unit space, some additional effects of their motions take place within the space units, and a portion of these internal effects is transmitted to the external region. These are relations of units of equivalent space to units of time. It seemed to me that the easiest way to grasp what is happening here would be to regard it as analogous to firing a gun from a moving vehicle. In order to arrive at the speed of the projectile, we have to take into account the initial level of speed, the speed of the vehicle, as well as the speed imparted by the explosive charge.

28. KVK: In view of the discrete unit postulate, the gravitational speed cannot be greater than 2 inward units. Now suppose there is an atom with Z = 50: does its atomic weight 100 give rise to 100 units of inward speed, that is, gravity? If not, how does the magnitude of the inward translational effect (gravity) of an element with Z = 50 differ from that of an atom with, say, Z = 30? How to account for this gravitational speed greater than 2 net units?

DBL: The total gravitational speed of each mass unit is always two units (one net inward unit). The effect of aggregation of the mass units is to increase the distribution of this total speed toward the location of the aggregate.

29. KVK: The entire heart of the quasar theory was explained in just one paragraph (QP, p. 98, top para). The total separation between zero speed in space and zero speed in (3-dimensional) time is taken to be 8 units. But in your diagram A (Reciprocity, VIII (4), p. 25) you show only a total of 6 units.

DBL: For this purpose you need to distinguish between the dimensions of space (or time) and the dimensions of motion (what I have called scalar dimensions). As I pointed out in the manuscript of The Neglected Facts of Science (Chapter 2), only one dimension of motion can be represented in the conventional spatial reference system. The magnitude of this one dimension of motion is resolved into three sub-magnitudes by the introduction of directions in space. Thus a one-dimensional scalar motion is three-dimensional in space.

From zero speed to zero energy in one scalar dimension is two equivalent units of speed (or energy). The total number of units from the absolute zero of speed to the absolute zero energy (three scalar dimensions) as thus six units. But each two-unit component of this total (each dimension) is subject to resolution into three dimensions of space. This means that there are eight equivalent one-dimensional spatial units when the one scalar dimension of motion is distributed three-dimensionally. Only one of these can be represented in the spatial reference system, but the magnitudes of the motion in time (equivalent space) can be defeated by the Doppler shifts. However, all relations in which the spatial equivalent of time is substituted for actual space are two-dimensional (see NBM, page 155). Consequently, the seven remaining equivalent space units are divided (usually equally) between the dimension that is coincident with the dimension of the reference system and the dimension in which the Doppler shift is unobservable.

30. KVK: Moreover, is this 8-unit separation in terms of speed units or in terms of speed displacement units? (since, if the displacement is n, the speed is 1/n+1 or n+1/1).

DBL: In these instances we are dealing with speed units. Displacement applies only to those phenomena, in which the effective quantities are the increments above unity.

31. KVK: See: “…the seven units are therefore divided equally between the two spatial dimensions that are now active.“ (p. 98, top para, QP). What is meant by ‘active’ here? Are you referring to the two spatial directions (p. 97, second para, QP ) in which there can‘t be a translational movement since translation is already taking place in one direction of the 3-dimensional space due to the recession. To be specific, let us imagine the x y z Cartesian system to locate the quasar. If translation due to the recession happens to be in the z-direction, the object cannot have a spatial speed in the x and y directions. If this is so, your words quoted above seem to mean to me that the 7-unit equivalent of the 1-unit quasar motion in time is divided between the x and y directions of space. Is this what you wanted to convey? But in the next sentence you say “The component of the explosion speed in the recession dimension is thus 3.50”. Here your words seem to mean that this 3.5 units show up in the z-direction of space, in which the recession speed is manifesting in the coordinate system.

Further, a few lines below you mention, “…only one dimension of the explosion speed is coincident with the normal recession…” Does not the explosion speed belong to a second scalar dimension, altogether different from the dimension in which the recession is taking place? How does one dimension of the explosion speed coincide with the recession? If the explosion speed is a two-dimensional scalar motion, why can’t both these scalar dimensions be other than the dimension of recession, in which case no dimension of the explosion speed coincides with the normal recession. That is, suppose a, b, c are the magnitudes of the scalar motions in the three scalar dimensions and let a represent the recession. If, then b and c pertain to the explosion motion, none of the dimensions of the explosion motion coincides with the recession dimension. How then the square-root of z_r arises is not clear.

DBL: The recession takes place in all three scalar dimensions. It follows that one of these three dimensions is coincident with one of the two dimensions of motion in equivalent space. The total magnitude of the motion in this effective dimension is the sum of the recession, z and the effective portion of the motion in equivalent space, 3.5z^½.

You should not try to visualize these motions in terms of the spatial reference system (the x y z Cartesian system to which you refer), because neither the low speed motion in the second and third scalar dimensions, nor any of the high speed (above unity) motions can be represented in that system. In dealing with these motions we have to deal entirely with magnitudes. When we talk about dimensions in connection with them, it is only in the mathematical sense, in which an n-dimensional quantity is one that requires n scalar magnitudes to define it. These dimensions are not the dimensions of the spatial reference system. Since the quantities with which we are dealing are the same in all cases—that is, units of motion—any one magnitude outside the reference system can be added to the magnitude represented in that system. We can then say that the dimension of such a magnitude is coincident with (or parallel to) the dimension of the motion in the reference system, meaning merely that the quantities are additive. No more than one magnitude (dimension) of such outside motion can be coincident in this manner.

32. KVK: In the calculation of the interregional ratio, how does the factor 8 in 4×4×8 = 128 arise? If we take that the possible number of orientations of the electric displacement as only 8, how to accommodate the greater than 8 displacements in the electric dimension of atoms like 3 3 9 or 4 4 12 etc.?

DBL: The value 12 in 4 4 12 is not a displacement; it is a specific rotation. See page 11, Basic Properties of Matter.

33. KVK: See Reciprocity, VIII (4), p. 25: in diagram A we have, as I have already remarked, 6 displacement units only—not the 8 units between the positive and negative zero points. The natural datum is shown 3 displacement units away from the zero datum. Does ‘zero datum’ mean the stationary reference frame?

See p. 26, top line: “…no effective motion in two of the three dimensions…” Do you mean the dimensions of motion or the dimensions of 3-dimensional space? In the next line you mention that gravitational motion “is an inward motion at unit speed: the kind of a unit in which line (1) of diagram A is expressed.” But line (1) is expressed in speed displacement units. So by the words “gravity is inward motion at unit speed displacement” we find the gravitational speed as 1/(1+1)=½ and not 1. (Moreover, is the gravitational speed of a unit with atomic No. Z equal to 2Z speed displacement units?)

DBL: The comments in Vol. VIII, No. 4, of Reciprocity were a report of reflections on an extemporaneous discussion at the Salt Lake conference of some points that had not been given any extended consideration previously. The conclusions expressed therein were necessarily tentative. More mature consideration indicates that they are not complete, and not as well expressed as they could be. You will find a much better discussion of the subject in Chapter 6, The Neglected Facts of Science. Diagram C in this chapter replaces Diagram A in the Reciprocity article, and Diagram D shows the general relations of the various speed ranges.

34. KVK: See NBM, p. 100, lines 4-6: Independent motion at speed 1/n involves a change of position in 3-dimensional time amounting to 1/n units. Now see the third para, same page. The forward motion of a photon with unit speed is not an independent motion. Only its motion in the dimension of oscillation is an independent motion. As such, how is it that its forward motion (which is fictitious, being only the result of viewing it from our stationary reference system) involves coordinate time, which is utilized to explain the phenomenon of the constancy of the speed of light?

DBL: I am not sure that I understand your point here, but I think that it has to do with my use of the term “independent”, so let me say two things: (1) I am calling any motion other than the outward progression of the natural reference system independent, and (2) the only way in which an independent motion can originate is by means of reversals of scalar direction. Such an oscillating motion is “independent” in my terminology, even though it has components that coincide with the normal outward progression.

35. KVK: When you talk of the possibility of the net speed being 1 - (1/n) , where n is the number of energy units, do you mean that they are natural units of energy? Why is it that energy is taken as space displacement? What is the significance of the minus sign in line (2) of diagram A (Reciprocity, op. cit.)? From line (4) we see that energy magnitudes greater than 4/1 are not possible. What does this mean? What is the equivalent, in ergs, of this 4/1 units of energy?

DBL: (a) Yes. See page 118, The Neglected Facts of Science. (b) Because it is inverse speed; that is, n units of space per unit of time, whereas speed, which we define in terms of the region below the speed of light (unity), is one unit of space per n units of time. (c) When we express the deviation from unity in units, we have to distinguish between the direct units and the inverse units in some way. This is one of the ways in which it can be done. (d) I did not mean to imply that it is possible to attain 4 units of energy, I was merely showing the equivalents. Further study, the results of which are described in Chapter 6, The Neglected Facts of Science, indicates that neither speed nor energy can exceed 2 net units. (e) I have not considered this question at length. Just offhand, I would say that what we are dealing with is one natural unit of energy; that is, unit mass times the square of unit speed, or 1.49×10³ ergs.

36. KVK: Suppose in some case the spatial speed is v cm/sec. (less than light speed, c). What is its corresponding unit in terms of speed displacement? Since v/c = 1/(n+1); n, the number of displacement units = (c/v)-1? And from lines (3) and (4) of diagram A, is a speed v/c equivalent to an energy c/v?

DBL: We can use any appropriate system of measurement, but it is helpful to adapt the system to the particular situation with which we are dealing. In the case of the atomic rotational combinations, it is advantageous to deal with displacements from the natural datum, unity, so that we can express positive and negative magnitudes in commensurate units, and there is no conventional usage that stands in the way of doing this. In dealing with translational motion, on the other hand, we want to examine the effect of successive additions of speed units beginning at zero speed. Measuring from zero in this case is not only convenient for our purpose, but also conforms with the conventional usage. This is why I have substituted Diagram C, The Neglected Facts of Science, for Diagram A in the Reciprocity article. I would recommend that you pay no attention to displacement (measurement from unity) in dealing with translational motion, and express everything in terms of speed (measured from zero speed), or energy (measured from zero energy).

37. KVK: What is the distinction and relation between (a) the positive zero and the negative zero (NBM, p. 153, para 3) on the one hand, and (b) the zero level of the stationary spatial reference system (QP, p. 58, line 6) and the zero motion in time (QP, p. 68, line, 10) on the other?

Also compare QP, p. 97, bottom para and NBM, p. 154, top para. These expositions in connection with the possibility of 8 units, give the impression as though “positive zero” means the same thing as “zero speed in space”. But I understand that

“positive zero” is the speed 1/ l, whereas
“zero speed in space” is 0/1. Further,
“negative zero” is .. .. -1/1 or 1/(-1), and
“zero speed in time” is 1/0.

DBL: The positive zero (NBM 153), the zero level of the spatial reference system (Qp. 58), and zero motion in space are synonymous. Likewise the negative zero, and zero motion in time (Qp. 68) are synonymous. The latter would be the zero level of a three-dimensional temporal reference system.

As I explain on page 119, NBM, I measure speed displacement (usually abbreviated as “displacement”) from unity as a datum level. But I measure speed from the mathematical zero in the usual manner. Just how many units there are between the positive (spatial) zero and negative (temporal) zero depends on the dimensional situation. If we are dealing with the full three scalar dimensions, there are six units between the absolute zero of space and the absolute zero of time. If we are dealing with only one scalar dimension, there are two linear units between the two zeros. But we can resolve this one scalar dimension into three dimensions of space, and then there are eight units (of a different kind) between the two zero points.

38. KVK: I could follow that speeds in the range 1-x pertain to the 3-dimensional space region, and the speeds in the range 2-x belong to the space-time region (the 3-dimensional temporal reference frame because of the second unit status. How is it that the speeds of the range 3-x belong back to the time-space region of the 3-dimensional spatial reference frame?

DBL: What you need here is an understanding of the circumstances under which time acts as “equivalent space”. The second unit of motion, from one unit of speed to two units, is motion in time, as indicated in Diagram B, The Neglected Facts of Science. But since there are six units between the absolute spatial zero and the absolute temporal zero, a two-unit speed is still spatial as a whole. It follows that the motion in time in the second dimension has to act as a modifier of the spatial motion rather than as an actual motion in time. This is the same kind of a situation that we encounter in the atomic rotations. The negative electric rotation of certain atoms is a motion in time (speed n/1), but it does not convert the material atom to a cosmic atom, because the atomic rotation as a whole is still positive. The effect of the motion in time is therefore to modify the motion in space to the extent of its spatial equivalent. The motion in the time region, below unit space, is similar. It is a motion in the spatial equivalent of time, rather than in actual time. The motion therefore remains within the spatial reference system, rather than moving away from it and becoming unobservable, as a motion in actual time would do.

Addition of a third translational unit of speed does not revert back to the same status as the first unit. The motion in equivalent space continues in the dimension shown in Diagram B, but a motion in actual space is added in a second scalar dimension.

39. KVK: What happens to the inverse thermal motion of a cosmic atom during ‘scalar inversion’ (that is, entry from the cosmic sector into the material sector). Since thermal motion in our sector is a linear vibratory space displacement, the inverse thermal motion of the sector should be a linear vibratory time displacement. As such, how does this linear vibratory time displacement dissipate or show up in our environment?

DBL: Radiation frequency is a speed; that is, cycles per second 1/t, is actually units of space per second, s/t. The effective unit of wavelength is about 10^-3 cm. Radiation at shorter wavelengths is motion at speeds above unity (displacement in space). This includes the near infrared, the optical region, and the ultraviolet—that is, the bulk of the thermal radiation—as well as x-rays and gamma rays. The inverse thermal radiation occupies a similar range on the long wavelength side of 10^-3 cm: the far infrared and the radio range. These are speeds below unity (displacement in time). Astronomical radio emitters are usually also strong sources of infrared radiation (inverse thermal).

40. KVK: The frequency of the H.F. radiation is greater than one, say, n/1. This means that there are n space units associated with 1 time unit. This means that it is the time component that is alternating between inward and outward directions. Now if it is the space unit that is so alternating (as in the L.F. radiation), this appears as an oscillation in space from the point of view of the stationary 3-dimensional reference frame. But if the alternating unit is time unit, how do we (from the stationary reference frame) see it, still as a vibration in space, or as a vibration in time? Please note that I am not asking about the forward movement of the photon in the perpendicular dimension at all. I am asking about the motion in the dimension of oscillation.

DBL: In all cases we see one space unit in the reference system, and we have to measure the time on a clock, There is no way in which we can distinguish observationally between a space-time ratio of 1/n and one of n/l. If we want to know the frequency corresponding to unit speed, we have to calculate it.

41. KVK: Have the following been worked out in the context of the RS: (a) The relative cosmic abundances of the elements; (b) nuclear isomerism—origin and explanation; (c) radiation emitted due to the electron spin changing direction, for example, the 21 cm. radiation from hydrogen. How does ‘spin’ fit in our theory? (d) explanation of the origin and the characteristics of the cosmic background radiation (NBM, p. 175).

DBL:

1. This has not been studied, so far as I know.

2. I do not know of any studies made on these items either,

3. The electron does “spin”; that is, it rotates, but I doubt if the accepted explanation of the origin of the radiation is correct.

4. This is undoubtedly the radiation from the cosmic sector. We have the explanation for the origin and for the principal characteristic—the isotropy and the intensity (which we can explain approximately). I do not believe that it is worth while trying to go any farther at this stage of the theoretical development.

42. KVK: Gravitation is a rotationally distributed motion, its direction being redetermined after the end of each (natural) unit of time, since it is inward. In the long run, this results in its being distributed in all directions of 3-dimensional space, by probability. But suppose there is the intervention of an external element, which introduces a preferred direction—such as by rapid spinning—does the gravitational motion get directed in the direction of the spin axis in space more often than in the other directions, producing in the long run, ‘directed gravity’? Does the spinning of an object produce space displacement?

DBL: According to my findings, gravitation is a continuous, uniform, rotationally distributed scalar motion at unit net inward speed, and cannot be anything different. An external force cannot change the inherent characteristics of this motion. It simply imparts a vectorial motion to the gravitational combination of motions.

43. KVK: What is the difference between the inner and the outer gravitational limits (QP, p. 166)? At the outer gravitational limit, the gravitational motion due to the entire mass aggregate becomes unity and beyond it becomes zero as fractional units do not exist. But what happens at the inner gravitational limit, where the inward motion due to gravity equals the outward motion of the progression? Here too, since the outward motion due to the progression is unity, is not the inward motion due to the gravitation also one unit, if both these are to be equal?

DBL: At the gravitational limit the inward motion of an aggregate of m units of mass is m units. The outward motion is likewise m units, and the net speed is zero. Beyond this limit the gravitational motion decreases with the distance, and has the value m-x. When m-x = 1, any further increase in the distance drops the gravitational motion to zero, as there are no fractional units. As can be seen from the foregoing, the outward motion at speeds less than unity, such as the galactic recession, is purely a phenomenon of aggregates. In the case of a single isolated unit of mass, the gravitational motion would drop to zero at the gravitational limit; that is, the two limits would coincide.

44. KVK: If gravitational effect decreases as 1/d², how does one obtain the linear relation of Hubble’s distance vs. speed?

DBL: The inverse square relation applies where the distribution is three-dimensional. Beyond the gravitational limit (unit gravitational speed) the distribution is two-dimensional.