Reproduced below are comments on D. B. Larson’s Nothing But Motion (NBM) and New Light on Space and Time (NLST) interspersed with responses by the author. The correspondence from which this dialogue is excerpted took place c. 1980.
- KVK: p. 156, 13th line from bottom, NLST: Instead of the words “basic vibrating unit” it must be “rotational base.”
p. 123, 10th line from bottom, NBM: in “However, the rotational displacement… ,” the word “rotational” should be replaced by “vibrational.”
DBL: You are right on both of these items. I have expressed the first one in the correct manner on page 140 NBM.
- KVK: There is a difference in the notations used for representing the rotations of atoms (e.g.: 2-1-0, p. 236, NLST) and of the sub-atomic particles (e.g.: 1-0-(1)). In the former the numbers represent double natural units whereas in the latter they represent single natural units. This divergence is a source of confusion as no attempt was made to clarify it, and both modes of notation were used at the same places, as in p. 236, NLST.
DBL: I gave a brief explanation on page 231 NLST, but this book is, as I said in the preface, a “bird’s eye view,” and I could not go into much detail on anything. There is a more extended explanation on page 140 NBM, including setting up a new system of notation to avoid the difficulty that you point out. I do not believe it advisable to try to use the same notation for both atoms and sub-atomic particles, as this would lead to complications in the development of the theory.
- KVK: p. 170, last but one para, NLST: It is not clear how a proton, M 1-1-(1), can acquire a positive electric charge (see p. 145, NBM). From what has been explained in the para cited above and elsewhere, as its electric rotational displacement is space-like, the proton can only acquire a negative electric charge—like the electron.
DBL: An electric charge is a one-dimensional rotational vibration. In order to be stable and identifiable as a separate entity it must oppose the rotation with which it is associated, but this does not have to be the rotation in the electric dimension. The charge can oppose the rotation in one of the magnetic dimensions. Since the magnetic rotation is always positive in the material sector, this means that all material elements can take positive electric charges under appropriate conditions. In fact, at high temperatures, such as those in the stars, all elements are positively charged.
- KVK: On p. 155-6, NLST, the apparent reduction in the velocity of light in a material medium is attributed to the additional space involved due to the rotational space-like displacements included in the structure of most atoms of matter. On this score, the apparent velocity of light in a material medium with only positive rotational displacements should be greater than c!
DBL: I am not quite clear as to the point of your comment. I will say, however, that ordinary matter is a time structure; that is, one in which n units of time are associated with each unit of space (as we see the situation in the context of the conventional fixed system of reference). When the photon passes through this matter, the total time involved in the motion is increased by the addition of the time component of this matter. The photon speed, the ratio of space to time, therefore decreases. Conversely, in the cosmic sector, where matter is a space structure, the speed of light is increased in passing through cosmic matter.
- KVK: Speaking of the progression of the photon in the free dimension it is remarked that “… the combination of a vibratory motion and a linear motion perpendicular to the line of vibration results in a path which has the form of a sine curve.” (p. 51, NBM) In the case of HF radiation, the space component of the vibration progresses unidirectionally while it is the time component that oscillates back and forth. As such “the linear motion perpendicular to the line of vibration” referred to above cannot be the scalar progression of the space component of the general space-time progression. Is the sine curve form, then, taken to be pertaining to the three-dimensional time?
DBL: The frequency of the radiation is irrelevant. In either case, HF or LF, the progression of the natural reference system in the dimension of the vibration is neutralized by the reversals. This permits a progression to take place in a perpendicular dimension. The scalar motion (progression) in this second dimension is totally independent of that in the first, as scalar quantities cannot be combined vectorially.
[KVK: Apparently, my question was not clear here. What I meant was: a progressing sine wave has two components—(i) the oscillation in the lateral dimension and (ii) the uniform forward progression. Now my point is, that both these components must be of the same nature—either spatial or temporal. Thus, if the oscillation component is in time, the progression component in the perpendicular dimension to be compounded with this has to be in time also; and the sine wave must be envisaged as occurring in three-dimensional time and not in three-dimensional space.]
- KVK: Explaining the effect of adding rotation to the vibrational units of a photon, it is said that the “remaining vibrational units of the original photon continue as a photon of lower displacement” (p. 123, 3rd para, NBM). But it is not clear how the detachment of one of the vibrational units (which are anyway discrete) reduce the displacement of the original photon.
DBL: The units that I am talking about here are units of displacement—that is, units of speed. (See explanation of the use of the term “displacement” on pages 119-121 NBM.) When one unit is detached to join the rotational motion, the photon continues on its way with one less unit of speed (a lower frequency).
- KVK: The liquid state is the result of vanishing of the force of cohesion in one dimension (and the gaseous state in three dimensions). However, whether the vanishing of the cohesion in two dimensions results in any specifically observable distinction is not made clear. Is it to be equated to the vapor state?
DBL: Probably. I had not covered this subject fully twenty years ago when I interrupted my research work in order to start publication of my results, and I have not been able to get back to it since. My conclusions in this area are therefore somewhat tentative.
- KVK: p. 173, top para, NLST: Not only this—if the hypothesis of the tendency of atoms to assume a stabler structure like that of inert gases by gaining an electron is true, should not the atoms, say, of chlorine, tend to transform to those of argon, if placed in an environment of negative electrons, by absorbing single electrons?
DBL: It looks that way to me, too, but I suppose we will have to let the supporters of conventional theory answer this question.
- KVK.: p. 50, bottom para, NBM: It is not clear why do the inward/outward scalar reversals result in vectorial direction reversal in only one dimension? Why they do not produce a three- or two-dimensional vibrating unit?
DBL: We are dealing with a scalar motion, and the only latitude that we have, at this stage of the step-by-step development, is to change from + to - and vice versa. This does not necessarily preclude introducing additional dimensions of motion later in the development, but multi-dimensional scalar motion has some unfamiliar features. I intend to discuss this type of motion at considerable length in Volume II.
- KVK: p. 195-6, NLST: In view of the dimensional differences in the origin of electrical, magnetic and gravitational forces which are actually motions of the same general nature, it is shown that the force exerted by an electric charge on an uncharged mass is only 1/c2 as great as the force on an object with a charge of comparable magnitude. However, no mention is made of the force exerted by the electric charge on a magnetic charge, which, though it must be less than the force of an electric charge on electric charge, must, nonetheless, be greater than the force exerted by electric charge on uncharged mass. Hence this must be within the possibility of detection, like the weak force exerted by a magnetic charge (referred to in the para cited) on a (magnetically uncharged) mass unit.
DBL: I have not arrived at a firm conclusion on this point as yet. It had occurred to me, and I have given it some consideration. So far, I am inclined to believe that it will be ruled out by the directional orientation of the electric and magnetic forces.
- KVK: Within the gravitational limit of a material aggregate there is net inward scalar motion. As such, what would happen to a photon emitted from the object, within the gravitational limit? As the photon has no independent motion but is only carried away by the general space-time progression and since the net motion now is inward , how can we account for the velocity, c, of the photon and its eventual emergence from the domain of the gravitational limit?
I think, the argument that the above net inward motion within the gravitational limit belongs only to the material aggregate and does affect the photon is not valid. Even if such an argument is preferred, it raises another difficulty: how to account for the bending of light rays in a gravitational field gradient.
DBL:
- KVK: The massless sub-atomic particles do not have net time-like displacement in three dimensions like the atoms. As such why are they not carried away by the general space-time progression, since inward gravitational motion is not present to counteract the outward scalar progression? Doubtless, they differ from the photons thus carried away by the space-time progression in having additionally rotational displacements. But so long as the net rotational displacement is in less than three dimensions, the space-time progression should carry it off in the free dimension. Perhaps this could be the reason that this class of sub-atomic particles is not observed (p.142, NBM). It is put forward that the uncharged electron, for example, cannot move through space as its net displacement is space-like and the relation of space to space is not motion. However, since the one unit of two-dimensional rotation is balanced by the unit of negative vibration, and the net space-like rotation is only in the electric dimension, is there no dimension effectively free so that the scalar space-time progression applies in that dimension?
DBL: These massless particles undoubtedly move at the speed of light, as you suggest. Our inability to observe them is not due to their speed, but to the fact that, except in the case of the neutrino, we have not, thus far, identified processes in which they take part. Experience with the neutrino suggests that some of the effects of the other massless particles may also be detectable if we look in the right places.
- KVK: Instead of a RV1 displacement being added to an existing rotational displacement as in the case of atoms, is it possible to have a rotational vibration (of opposite space-time character) directly added to the linear vibrating unit that is a photon? For example, a negative electric charge, RV1-, can be imposed on a photon, LV1+?
DBL: No. A charge is a rotational vibration. As such, it can only exist as a modifier of a rotation. Otherwise there would be nothing to constrain it into the rotational path, and it would revert to the status of a linear vibration.
- KVK.: Chapter 13, NLST: The discussion does not bring out some important aspects of the difference in the characteristics of electric and magnetic charges compared to those of gravitation.
Firstly: Like electric charges repel each other and unlike charges attract. In order to explain this should it be taken that the scalar effect of the charge is both inward and outward in space-time at the same time?
Secondly: The gravitational force, unlike that due to charges, cannot be screened off (p. 60, line 3, NBM) because gravitational motion is inward scalar motion with respect to the general structure of space-time. Now if, the motion which gives rise to the electric or magnetic forces is a motion of the same general nature as that of gravitation, being the motion of the individual atom or particle with respect to the general structure of space-time (p. 186, NLST), it is difficult to see how these forces can be screened off as is possible actually.
As regards the first point the following line of explanation may be considered. The negative electric charge, being a time-like RV displacement, must have an attendant scalar translational motion in space (just like the gravitational motion of a positive rotation). Like the positive rotation, it may appear that this RV displacement should therefore involve a scalar inward motion in space. However, “… because of its vibrational character each unit of this charge is only half as effective as a unit of unidirectional rotation.” (p. 190, NLST) Consequently, this accompanying scalar translational motion is midway between the general outward space-time progression and the inward scalar translational motion of a rotational unit. Thus it appears as a scalar outward motion in space from the point of view of the gravitationally-bound stationary reference system. This manifests as mutual repulsion between the negative electric charges.
On the other hand, the rotational vibration that is a positive electric charge, is a space-like RV displacement. Hence it involves a scalar translational effect similar to that of a unidirectional rotation that is space-like (motion in time). But the scalar translational motion of space-like rotational displacement units (i.e., rotation in time) is the gravitation in time. As such the space-like RV displacement too involves a scalar inward motion in time. Once again, as in the previous case, because of the fact that the vibrational rotation is only half as effective as a unidirectional rotation, this attendant scalar inward motion in time of a positive electric charge falls midway between the general outward space-time progression and the inward gravitational motion in time. Now, in order to understand how this appears from the point of view of the stationary spatial reference system, we must recall that in the context of such a reference system, the progression of the time component is the same as that in the natural reference system. Consequently, the scalar translational motion of the positive electric charge is apparent as inward in time. This manifests itself to us as mutual repulsion of the positive charges, since the inward scalar motion in time is tantamount to outward scalar motion in space.
Finally, the relationship of negative to positive electric charges is that of scalar outward motion in space to scalar inward motion in time and manifests to us as mutual attraction of the positive and negative electric charges.
Regarding the possibility of screening off the electrical charge effects: once we see them as basically scalar motions of the individual charges, screening becomes impossible, like in the case of gravitation. The following interpretation may be relevant. The screening is a balancing of the inward (or outward, as the case may be) scalar motion by a vectorial motion (i.e., “co-ordinate” as versus “clock” motion) in the dimension (or dimensions) concerned, by the screening object. This characteristic of the screen, the generation of motion oppositely directed to that of the scalar translational effect of the charge is not unlike the process of acquisition of gravitational charges due to captured charged neutrinos.
As given, since “… the natural unit equivalent of a magnetic (2-dimensional) displacement n is 4n2… ,” i.e., (2n)2 , the natural unit equivalent of a magnetic displacement unit of 1 is 22 = 4, and in equivalent electric units is 4/2 = 2 (in view of the double units we are working with). On the other hand, the natural unit equivalent of the magnetic displacement unit of Ö1 is (Ö2)2= 2 and in equivalent electric units is 2/2 = l. Thus, it does not seem to matter, at unit level, whether we consider the first unit of magnetic displacement as 1 or Ö1, only the latter is actually relevant, since this alone gives us the correct atomic number sequence.
This important point is not brought out in the discussion and the whole issue is glossed over with nothing more than one sentence, “At the unit level dimensional differences have no numerical effect, i.e., 13 = 12 = 1.” (p. 128, NBM).
Indeed, the role of unity, as a natural datum, is of far-reaching significance. The requirement of the first effective unit of the 2-dimensional displacement being Ö1 instead of 1 can be seen to be arising out of the following. The first unit of displacement, from the rotational base, has a unique and distinguishing characteristic in that it marks the emergence of “something physical compared to the prevenient nothingness.” Inasmuch as this is so, the difference between the first unit and the rest is not only one of degree—but something else besides. The addition of the first displacement unit involves a transit from the region inside the unit displacement to that outside. Hence the dictum that “… all of the physical phenomena of the inside region… are… second power expressions of the corresponding quantities of the outside region” (p. 155, NBM) applies here. Consequently, the 1 unit displacement, when looked at from the viewpoint of physical manifestation—i.e., from the “somethings” side of the unit boundary as against the “nothings” side—is to be regarded as Ö1.
It must be noted that the setting up of units and measurement procedures from the standpoint of the natural reference system, in terms of speed displacements results in the relation between the algebra of displacements and the algebra of the conventional speed units being exponential in nature. This is to say that the addition of displacements is equivalent to the multiplication of the corresponding speeds.
Suppose we define the speed displacement d, of a speed v, as d = 1g c - 1g v, since it is a deviation from the unit speed, c; all speeds like 1/n give positive displacements, lg n, while speeds like n give negative displacements, -1g n, and unit speed c gives zero displacement, 1g 1. Though this definition does not exactly tie in with the treatment in the book, it nonetheless serves to demonstrate the general exponential nature of the relationship mentioned above. It also illustrates how the addition of a motion of (n-1) positive displacement units to another of (n-1) negative displacement units produces zero displacement (p. 121, NBM), since in dealing with the corresponding speeds we need to multiply the speed n (represented by (n-1) negative displacement units) by speed 1/n ((n-1) positive displacement units) to obtain the unit speed (zero displacement).
DBL: Your criticism of the lack of coverage of electricity and magnetism is valid, but here again you should bear in mind that a “bird’s eye view” does not see everything. I will give you a much broader view of these subjects in Volume II of the new edition.
As brought out in Volume I (particularly in Chapter 18), linear motion is limited to two full units, from +1 to -1, as seen in our fixed reference system. In terms of the natural reference system both +1 and -1 are zero, the + zero and the - zero, we may say, if we look at the situation from the standpoint of what is happening in the region between the two. The motion of an electric charge is always outward, but the motion of a positive charge is outward from the positive zero, while that of a negative charge is outward from the negative zero. Two positive charges move away from each other, as shown in the upper tine of the diagram below. Two negative charges also move outward away from each other, as shown in the lower line. But a positive charge and a negative charge move toward each other, as indicated by the middle line, even though they are both moving outward from their respective zero points.
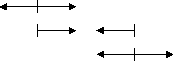
- KVK: Regarding the lifetimes of the cosmic decay particles (Ch. 15, NBM) the following points may be considered. The spatial extension of the cosmic atom is the analog of the lifetime of the atom in the material sector. As such the lifetimes of the decaying c-atoms must bear a relation to their spatial extensions before the decay.
The correlation of lifetimes with the dimensions shown in p. 192, (NBM), can be arrived at by tying together some loose ends as below (with appropriate interchange of the words “space” and “time”):
- The limiting spatial extension of the incoming atom in each dimension is one natural unit (i.e., s in conventional units). Thus the extension space involved in two dimensions becomes s2, and in three dimensions, s3.
- The temporal equivalent of this spatial extension s is s/c.
- “..If the motion is one-dimensional, all of the effects can be transmitted. If it is two-dimensional, the fraction transmitted… is 1/c of the total… The transmitted fraction is only 1/c2 in the case of three-dimensional rotation.” (p. 185, NLST)
- “… The time region speed, and all quantities derived therefrom, which means all of the physical phenomena of the inside region… are… second power expressions of the corresponding quantities of the outside region.” (p. 155, NBM)
The Table below shows the result of applying these criteria (i) to (iv) above to the various dimensional motion.
Criterion No. Number of Dimensions 1 2 3 i s s2 s3 ii s/c s2/c s3/c iii (s/c) (s2/c)(1/c) (s3/c)(1/c2)
iv (s/c)½ [(s2/c)(1/c)]½ [(s3/c)(1/c2)]½ Result in secs. 1.233148×10-8 1.520655×10-16 1.875193×10-24 On the other hand, if the extension space involved in the two- and three-dimensional cases is respectively p/4s2 and p/6s3 (based on statistical circular and spherical symmetry in co-ordinate space) instead of s2 and s3, we have the calculated values of the lifetimes in the two- and three-dimensional cases as respectively 1.347645×10-16 and 1.356892×10-24 seconds.
DBL: You may have something here. I do not have time to make a full evaluation of your proposal now. In fact, I have a general policy of not making a quick decision on any new idea, whether it is my own or comes from someone else. But it appears to me that this may be the kind of a thing that I was looking for (unsuccessfully) at the time I wrote Chapter 15. I suggest that you prepare a paper on this subject and send it to Professor Meyer for publication in Reciprocity, so that the NSA members can take a look at it.
-
KVK: The general space-time progression of our universe is an outward scalar progression. How is this to be distinguished from one with both space and time progressing inward? The universe of motion with both space and time progressing outward is indistinguishable from that with both space and time progressing inward. In addition, both these cases are indistinguishable from a third case where for one unit both space and time progress outward and in the next unit both of them progress inward, alternately. It is not clear how this indistinguishability is built into the conceptual framework of the theory. Moreover, how (or whether) our consciousness has come to regard it as an outward progression is not evident.
DBL: The existence of a physical universe is possible only if gravitation is inward, so that the originally widely dispersed units of matter move closer together and eventually reach positions in which they can interact. This means that the arbitrary fixed reference system that we set up on the basis of such interactions is moving inward relative to the natural reference system. The apparent progression of the natural reference system is therefore outward.
-
KVK: “… deviations from unit speed… are accomplished by means of reversals of the direction of the progression of either space or time.” (p. 75, NBM) What about the case of conjoint reversals of both space and time, like: -s/+t , +s/-t , -s/+t… etc.? That is, for one unit space progresses inward while time progresses outward. In the next unit space progresses outward and time progresses inward. Such a basic motion has a speed of -1 that is unvarying and must be both an independent and a stable motion. Can we identify the above “coupled-vibration” with any physical entity? The above may even result in rotation. At any rate, the motion is similar to the inward translational aspect of the material gravitation.
DBL: A speed of unity, 1/1, is no motion at all relative to the natural system. We cannot distinguish between no motion in space and no motion in time.
[KVK: But reply does not answer the point I raised here. I was asking whether this “coupled vibration,” with speed of -1 like the gravitational motion, could be realized in some physical entity?]
-
KVK: I find that the following concepts are not explained adequately, with the result the reader (who is being exposed the first time) is left with many nagging why and hows:
- the inter-regional ratio (p 154, NBM)
- secondary mass (p. 161, NBM)
- electric mass and mass of electric charge (p. 163, NBM)
- secondary neutral valence
DBL: I am not sure just what you have in mind here. Are you merely suggesting that I should explain these points more fully in later publications? (in which case, I thank you for the suggestion), or do you have some questions that you want answered? (in which case I would like to have something more specific).
- KVK: p. 100, NBM: Continuing the line of argument (in the text), if we substitute an object with a speed less than c for each of the photons, instead of for only one (as suggested in the last-but-one para), we arrive at the true relative v speed of the two objects as (v1+v2)/(v1+v2) = 1 always. Thus the true relative speed always turns out to be unity for any objects—not necessarily only for photons.
DBL: The time component of speed always includes the time of the progression (clock time), regardless of whether the moving objects are, like the photons, moving at the unit speed of the progression, or at some different rate. Thus the denominator is always 1 / v, never v alone.
[KVK: Does the answer here mean that the relative speed of two objects with speeds v1 and v2 (in natural units) is given by (v1+v2)/(1+v1+v2) since the total time involved would be (1+v1+v2)?]
- KVK.: 128-9, NBM: It is not clear why the relation that “… a magnetic displacement n is equivalent to 2n2 electric displacement units” does not hold good for n=1. For n=1, the equivalent electric displacement works out to be 2, by this formula. However, in the development of the series of elements, the magnetic displacement 1 is counted as an equivalent electric displacement of 1 unit and not 2. There is definitely a hiatus in the reasoning here, an examination of which may lead to some important insight and clarify, among others, the case of half units represented in M ½-½-0, for example.
Under these circumstances, it is not difficult to see that halving the displacement unit amounts to taking the square-root of the corresponding speed and does not involve any half unit of speed (i.e., if d = 1g n, then ½d = ½1g n = 1g Ön). For particles below the unit level, as in the case of sub-atomic particles, this gives rise to the unique possibility of positing ½ unit displacement (141, NBM) because of the idempotent nature of unity (i.e., Ö1= 1), without involving anything less than unit speed.
DBL: I don’t believe that I get the point of your argument on this item. So far as I can see, we are applying the same relation all the way through the series of elements. The sequence of magnetic additions is this:
Rotation Net speed Electric Equiv. Rotational base (2) 1-0-0 0-0-0 Effective zero (unity) 1-1-0 1-0-0 } n=1 Helium 2-1-0 1-1-0 2 Neon 2-2-0 2-1-0 10 } n=2 Argon 3-2-0 2-2-0 18 We start with a rotational base for each of the two rotating systems of the atom, with net speed zero in all dimensions. Then we add one magnetic rotational unit to bring the effective speed to unity, the natural zero level. (The language that I used in the book may have been somewhat misleading, although I did say specifically that the purpose of this first magnetic unit is to bring the scalar speed to zero on the natural basis.) Since this non-effective unit uses up one of the n = 1 spots, there is only 2 × 12 group of elements, and a 2 × 22 group follows, as shown in the tabulation.
- KVK: p. 154, NBM: The inter-regional ratio is calculated on the basis that “for each of the 128 possible rotational positions there is an additional 2/9 vibrational position… ” The ratio is thus found to be 128(1+2/9) = 156.44. However, in the case of sub-atomic particles, which are single rotating systems, only one, and not two, of the possible nine vibrational positions are occupied. Thus the inter-regional ratio must be 128(1+1/9) = 142.22 and not 156.44.
DBL: You are correct. The 142.22 ratio must be substituted for 156.44 in the appropriate applications. I said this on page 163 NBM.
This completes the items that I received from Professor Meyer. I have tried to be responsive to the questions that you have asked, but it cannot be expected that all of my answers will be satisfactory. So I want to assure you that I will be glad to discuss any of them at more length if there are issues that you want to raise. It is apparent from your comments that you have gained a good deal of insight into the structure of the theory already, and I would like to help clear away any obstacles that still remain in the way of a full understanding.
It has become quite clear since publication of Nothing But Motion that the scientific community in general has very little comprehension of the scalar type of motion that plays such a large part in my theoretical development, although scalar motion is not something that is peculiar to my theoretical system. It is something that exists as one of the phenomena of the physical universe, and any physical theory should be prepared to deal with it. Since it is a very important factor in my theoretical structure, and so generally neglected in current practice, I am planning on including an extended discussion of this type of motion in Volume II. I put a part of this discussion into a memorandum that I used at the recent NSA conference at Huntsville, Alabama. I believe that this should be of some interest to you, and I am therefore enclosing a copy.
