Part I: The Nature of Stellar Matter
1 Introduction
Larson has discussed the development of the Reciprocal System of Physical Theory to a great extent in his two works, Nothing But Motion1 and The Universe of Motion2, the latter work especially dealing with the astronomical applications. Stars are the basic building blocks of the large-scale universe. As such, the knowledge of their internal constitution and dynamics constitutes an important step in the understanding of the macroscopic universe. Larson developed the general structure and the details of evolution of the stars of various types.2 The detailed study of their internal structure has not yet been carried out in the context of the Reciprocal System. Therefore, such a study was taken up as an initial attempt to fill this gap and some of the results obtained are reported herein.
In Part I, we will discuss the general properties of matter at very high temperatures, applying the principles and concepts developed by Larson in his works cited. Since the sun is the only star about which a wealth of observational information is available in great detail, an attempt is made to explain some of the solar phenomena—phenomena so well known but whose nature is by no means clearly understood by the scientists—utilizing the conclusions reached in Part I. This is reported in Part II. It is hoped that these will be found interesting to the researchers of the Reciprocal System and stimulate further investigations.
According to the Reciprocal System, the energy generation in the stars is by the atomic disintegration process.3 Larson shows how the operation of this source at the central regions of the stars gives rise to a fluctuating energy output, its periodicity showing up even in the case of the stable stars, though not as conspicuously as in the case of the intrinsic variables. Thus, he attributes the 11-year periodicity of the sun to this fluctuation of the internal energy generation.4
The basic scalar motion that constitutes the material atoms is a speed displacement in time. Both the thermal motion and the electric charge of the atoms are displacements in space. At a large enough temperature, called the thermal destructive limit, the combined space displacement due to the thermal motion and the positive electric ionization is sufficient to neutralize one of the rotational time displacement units constituting the atom and reduce it to the linear status (radiation). Preliminary calculations indicate that the thermal limit of the elements is greater than two natural units of temperature.5 Accordingly, the material in the central region of a star has to be at temperatures beyond the unit level, and this gives rise to significant results as explained below.
2 Discovery of a New Source of Magnetism
Larson refers to the speeds in the range of one to two natural units as the intermediate speeds, and those above two units as the ultra high speeds. In a similar manner, we will refer to the temperatures greater than one natural unit, but less than two natural units, as intermediate temperatures, and those beyond as ultra high temperatures. In addition, we will call the temperatures below the unit level as the low temperatures. This connotation of “low” will be used throughout our discussion, and must be so remembered.
In the intermediate range, the motion is in time instead of space. However, where the net total motion is still in space, the motion due to the intermediate speed component will be in the space equivalent of time, that is, in equivalent space.6 As such, the effects of the thermal motion when the temperature is in the intermediate speed range, are in equivalent space, rather than in the space of the conventional reference system. An important, direct consequence is that this thermal motion would be two-dimensional, as is all motion in equivalent space.7
In view of the fact that both the thermal motion, and the motion constituting the positive electric charge, are of the same type—namely, one-dimensional vibratory space displacements (except that the former is a linear vibration, and the latter is a rotational vibration), thermal motion readily engenders electric ionization when present in sufficient intensity. This thermal ionization, of course, is a known phenomenon.
In a similar manner, the thermal motion in the intermediate range, being of a two-dimensional linear vibratory space displacement, readily produces on the basic units of matter present, a two-dimensional rotational vibration, with space displacement. We can immediately recognize that the latter, namely the two-dimensional rotational vibration with space displacement, is nothing but the magnetic charge! Thus, throughout the stellar interiors, where the thermal motion is above the unit level, magnetic fields of intensity proportional to the strength of the thermal motions are always generated.
Instead of relegating the role of the magnetic fields as minor, we now find that the presence and configuration of these thermally generated magnetic fields largely determine the structure and dynamics of the stellar phenomena. Since the interiors of all stars have to be at temperatures above the unit value if energy generation by thermal destruction is to take place at all, intense magnetic fields must invariably be present in all of them. This does not, however, mean that these fields reach up to the stellar surface in their full intensity. Only few field lines seem to penetrate through the outer bulk of material that is at lower (that is, less than the unit) temperature, as we will see later. While fields as strong as 10,000 gauss might be generated at the core, the surface field may be of the order of tens of gauss to a fraction of a gauss.
3 Nature of the Matter and Radiation at Very High Temperatures
We will now summarize some important conclusions reached by Larson, and add our own discussion to their further implications concerning the states of matter and radiation at the upper range speeds.
3.1 The Radiation Intensity
“… thermal radiation originates from linear motion of the small constituents of the material aggregates in the dimension of the spatial reference system. The effective magnitude of this motion is measured as temperature.
“Inasmuch as motion at intermediate speeds is in the same scalar dimension as the motion at speeds below unity, the vibrational motion that produces the thermal radiation continues into the upper speed ranges. But because of the reversal at the unit speed level, the temperature gradient in the intermediate region is inverse; that is, the maximum intensity of the thermal vibration, and the resulting radiation, is at the unit speed level, and it decreases in both directions.”8
In the intermediate region, an increase in temperature (equivalent to a decrease in inverse temperature) decreases the thermal radiation.
As a consequence of this, if we try to identify a thermal source at the upper end of the intermediate temperature range by observing the intensity of its radiation, it would appear to be at a low temperature, of an order that is not beyond the ken of terrestrial experience.
A further fact of significance is that, “…all radiation from objects with upper range speeds… is polarized as emitted. Where a lower polarization is observed, this is due to depolarizing effects during travel of the radiation. A three-dimensional distribution of radiation is impossible in a two-dimensional region.”9
3.2 The Inverse States of Matter
3.2.1 Radiation Spectrum
“Furthermore, the radiating units of matter are confined within one unit of time, at the upper end of the intermediate temperature range (the lowest inverse temperatures), just as they are confined within one unit of space at the lower end of the normal temperature range.”10 “The physical state of this material is the temporal equivalent of the solid state: a condition in which the atoms occupy fixed positions in three-dimensional time, and the emission is modified in the same manner as in the solid state.”9 This radiation has a continuous spectrum.
3.2.2 Analogy Between the Phenomena of the Time Region and Those of the Space Region
Corresponding to the three states of matter in the low temperature range—solid, liquid, and gaseous—there ought to be three more states in the intermediate temperature range, which we may call the inverse gas, the inverse liquid, and the inverse solid, in that order of increasing temperature (decreasing inverse temperature).
In order to see how the effects of motion in the space region (occurring at the far end of the intermediate speed range) manifest themselves to observation in the time-space region (the conventional three-dimensional, spatial reference system), we will first consider how the effects of motion in the time region are known to manifest in the time-space region, and then draw an analogy. We can tabulate:
|
Motion Originating |
Effects as manifested in the conventional reference frame |
|---|---|
|
In the time |
|
|
|
|
In the space |
|
|
An example of the time region phenomena is the crystal or grain of the solid state—which is of limited spatial extent, but exists continually in time. In the case of the space region phenomena, in view of item No. (iii) tabulated above, the spatial aggregations of the atoms concerned do not persist continually: they keep forming and dissolving into fresh, new aggregates.
3.2.3 The Lifetimes
The lifetimes of these space region aggregates, that is, the times elapsed before they dissolve to give place to new aggregates, depends upon the rate at which the heat transfer is taking place. In the case of solidification from liquid to solid state, a high heat transfer rate produces smaller grain size (more number of grains per unit of space). In the case of the inverse states we are considering, this should result in less number of “grains” per unit of time. This means that the lifetimes are longer with higher heat transfer rates.
3.2.4 The Spatial Configuration
The motion in time has no direction in space, and does not manifest as a movement of individual atoms, as such, in space. However, there are some observable effects on aggregates of atoms. For instance, the scalar direction of thermal motion is always outward. The expansion in time resulting from the intermediate temperature shows up as a contraction in equivalent space. Or conversely, if matter at the upper temperature ranges is cooling to the low temperature region, we would expect it to expand. We will have occasion to refer to this phenomenon in the context of sunspots, later.
3.3 Thredules: the Seventh State of Matter
We have seen how the intermediate range temperatures give rise to three more states of matter—the inverse states, as we are calling them—in addition to the three known states pertaining to the low temperature range. The entry of the temperature into the ultra high range, beyond the two-unit limit, results in a yet another, seventh, state of matter.
The third unit of motion is already beyond the two-unit limit of the dimension of scalar motion that is coincident with the dimension of the conventional spatial reference system. It pertains to a second scalar dimension incapable of representation in the conventional reference system.
But:
“…some of the change of position due to the unobservable ultra high speeds is represented in the reference system in an indirect manner… the outward motion of the ultra high speed… is applied to overcoming the inward gravitational motion…. Inasmuch as that gravitational motion has altered the position (in the reference system) of the matter…, elimination of the gravitational motion results in a movement of this matter back to the spatial position that it would have occupied if the gravitational motion had not taken place. Since it reverses a motion in the reference system, this elimination of the gravitational change of position is observable.”11
“Thus, even though the speeds of the particles… are in the ultra high range, the observable thermal effect is in the low speed range, and the radiation that is produced has a line spectrum like that of an ordinary hot gas.”9
“Inasmuch as the spatial motion component of the ultra high speed motion is in a second scalar dimension, it is perpendicular to the normal dimension of the reference system. This perpendicular line cannot rotate in a third dimension because the three-dimensional structure does not exist beyond the unit speed level. Thus the representation of the motion in the reference system is confined to a fixed line…”
“…this type of motion does not distinguish between the direction AB and the direction BA, since the only inherent property of the motion is a magnitude… any linear motion originating at a given point is therefore divided equally between two opposite directions by the operation of probability.”12 The matter at ultra high temperature, therefore, takes the shape of a sheaf of expanding rectilinear threads. We will call these unidirectional filaments ‘thredules.’ There is ample observational evidence of this slender, thread-like structure associated with the ultra high speeds like in the cases of the remnants of Type II supernovae,13 and quasar explosions.14
Before passing on to the next section, we must mention that since beyond the unit temperature the magnetic field is a concomitant phenomenon, we find that every thredule is invariably associated with magnetic flux lines running along its longitudinal axis.
4 Magnetism and Co-Magnetism
In Section 2 we have seen how the upper range temperatures generate magnetism. The basic motion constituting this magnetic charge is a two-dimensional space displacement of rotational vibration type, and so is the same as that of a magnetic charge in the material sector, in general. However, the fact that the thermally-generated magnetism we have been considering occurs in equivalent space, rather than the space of the conventional reference system, introduces a new element into the situation that produces some unfamiliar effects as viewed from that reference system.
4.1 The Lines of Force
It is usual to try to understand the action of magnetic charges with the help of the concept of “lines of force.”15 This is a legitimate practice inasmuch as force is a property of scalar motion, as Larson explains. Referring to Figure 1a, we see that the magnetic lines of force are in tension in the longitudinal direction, and have a positive pressure in the transverse direction; that is, they tend to contract along their length, and to diverge out in the perpendicular direction.
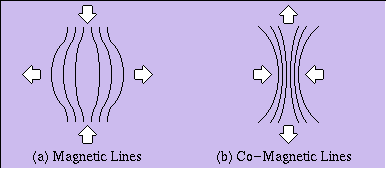
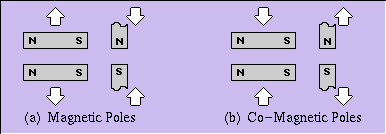
Because the direction, in the context of the conventional reference system, reverses whenever a motion crosses a unit boundary (even though it continues in the same natural direction), the behavior of the magnetic lines of force in the equivalent space would be as shown in Figure 1b. They tend to expand in the longitudinal direction, and to concentrate in the transverse direction. In other words, like poles attract and unlike poles repel (see Figure 2a and 2b). In view of this reversal of the apparent directions, we will give this phenomenon a new name, and call it co-magnetism.
4.2 Domain Configurations of Magnetism and Co-magnetism
We will now highlight some significant patterns of the field line arrangements that are derived from the nature of magnetism and co-magnetism respectively, as these will have a bearing on the explanation of the magnetic field structure of the sun.
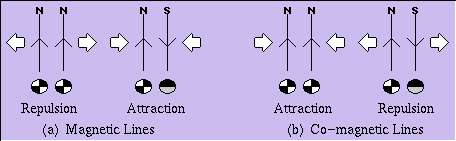
Consider two pairs of parallel field lines, with the field directions as shown in Figure 3a. Let us refer to the field line coming out of the plane of the paper and represented by a plus sign as the “north line” and the one antiparallel to it, and represented by the minus sign, as the “south line.” As can be seen from the figure, in the case of normal magnetism, two parallel north (or south) lines repel each other, while north and south lines attract each other. If we now imagine a process that generates equal numbers of south and north lines, all of which remain parallel to each other, but are free to move in the lateral direction, the least energy configuration would be one in which there are no large-scale magnetic domains, as shown in Figure 4a.
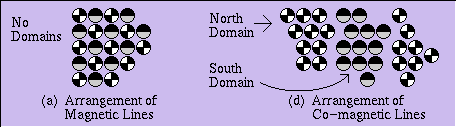
Turning now to the case of co-magnetism, we find that two north (or south) lines attract each other, while north and south lines repel each other (Figure 3b). Suppose that in a co-magnetic process, equal numbers of north and south lines are generated in such a way that they are constrained to remain parallel to each other, but are free to migrate laterally. If initially the south and north lines are randomly distributed in space, lines of the same type tend to aggregate and form separate magnetic domains. At the same time, domains of opposite polarity tend to repel each other and move apart (see Figure 4b). If the total volume in which these domains exist is restricted, then the eventual result of the gradual merging of the domains of the same polarity would be the complete bifurcation into two domains of opposite polarity.
5 Summary of Part I
Summing up some important conclusions reached regarding the structure of matter at very high temperatures:
-
Matter in the ultra high temperature range manifests as slender, unidirectional, expanding threads that keep forming and dissolving. These have been named Thredules.
-
Thermal motion beyond unit level produces magnetic fields.
-
Inasmuch as these fields are in equivalent space, the magnetic effects in the three-dimensional reference system are the opposite of the normal magnetic effects. This phenomenon is named Co-magnetism.
Part II: The Solar Interior and the Sunspots
In Part 1 of this paper, we have endeavored to develop some important properties of matter at very high temperatures—those that prevail in the stellar interiors. Utilizing the principles developed there, we will now attempt to deduce the internal structure of the sun. For ease of reference, the section numbers, the figure numbers, and the reference numbers are all continued from Part 1.
6 Morphology of the Solar Core
We have noted that the energy generation in the stars is by the thermal destruction process, and that preliminary calculations5 establish that the thermal destructive limits of the elements are in the ultra high temperature range. So the central region of the sun is composed of matter at the intermediate and the ultra high temperatures. The matter in the ultra high temperature core manifests as an ensemble of thredules, which we have seen to be thin, straight, continuous filaments (Section 3.3). We now note that both these thredules, and the embedded co-magnetic field lines that run along the length of these filaments are expanding in the longitudinal direction (Section 4.1).
The directions of the thredules have to be randomly oriented in the three-dimensional space of the reference system when no factor providing for a preferred direction exists. But since the sun is rotating, the axis of rotation does provide such a preferential direction. As such, the great majority of the thredules form in a direction parallel to the axis of rotation.
Once the general direction of the thredules is fixed, we can deduce that, by the operation of probability, half of these will have north magnetic flux lines threading through their length, while the remaining half will have south magnetic lines (the qualifications “north” and “south” being merely chosen for the sake of convenience of reference, and do not mean to point to any external magnetic field).
6.1 Formation of the Two Sheaves of Thredules
For reasons explained in Section 4.2, the south and north thredules segregate into two principal domains of opposite magnetic polarity. Given no other factors, therefore, one would expect the ultra high temperature core to assume a configuration in which two co-axial, cylindrical sheaves of north and south thredules respectively occur.
Since we have seen (Section 4.2) that two parallel co-magnetic lines of the same magnetic field direction attract each other, the minimum energy configuration for either of the sheaves mentioned in the preceding paragraph would be one in which all the thredules are mutually parallel. However, at the interface between the two sheaves we find thredules of opposite magnetic field direction occurring adjacent to each other. Since parallel co-magnetic lines of opposite field directions tend to repel (Section 4.2), we see that the above arrangement of the two sheaves does not yield the least energy configuration for the interface.
Therefore, the above configuration would give way to another in which the interficial energy is also reduced. This could be readily achieved by tilting the adjacent thredules of the two sheaves in opposite directions, while, at the same time, keeping the adjacent thredules of any one sheaf mutually parallel. This would render the cylindrical shape of each sheaf into a hyperboloid. The final configuration of the two sheaves of thredules at the beginning of a solar cycle will be that of two co-axial hyperboloids, as shown in Figure 5. For the sake of clarity, only a few of the thredules of each sheaf are shown in the figure.
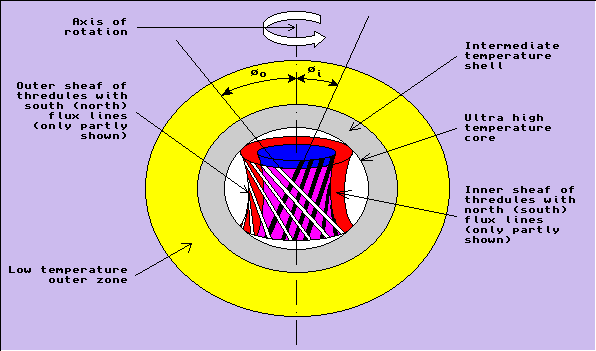
(schematic diagram only—not to scale)
Let us denote the angles of inclination of the thredules of the inner and outer sheaves with respect to the direction of the axis of rotation of the sun by θi and θo respectively. Remembering that the thredules tend to maximize their length (Section 3.3) and so do the co-magnetic lines (Section 4.1), one can easily compute that the optimal values of θi and θo would be ±45°. (More involved calculations point out that θi would be around 50°, and θo around -40°.) In Figure 5, the inner thredules are shown inclined such that θi = +45°, while the outer thredules with θo = -45°.
6.2 Effect of the Progress of the Solar Cycle
The thredule structure does not extend beyond the ultra high temperature core. The co-magnetic field lines running along the thredules, however, jut out into the outer layers. When they emerge out into the low temperature regions where the magnetic effects are in the space of the reference system, instead of in equivalent space, lines of opposite field directions join in U-loops and start exerting attractive force. This tends to effectively anchor the tips of the thredules of opposite field directions. We might imagine the circular edges of the inner and the outer hyperboloidal sheaves respectively to be jointed at each end.
Now while retaining these anchorages at the ends, if the inclination of all thredules is altered by some angle, say θ, then θi becomes θ + 45° and θ0 becomes θ - 45°. This means that the inner thredules would be pointing to lower latitudes and the outer ones to higher latitudes. The effect on the shape of the two hyperboloids would be such that the inner one gets more separated from the outer. Consequently, the repulsive interficial energy decreases further. Therefore, this is what happens with the progress of the solar cycle, as shown in Figure 6: the inner thredules go on tilting toward lower and lower latitudes, and their average length increases, while the outer thredules of opposite magnetic polarity go on tilting toward higher and higher latitudes, and their average length decreases.
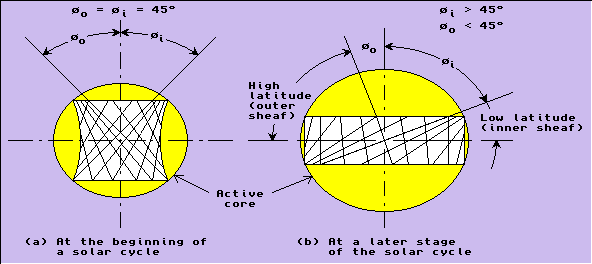
7 Birth of the Sunspots
The sun’s atmosphere consists of three distinct layers; the lowest is the photosphere with an estimated depth of 200-400 km, followed by increasingly rarefied and transparent layers of the chromosphere and the corona. The bulk of the energy is emitted by the photosphere as continuum radiation. The opacity of the photosphere increases very rapidly with depth, producing the illusion of a sharply defined outline of the sun. The effective temperature of the photosphere, on the basis of blackbody assumption, is estimated to be 5780° K.
7.1 Observational Description
Sakurai gives a graphic account of how sunspots form:
“At first, a localized magnetic field appears… In general, sunspots start out as pores, which are small regions much darker than the surrounding photosphere… the magnetic field strength increases significantly… and a full-fledged sunspot group develops. The sunspots are concentrated in the preceding… and the following… ends of the group…
“The magnetic field has different polarity in the spots belonging to the preceding and following ends… It is well-established that most sunspot groups appear as bipolar.
“… a fully developed sunspot consists of the central dark umbra, through which most of the magnetic flux is channeled, and the less dark penumbra.
“The magnetic field strength has a maximum value near the center of the spot, or where the spot is darkest, i.e., the core of the umbra. The strength of the magnetic field is about 1,000-5,000 gauss for well-developed sunspots… The fully developed sunspot may exist for days, weeks, or months…”16
7.2 Explanation of the Origin
We will see that the explanation of the structure of the solar core we have delineated earlier logically leads to the explanation of the origin and properties of the sunspots and the associated phenomena. In the beginning of the previous section, we have noted that the thredules (as well as the co-magnetic lines embedded in them), tend to expand in the longitudinal direction. As they do so and penetrate into the lower temperature outer regions, they give up heat to the surrounding material and eventually drop into the intermediate temperature region and cease to exist as thredules. However, at times due to the local variations in the energy generation process, thredules with large enough energy shoot outwards with sufficient violence as to reach the top of the atmosphere before getting dissolved.
As this ultra high temperature matter breaks through the photosphere, it makes its appearance as a sunspot of low temperature (for reasons explained in Section 3.3) and is seen as a sunspot. Thus, the sunspots are hotter and not cooler than the surrounding photosphere. The characteristic of the co-magnetic field lines to bunch together in the transverse direction naturally produces a field intensity sharply increasing toward the center or core of the spot umbra, which is the hottest (though ostensibly the coolest) portion.
Between the two sheaves of thredules oppositely inclined to the rotation axis (Figure 5), the inner one is naturally at a higher temperature. Moreover, as the solar cycle advances, the thredules in the inner sheaf become longer, while those in the outer become shorter (Figure 6). Consequently, the great majority of the sunspots arise out of the shooting of the more energetic inner thredules. In fact, the magnetic polarity of the precursors of an emerging bipolar spot group is that of these inner thredules. Thredules of opposite magnetic polarity, being induced outwards by the action of the precursors, emerge to form the spots of opposite polarity of the sunspot group. As we will see presently, these latter always appear on the “following” end of the group, and a little while later than the precursors.
As those of the thredules belonging to the inner sheaf, and which will be emerging at the photospheric level as the leader spots travel through the matter of the intermediate temperature shell surrounding the core, that matter in the immediate vicinity of these passing thredules gets heated up. Some of this matter in the line of travel rises to the ultra high temperature level and transforms into the thredule state (see Figure 7). The co-magnetic lines in these induced thredules will, of course, be of opposite polarity. These induced thredules, therefore, appear as the spots of the opposite polarity when they emerge at the photospheric level. The general finding that the preceding spot appears first, develops first, and disappears last, is exactly what is to be expected from our above theoretical account if we remember that the induced thredules are less energetic, as well as time-lagged, compared to the inducing thredules.
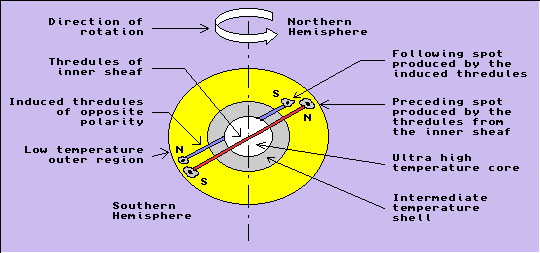
The reason why the induced spots always form behind, with reference to the direction of rotation of the solar surface may not, however, be readily understood. We have already noted in Section 3.3 that the motion at the ultra high speed pertains to a scalar dimension altogether different from the scalar dimension that is coincident with the conventional reference system.11 Even though such motion does not produce direct effects in the reference system, being itself a motion in space it always acts to oppose the motion represented in the reference system. Inasmuch as the motion in the dimension of the reference system did produce changes of position in that system, the overcoming of that motion (by the ultra high speed motion in the second scalar dimension) reverses those changes of position. The position of the induced thredule, thus, would be located at a little angular distance backwards compared to the position of the inducing thredule relative to the direction of rotation of the sun. This produces the separation between the preceding and the following members of a spot group.
8 Sunspot Properties
8.1 Characteristics of the Spot Groups
Figure 7 illustrates one of Hale’s polarity laws of sunspot groups: namely, that the polarity of the preceding (following) spots in each hemisphere is opposite. We have just now explained its origin.
Currently, the formation of spot groups is being attributed to the buoying up of toroidal magnetic flux tubes supposed to be subsisting below the photosphere. If this were to be true, all spot groups have to be bipolar. The occurrence of unipolar and those classified as complex groups cannot be accounted for.
Large-scale, low intensity magnetic regions of the photosphere within which sunspots rarely appear are referred to as the bipolar magnetic regions (BMR), and the unipolar magnetic regions (UMR). Like the bipolar sunspot groups, the BM regions also are found to obey Hale’s polarity laws. It is not difficult to see that these regions arise as the thredules and the embedded co-magnetic lines shoot outwards, but the thredules give up heat and completely dissolve prior to reaching the visible layers of the photosphere, whereas the co-magnetic lines emerge out. Since they are no longer in equivalent space when they so emerge, these lines no longer bunch together, but tend to diverge and their intensity falls to a low value. This is the origin of the magnetic regions. Once again, in the conventional theory it is difficult to account for existence of the UM regions.
“The belts where sunspots most frequently appear migrate from high latitudes around 35° - 40° at the start of the new solar activity cycle, to the low latitude region around 5° - 10° at the end of the solar activity cycle. This migration of the sunspot producing areas occurs at almost the same time in both the northern and southern hemispheres.”17 We have already arrived exactly at this finding by theoretical deductions toward the end of Section 6 above. Bray and Loughheed, who have done extensive work on sunspot studies, comment, “The cause of the latitude drift is very obscure.”18
Solar prominences are arch-like structures, which appear as dark filaments against the solar disk, but appear luminous at the limb. There are two types of prominences: one type appears in the region of 45° latitude where sunspot groups are born and migrates with them toward the equator, as shown in Figure 8.19 The other type is not associated with sunspots, and appears around 45° latitude and tends to migrate polewards, reaching the pole toward the maximum of the solar activity cycle. Both types of prominences are known to form along the borders between magnetic regions of opposite polarity. The magnetic polarity distribution around the polar prominences is opposite to that around the spot prominences, as indicated in Figure 8. Sakurai states, “… as yet we do not know the cause of this relationship… This subject is not yet fully understood in spite of extensive efforts to discover the cause of the formation of solar magnetic fields, both sunspot and ’general’.”20
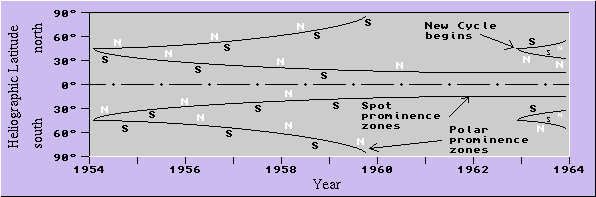
(adopted from Reference 19)
But our theoretical derivation correctly predicts this state of affairs: in Section 6 we have shown that the thredules of the outer sheaf assume higher latitude positions with the advance of the solar cycle. These thredules are shorter and less energetic and succeed in producing only the bipolar magnetic regions in the photosphere, and not the sunspots. It is evident that the polar prominences are associated with these regions. Since the inner and the outer thredules are of opposite polarity, the preceding and following members of the BMR associated with spot prominences (arising from the inner thredules) are of opposite polarity compared to the corresponding members of the BMR associated with polar prominences (arising from the outer thredules). The migration of the two classes of BMRs, one poleward, and the other toward the equator, is similarly explained (see the end of Section 7.2).
Before leaving the subject of prominences, we should mention that scientists find it hard to explain why the gaseous material arching out in space sustains the filamental shape, when there is nothing to prevent its lateral expansion. Sakurai remarks, “Even now we do not have a definite explanation of how the cool gas constituting the prominences is supported by the magnetic lines of force of the sunspots, because this gas may easily diffuse out without resistance from the magnetic lines of force.”21 But we have already seen why the matter in the very high temperature range retains the thread-like structure and how expansion in the context of such temperatures is observed as contraction.
We will now move on to the explanation of another observational fact—a fact which the conventional theories find most difficult to explain—namely, the reversal of the polarity scheme of the bipolar spot groups in both the hemispheres with each new cycle of solar activity. This is expressed as another of Hale’s polarity laws: “The entire system of polarities remains unchanged during any one 11-year cycle of sunspot activity, but reverses with the beginning of the next cycle…
“The reversal… begins with the appearance of spots of the new cycle in high latitudes before the spots of the old cycle have completely disappeared.”22 (See Figure 8.)
The beginning of the next cycle of the energy generation process takes place at the center of the sun as the temperature there once again reaches the thermal destructive level of the element present there. This creates a fresh pair of inner and outer sheaves of thredules lying inside the pair of sheaves belonging to the old cycle. The thredules of either sheaf of the new cycle also will be inclined at nearly 45° on either side of the axis, respectively. In view of the fact that the co-magnetic lines of like polarity have an affinity to each other, two things happen. Firstly, the thredules of the outer sheaf of the new cycle will form inclined to the axis on the same side in which the thredules of the inner sheaf of the previous cycle happened to be inclined. Secondly, the magnetic polarities of the thredules of these two sheaves will be identical. Since the polarity of the thredules of the inner sheaf is opposite to that of the thredules of the outer sheaf, we have the final result that the polarity of the thredules of the inner sheaf (and hence of the preceding spots) of the new cycle is opposite to the polarity of the thredules of the inner sheaf (and that of the preceding spots) of the old cycle.
8.2 The Sunspot Penumbrae
Soon after the appearance of a sunspot, the surrounding material of the photosphere in its immediate neighborhood starts becoming darker and at some subsequent stage, thin filaments directed more or less radially outwards from the spot umbra form. These annular regions around the umbrae are referred to as the penumbrae. The lengths of these radial filaments are known to vary according to the spot size and complexity. The radiation intensity in the penumbra gradually decreases inwards from the photosphere to the penumbra-umbra border, where it falls very steeply. The filaments end abruptly such that this border is sharply outlined.
Bray and Loughhead state: “It must be admitted that neither the mode of origin of the penumbra nor the role it plays in the sunspot phenomenon as a whole is yet properly understood.”23 However, we can readily see that the penumbra must comprise of the photospheric material heated up to the intermediate temperature by the thredules that form the spot umbra. Both its filamental configuration, and sharply demarcated interface with the umbra suggestive of the phase change that occurs on crossing the boundary between the ultra high speed region and the intermediate speed region, clearly point to this.
Observations of sunspots near the solar limb show a marked asymmetry in the penumbral width (the Wilson effect) that seemed to suggest that the sunspots are saucer-like depressions in the photosphere. But recent observations with improved resolution never revealed such depressions when seen right up to the limb. The Wilson effect results if the umbra is much more transparent, rather than the penumbra, as compared to the photospheric material. This, of course, is what is to be expected. Opacity is a result of the absorption of radiation by the processes of photoionization and photoexcitation. With increasing temperature, more and more atoms are completely ionized, and the scope for the above absorption processes decreases. Therefore the matter in the penumbra is more transparent than the low temperature photospheric matter and that in the umbra more transparent than both of these.
8.3 The Evershed Effect
Radially outward motions in the sunspot penumbrae (parallel to the photospheric surface), named as the “Evershed velocities” (after their discoverer) are known to exist. No vertical or tangential velocities were ever observed in the penumbrae. The radial velocity—radial to the spot—increases from about 1.0 km/sec at the boundary between umbra and penumbra, reaches a maximum of about 2.0 km/sec near the center of the penumbra and comes to zero at the outer edge of the penumbra. It is also known that the Evershed velocity increases with the depth.
According to Bray and Loughhead:
“…The simplest interpretation of the Evershed effect is that it consists of a laminar flow of matter outwards from the umbra along the filaments…
“One piece of evidence against the hypothesis is the observed variation of the Evershed velocity with height: this would seem to be of sufficient magnitude to prevent the occurrence of a purely laminar flow… the shearing effect of the vertical velocity gradient would quickly lead to the disintegration of the filaments. Yet individual filaments are observed to persist…
“No trustworthy mechanism for the origin of the driving force of the Evershed flow has yet been proposed. It is rather interesting to note that at the photospheric level the direction of the motion is opposed to the pressure gradient, the pressure in the umbra being less than that in the photosphere.”24
All the above description of the Evershed effect exactly fits our theoretical conclusion that the penumbral matter is in the intermediate temperature range. The commencement of the radial velocity with a finite value (instead of a zero value) at the boundary of the umbra, the sustained laminar-like flow, despite the existence of a steep velocity gradient in the vertical direction, the apparent motion against the pressure gradient, all of these point to the same thing, namely, that the motions in the penumbra pertain to the region of equivalent space.
In Section 3.2.4 we have shown that thermal motion beyond the unit level tends to contract a material aggregate. Therefore the decrease in the intermediate temperature with the increase in the penumbral radius involves a re-expansion that extends all along the radius. Although this manifests as a flow in the penumbral filaments, in reality, its true nature is altogether different.
We shall let Larson explain it:
“At this time we will take a look at another of the observable effects of motion in time… its effect in distorting the scale of the spatial reference system.
“… in the physical universe we are able to use the spatial reference system only on the basis of an assumption that the rate of change of time remains constant… the scale of spatial co-ordinate system is related to the rate of change of time… At speeds in excess of unity, space is the entity that progresses at the fixed normal rate, and time is variable. Consequently, the excess speed above unity distorts the spatial co-ordinate system.”25
Thus at higher intermediate temperatures there will be a greater scale distortion (in the manner of contraction) and vice versa.
The Evershed flow is not a genuine change of position of the particles of matter in the space of the reference system: it is, rather, the effect of the occurrence of a scale gradient accompanying the temperature gradient in the intermediate region.
8.4 Evidence Against the Apparent Low Temperature of the Spots
8.4.1 Intensity Measurements
The radiation intensity of the sunspots is measured at several frequency ranges. The current practice of treating this radiation as conforming to the continuum spectrum of the blackbody radiation has lead to conflicting results.
Bray and Loughhead remark, “As a direct consequence of the umbra’s low temperature, its spectral class is later than that of the photosphere—dKo as compared to dGo-2 for the photosphere.” Then on making a comparison with the observed intensity values they conclude: “It follows that the spectral class of the umbra is decidedly earlier than the temperature derived from intensity measurements made in the continuous spectrum would lead one to expect. The origin of this discrepancy is unknown.”26 This must be so, as long as the true status of this radiation is not recognized.
Quoting again from them: “…numerous weak [spectral] bands due to unidentified compounds have so far been seen only in spots, and… unidentified bands in the sunspot spectrum are more numerous than those now accounted for.”27
8.4.2 Sunspot Effects on the Surrounding Granulation
The entire surface of the photosphere appears covered with uniformly bright cells, called the granules, separated by the darker intergranular material. These granules are believed to be convection cells. Observations show that there is an increase in intensity at the Violet and UV wavelengths giving rise to the appearance of bright, ring-like regions around the spots.
Bray and Loughhead report that it is “found that the intensity of the bright ring is greatest immediately outside the penumbra and decreases slowly outwards… the bright rings are unusually intense around spots showing large Evershed velocities.”
“No satisfactory explanation of the presence of the bright rings in the photosphere around spots… has yet been given.”28 Rightly so. But the moment we realize that the spots are hotter and not cooler than the photosphere, then enhanced brightness can be attributed to the energy transfer from the spot.
Moreover, from heat transfer studies, it is known that an increased heat transfer rate is correlated with smaller size of the convective cells. We see from Bray et al that “the size distribution of the solar granulation is extremely uniform over the solar surface…
“…Several authors have observed a reduction in the granule diameter or mean spacing in the close neighborhood of sunspots…, which so far has received no theoretical attention.”29 In addition, these areas of reduced granule size adjacent to the spots are found to coincide with the regions of enhanced brightness mentioned above.30
8.5 Polarization of the Radiation
Polarization measurements on the integrated radiation from the sunspots indicates that it is partially plane polarized. This, of course, is what is to be expected (see the end of Section 3.1).
9 Radiation Associated with Sunspots
We have already discussed some aspects of the magnetic fields, the prominences, and the granulation in association with the spots.
In addition to the continuum and line emission, different other patterns of radiation emission are observed in conjunction with sunspot groups. Non-thermal radio emission in the metric frequency range is often found above spot groups and is known as the Type I continuum storm. Such sunspot groups with Type I emission are also found responsible for the generation of solar flares (sudden, local increases in the surface brightness of the sun).
Emission of micro-waves, soft thermal X-rays, high energy particles (of MeV-BeV range), hard non-thermal X-rays, gamma rays, and non-thermal burst emissions at radio frequencies are all known to occur in the several phases of the solar flares. Some of the radiation is seen to be strongly polarized. The scientists admit that as yet no satisfactory and consistent explanation of the complex nature of these radiation phenomena is available.
Larson discusses at length the processes that generate non-thermal X-rays and radio waves.2 He explains how stable isotopes become radioactive and emit radiation at radio wavelengths when they are transported from the low temperature region to the intermediate temperature region. In a similar manner, he shows that when matter which has attained isotopic stability in the intermediate temperature region is transported to the low temperature region, it again becomes radioactive and emits X-rays and gamma rays.31 As such, it is not difficult to account for the origin of the variety of the observed radiations in association with the sunspots, once the presence of the ultra high and the intermediate speed matter in and around them is recognized.
10 Epilog
We have shown that reasoning from the principles embodied in the Reciprocal System it is possible to explore the internal structure of the sun. The theoretical understanding so obtained is in consonance with the observations of sunspot and relevant phenomena.
The main thesis derived is that sunspots are produced by the surfacing of the ultra high temperature matter in the solar core in the form of “thredules” to the photospheric level.
It must be mentioned that the theoretical account of the solar interior herein reported is a simplified one that is meant to serve as the basis for further, more detailed, work.
1 Larson, Dewey B., Nothing But Motion (North Pacific Publishers, Portland, OR, 1979)
2 Larson, Dewey B., Universe of Motion (North Pacific Publishers, Portland, OR, 1984)
3 ibid., page 41.
4 ibid., pages 61-62.
5 Nehru, K.V.K., “Intrinsic Variables, Supernovae and the Thermal Limit,” Reciprocity XVII (1), Spring, 1988, page 20.
6 Larson, Dewey B., Universe of Motion, op cit., pages 70-73.
7 Larson, Dewey B., Nothing But Motion, op.cit., page 155.
8 Larson, Dewey B., Universe of Motion, op cit., page 215.
9 ibid., page 224.
10 ibid., page 215-216.
11 ibid., page 213.
12 ibid., page 214.
13 ibid., page 223.
14 ibid., page 364.
15 Larson, Dewey B., The Neglected Facts of Science (North Pacific Publishers, Portland, OR, 1982), pages 9-12.
16 Sakurai, Kunitomo, Physics of Solar Cosmic Rays (University of Tokyo Press, Japan, 1974), page 53.
17 ibid., page 55.
18 Bray, R.J., and Loughhead, R.E., Sunspots (Chapman & Hall, New York, 1964), page 244.
19 Sakurai, Kunitomo, op. cit., page 63.
20 ibid., page 64.
21 ibid., page 94.
22 Bray, R.J., and Loughhead, R.E., op. cit., pages 242-243.
23 ibid., page 276.
24 ibid., pages 151, 154.
25 Larson, Dewey B., Nothing But Motion, op. cit., page 107.
26 Bray, R. J., and Loughhead, R.E., op. cit., page 132.
27 ibid., page 140.
28 ibid., pages 66-67.
29 Bray, R.J., Loughhead, R.E., and Durrant, C.J., The Solar Granulation (Dover Publishers, 1979), pages 41, 86.
30 ibid., page 88.
31 Larson, D. B., Universe of Motion, op. cit., pp. 248, 249.
