RS2-109: Dimensional Thinking

“An alien intelligence is going to be more advanced. And that means efficiency functioning on multiple levels and in multiple dimensions.”

—S. R Hadden (from the film, Contact)

Human perception is based primarily on 1- and 2-dimensional thinking. For example, all locations in space can be connected by a 1-dimensional line, regardless of how many twists and turns it takes to get from start to end.

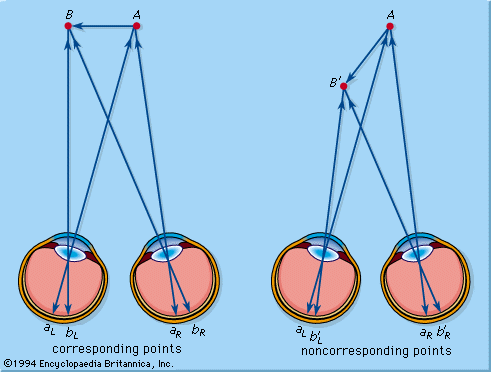Our vision works like a 2-dimensional projection screen with a lens focusing an image on the surface of the retina. With two eyes, the mind can give the illusion of three dimensions by focusing on a distant point to create a triangular relationship and estimate the distance to that point. But we don’t actually “see” in three dimensions… we internally recreate a 3-dimensional geometry from 1 and 2-dimensional information. If we had senses that perceived three dimensions, one would be able to see the back of an object as clearly as the front.

This modality of thought has carried over into everything we do with our senses, including the inductive theories created by observation. Dewey Larson created his “reciprocal system” through induction, observing that the atoms of the Periodic Table could be accurate expressed by three magnitudes, rather than a 1-dimensional atomic number—if those magnitudes were the inverse of spatial magnitudes. From this pattern, he hypothesized that this “inverse magnitude” must be time, as mechanically described by the concept of speed—the inverse relation of space to time. But that also inferred that time, like space, had three dimensions and both space and time were related to each other as aspects of motion. From this he developed his theory of a universe of motion, now known as the Reciprocal System of physical theory.

From this inductive theory, Larson created two postulates to define his conceptual basis, then proceeded to deduce the structure of the physical universe¹ from those postulates to see how close it matched the original observation.

Larson, however, was still caught in the paradigm of 1-dimensional, linear thinking. This is evidenced by the fact that he could have linear motion without anything moving, but could not have angular motion without something to rotate. In his case, the photon provided the “stick” to spin into the concept of the rotational base—one dimension spinning to make two. Yet, he also postulates that the Universe is 3-dimensional in nature.

In his paper, “The Law of Conservation of Direction,”² Prof. KVK Nehru states, “Rotation is precluded only if space is one-dimensional. Just as soon as it is established that the stationary spatial reference system is three-dimensional, rotation becomes a possibility” and introduces the concept of rotation being primary, meaning that the angular velocity behind rotation is just as likely as the translational velocity of Larson’s direction reversal—rotation without anything to rotate.

By making rotation primary (a constant, angular velocity), the photon could now be represented by a 2-dimensional quantity, the complex number, with the “real” aspect being the translational speed of the outward progression and the “imaginary” aspect acting as a rotational operator to specify the angular velocity (frequency) of the rotation.

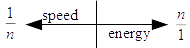Nehru’s concept was actually buried in Larson’s own research, concerning the idea of units of motion that represented three possible “speed ranges” of any specific motion. The basis of this is Larson’s speed-energy relationship, where any motion could exist as either a unit of speed (1/n) or energy (n/1), as a simple matter of arrangement, not requiring any addition or loss of energy to change between the two.

Speed was Larson’s first unit of motion (1-x speed range) and energy was the second (2-x range). Energy, having its “direction reversal” in time (n/1, the 1 being +1 -1 +1 = 1) had to be expressed in equivalent space, which is a 2-dimensional form of space representing the effect time has upon space. Speed, in space, was a linear translation (v), but because equivalent space was a 2^nd power function, speed in equivalent space is orbital (v²), making equivalent space Larson’s version of the “imaginary” number. Nehru’s concept of “rotation as primary” is just Larson’s motion in equivalent space.

But this is still 1-or-2 dimensional thinking, in a 3-dimensional universe. Larson’s work is basically done on a number line, where all the values are real. Nehru extended Larson’s work into the complex plane, giving two dimensions to motion. What happens if we take “thinking” up to three dimensions?

The first thing we run into is an old problem from the 1800s that puzzled researchers into imaginary quantities: how to increase the rotational dimensions of the “points on a plane” of complex numbers into “points on a sphere,” where it becomes impossible to calculate the quotient of the coordinates of two points in space. This was resolved by William Hamilton in 1843 with his concept of the quaternion: a 4-dimensional quantity that had a real, scalar value coupled to a rotational triplet—three rotations, not two, made it work. Continued investigation found that there were only four dimensional structures that were solvable, 1, 2, 4 and 8 dimensions, known today as division algebra.

Larson did attempt to take motion into a 3^rd unit through the use of his ultra-high (3-x) speed range, incrementing the 2^nd unit of motion, energy, into the first unit (speed) of a 2^nd dimension of motion and reversing its scalar direction, though there is no conceptual reason why that would happen.

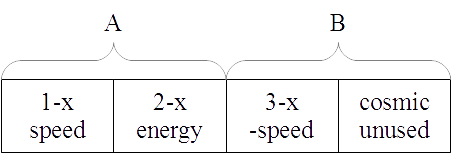
Larson uses the ultra-high speed range primarily in the discussion of astronomical objects, where such motion can be observed. As a general concept it works, but when applied to specific equations, fails for the same reasons Hamilton ran into. But Hamilton’s solution works just as well in the Reciprocal System.

Larson does omit “unit speed” from his concept of “units of motion,” which should not have been omitted because he does assign unit speed values to many motions. However, if we apply Hamilton’s quaternion structure to Larson’s units of motion we need four units instead of three, but the resulting structure does explain a lot:

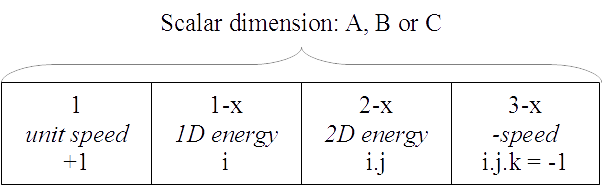
Remembering Hamilton’s bridge scrawling, i² = j² = k² = i.j.k = -1, examine the structure. First off, we eliminate the 2^nd scalar dimension of motion as unnecessary, assigning all four “units of motion” to a single, scalar dimension. This has the added bonus of making all three scalar dimensions homogeneous; with Larson’s approach, the 2^nd dimension (B) is split in half, different from the first (A) and third (C, not shown).

• The first unit is outward speed—a real magnitude that is the progression of the natural reference system, underlying all motion.

• The second unit (1-x) is 1-dimensional (1.i) and imaginary, expressing energy as an electric rotation.

• The third unit (2-x) is 2-dimensional (1.i.j) and imaginary, expressing energy as a magnetic rotation.

• The last unit (3-x) is back to a 1-dimensional, real magnitude of opposite direction to the first unit, an inward speed (1.i.j.k = -1).

As a quaternion (rather than a 2D triplet), motion can express itself in four symmetric forms, two of them being linear (outward and inward speed) and two rotational (1D electric and 2D magnetic energy). And now we have a clear concept of why 3-x motion is inward speed (aka gravity)—it is the direct consequence of 3D rotation, in a 3-dimensional Universe of motion.

This quaternion structure also provides a more accurate definition of the photon. In quaternion math, 2D rotation of i.j is equivalent to 1D rotation of k; i.j = k. If i.j is paired with a -k rotation, you end up with (k)(-k) = +1, two counter-rotating systems (Nehru’s birotating photon) producing a cosine wave that has a net, outward, unit speed in space: a wave traveling at the speed of light.

Nehru’s birotation has two, 1-dimensional electric rotations that reduce to a cosine wave in space.³ The quaternion model has a 2-dimensional, magnetic rotation coupled to a 1-dimensional, electric rotation, making the quaternion photon electromagnetic radiation, solely from its structure. As such, it would also have various orientations, resulting in the various transverse photon modes (TE, TM, TEM), which are not a consequence of Larson’s or Nehru’s models.

Thinking in three dimensions has produced an improved model of Larson’s units of motion and of Nehru’s birotating photon. But division algebra supports 1, 2, 4 or 8 dimensions, so what happens if we start to think in multiple dimensions like the aliens in Hadden’s comment, starting this paper? We can still hard-code a three-dimensional universe, but by applying a variable number of units of motion per dimension, a mathematical system evolves that accurately represents all of the known motions in the Reciprocal System, which is unique in that it includes life as a “natural consequence” of motion:⁴

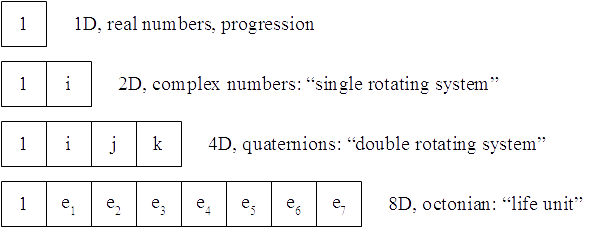
The 1-dimensional, real numbers represent the outward expansion of the universe at unit speed, the speed of light. This “unit of motion,” though used in the Reciprocal System frequently, was never defined as a unit of motion.

The 2-dimensional, complex numbers represent a single, electric rotating system, electrons and positrons.

The 4-dimensional quaternion represents Larson’s “double rotating system,” that forms the basis of particles and atoms, and electromagnetic in nature. Quaternions model the photon and neutrinos.

The 8-dimensional octonian represents an interlinked structure of double rotating systems that are the mathematical model of a screw, vortex or helix. These structures are basic to life units, such as the α-helix of the protein. The octonian can be considered the “particle” version of a living cell.

Each of these dimensional algebras can exist in either a single or dual form, such as a pair of quaternions that are joined with the epsilon function (ε), that keeps them separate, yet interlocked. This duality creates the remaining rotational structures of the Reciprocal System, as they work cooperatively:

Dual complex forms the birotation necessary for the vibrational motion of charge.

Dual quaternions are the “two double-rotating systems” that form atomic structure, starting with the proton.

Dual octonians express the life unit, the biological cell, linking the material and cosmic structures together, combining the linear motion of space with the rotational motion of time.

By using a combination of division algebra dimensions to express Larson’s “units of motion” concept, all the rotational structures (both material and cosmic) can be mathematically represented with real numbers, complex quantities, quaternions and octonians. This solves many of the problems with trying to use fixed dimensions and units, creating a very concise mathematical progression of complexification from the unit speed motion of the progression of the natural reference system, all the way up to the biological cell of the life unit.

---