CHAPTER 6
The General Picture
Translation of the mathematical properties of reciprocals into the physical terms applicable to scalar motion, a reciprocal relation between space and time magnitudes, in the preceding chapter revealed that there necessarily exists an inverse sector of the universe in which the scalar motions of our familiar material sector are duplicated in inverse form with space and time interchanged. The phenomena of one dimension of the inverse type of motion can therefore be represented in a three-dimensional temporal reference system corresponding to the three-dimensional spatial reference system in which spatial motion is customarily represented. Our next undertaking will be to extend our consideration of the properties of reciprocals to an investigation of the intermediate regions between the regions represented in the two types of three-dimensional reference systems.
For this purpose we will need to consider the manner in which the primary scalar motions are combined. As noted earlier, the photons of radiation have no capability of independent motion, and are carried outward at unit speed by the progression of the natural reference system, as shown in (1), Diagram A. All physical objects are moving outward in the same manner, but those objects that are subject to gravitation are coincidentally moving inward in opposition to the outward progression. The information developed from the investigation of scalar motion does not indicate the exact nature of the gravitating objects, which we identify from observation as atoms and sub-atomic particles, but for present purposes this knowledge is not essential. When the gravitational speed of such an object is unity, and equal to the speed of progression of the natural reference system, the net speed relative to the fixed spatial reference system is zero, as indicated in (2). In (3) we see the situation at the maximum gravitational speed of two units. Here the net speed has reached -1, which, by reason of the discrete unit limitation, is the maximum in the negative direction.
| Motion | In | Out | Net | |||
|---|---|---|---|---|---|---|
| (1) | Photon | Progression | | | ——> | +1 | |
| (2) | At grav. limit | Progression | | | ——> | ||
| Gravitation | <—— | | | ||||
| (3) | At maximum gravitation | Progression | | | ——> | -1 | |
| Gravitation | <—— | | | —— | |||
| (4) | At zero net speed | Progression | | | ——> | ||
| Gravitation | <—— | | | —— | |||
| Translation | | | ——> | ||||
| (5) | At unit net speed | Progression | | | ——> | +1 | |
| Gravitation | <—— | | | —— | |||
| Translation | —— | | | ——> | |||
An object moving with speed combination (2) or (3) can acquire a translational motion ín the outward scalar direction. This is the type of motion with which we will be concerned in the remainder of this volume. One unit of the outward translational motion added to combination (3) brings the net speed relative to the fixed reference system, combination (4), to zero. Addition of one more translational unit, as in combination (5), reaches the maximum speed, +l, in the positive scalar direction. The maximum range of the equivalent translational speed in any one scalar dimension is thus two units.
As indicated in Diagram A, the independent translational motions with which we are now concerned are additions to the two basic scalar motions, the inward motion of gravitation and the outward progression of the natural reference system. The net speed after a given translational addition therefore depends on the relative strength of the two original components, as well as on the size of the addition. That relative strength is a function of the distance. The dependence of the gravitational effect on distance is well known. What has not heretofore been recognized is that there is an opposing motion (the outward progression of the natural reference system) that predominates at great distances, resulting ín a net outward motion.
The outward motion (recession) of the distant galaxies is currently attributed to a different cause, the hypothetical Big Bang, but this kind of an ad hoc assumption is no longer necessary. Clarification of the properties of scalar motion has made it evident that this outward motion is something in which all physical objects participate. The outward travel of the photons of radiation, for instance, is due to exactly the same cause. This is a significant point because no tenable explanation of this phenomenon has heretofore been available, and the conclusion derived deductively from the new facts discovered in the scalar motion investigation fills a vacuum in the existing structure of physical theory. Einstein is generally credited with having supplied an explanation, but actually he conceded that he was baffled. In one of his books he points out that this is an extremely difficult problem, and he concludes that
Our only way out… seems to be to take for granted the fact that space has the physical property of transmitting electromagnetic waves, and not to bother too much about the meaning of this statement.72
Objects, such as the galaxies, that are subject to gravitation, attain a full unit of net speed only where gravitation has been attenuated to negligible levels by extreme distances. The net speed at the shorter distances is the resultant of the speeds of the two opposing motions. As the distance decreases from the extreme values, the net outward motion likewise decreases, and at some point, the gravitational limit, we will call it, the two motions reach equality, and the net speed is zero. Inside this limit there is a net inward motion, with a speed that increases as the effective distance decreases. Independent translational motions, if present, modify the resultant of the two basic motions.
Aggregates of matter smaller than the galaxies are under the gravitational control of larger units, and do not exhibit the same direct connection between distance and net speed that characterizes the galaxies. The same two opposing basic motions are, however, effective regardless of the size of the aggregate, and the equilibrium to which they lead can be recognized in a number of astronomical phenomena. The globular star clusters are a good example. These clusters are huge aggregates of stars, up to a million or more, in a nearly spherical structure, that are observed in the outlying regions of the larger galaxies. No viable explanation has heretofore been found for the continued existence of such a cluster. Only one force is known to be applicable, that of gravitation, and an equilibrium cannot be established without the presence of some equally powerful antagonist. Rotational forces often play the antagonist role in astronomy, but there is little rotation in these clusters. A dynamic equilibrium, as in a gas, has also been suggested, but a gas sphere is not a stable structure unless it is confined. On the basis of what is now known, the cluster should either dissipate relatively quickly, or collapse into one central mass. It does neither. Since there is no explanation available, the whole issue has been shelved by the astronomers for the time being.
The outward progression of the natural reference system now supplies the missing ingredient. Each star is outside the gravitational limits of its neighbors, and therefore has a net outward motion away from them. Coincidentally, however, all stars are subject to the gravitational effect of the cluster as a whole. In a relatively small cluster the inward gravitational motion toward the center is not sufficient to hold the cluster together, but as the size of the cluster increases, the gravitational effect on the outer stars increases correspondingly. In a very large aggregate, such as a globular cluster, the net motion of the outer stars is inward, acting against the outward motion of the inner stars, and confining all stars to equilibrium positions.
Once the nature of the cluster equilibrium is understood, it is evident that the same considerations apply to the galaxies, although the rotational forces in these more complex structures modify the results. The existence of the scalar motion equilibrium accounts for some otherwise unexplained properties of the galactic structure. For instance, the minimum observed separation between stars in the outer regions of the Galaxy (aside from that in double or multiple star systems) is more than two light years, an immense distance that is inexplicable without some specific obstacle to a closer approach. The existence of an equilibrium distance similar to that in the globular clusters now provides the explanation. The fact that the stars occupy equilibrium positions rather than moving freely in interstellar space also gives the galactic structure the characteristics of a viscous liquid, which explains a number of effects that have heretofore been difficult to understand, such as the confinement of quantities of high energy matter in the central regions of certain galaxies.
The units of translational motion that are applied to produce the speeds in the higher ranges are outward scalar units superimposed on the motion equilibria that exist at speeds below unity, as shown in combination (5), Diagram A. The two-unit maximum range in one dimension involves one unit of speed, s/t, extending from zero speed to unit speed, and one unit of inverse speed, t/s, extending from unit speed to zero inverse speed. At this point it will be convenient to identify inverse speed as energy. This identification plays no part in the development of thought in the remainder of this work, and anyone who is inclined to question it can simply read “inverse speed” wherever “energy” appears in the subsequent discussion. The reason for using the “energy” designation is to keep the terminology of this work uniform with that of the previous theoretical publications. As has been emphasized repeatedly in the foregoing pages, this work is purely factual, and independent of any theory, but the conclusions reached herein are identical, as far as they go, with the corresponding results of the theoretical investigation. Inasmuch as these factual conclusions conflict with currently accepted physical theory in many respects, they constitute strong evidence in favor of the validity of the theory of a universe of motion. Many readers of this volume will no doubt wish to examine the published descriptions of that theory, and to facilitate such an examination it is desirable to use the same terminology that was employed in the theoretical publications.
For the benefit of those who may feel that the use of the term “energy” in this significance is definitely ruled out by a conflict with the kinetic energy equation, in which the energy varies as the square of the velocity, rather than being inversely related, it should be noted that the energy does not vary with v2 alone, but with mv2. As we found earlier, mass is a measure of a distributed scalar motion. Thus mv2 is a compound motion, a motion of a motion. Energy, in this context, is velocity of a mass. Since we are not undertaking to develop a theory of motion in this work, we are not in a position to establish the equivalence of this compound motion and the inverse of simple scalar motion, but the status of mv2 as a compound motion means that there is nothing in present-day physical theory (which does not recognize this kind of motion) to indicate that the presence of the v2 term in the energy equation is inconsistent with the identification of inverse speed as energy. This is all that it is necessary to know for present purposes.
Unit speed and unit energy are equivalent, as the space-time ratio is 1/1 in both cases, and the natural direction is the same; that is, both are directed toward unity, the datum level of scalar motion. But they are oppositely directed when either zero speed or zero energy is taken as the reference level. Zero speed and zero energy in one dimension are separated by the equivalent of two full units of speed (or energy) as indicated in this diagram:
DIAGRAM B
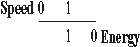
In the foregoing paragraphs we have been dealing with full units. In actual practice, however, most speeds are somewhere between the unit values. Since fractional units do not exist, these speeds are possible only because of the reciprocal relation between speed and energy, which makes an energy of n/1 equivalent to a speed of 1/n. While a simple speed of less than one unit is impossible, a speed in the range below unity can be produced by addition of units of energy to a unit of speed. For reasons that require a theoretical explanation, and are therefore beyond the scope of this factual presentation, the quantity 1/n is modified by the conditions under which it exists in the spatial reference system, and appears in a different mathematical form, usually 1/n2 (actually [ l / n]2).
In this connection, it may be well to point out that this work does not undertake to supply the reasons why things are as they are—that is the task of fundamental theory. Where the reasons are necessary consequences of known facts, they are, of course, included with the other factual material, but otherwise the results of observation are accepted as they are found. In the case now being considered, the second power expression, 1/n2, is well established empirically, appearing in numerous observationally verified relations.
As noted earlier, unit speed and unit energy are oppositely directed when either zero speed or zero energy is taken as the reference level. The scalar direction of the equivalent speed 1/n2 produced by the addition of energy is therefore opposite to that of the actual speed, and the net speed in the region below the unit level, after such an addition, is 1-1/n2. Motion at this speed often appears in combination with a motion 1-1/m2 that has the opposite vectorial direction. The net result is then 1/n2-1/m2, an expression that will be recognized as the Rydberg relation that defines the spectral frequencies of atomic hydrogen—the possible speeds of the hydrogen atom.
The net effective speed 1-1/n2 increases as the applied energy n is increased, but inasmuch as the limiting value of this quantity is unity, it is not possible to exceed unit speed (the speed of light) by this inverse process of adding energy. To this extent, we can agree with Einstein’s conclusion. However, his assertion that higher speeds are impossible is incorrect, as there is nothing to prevent the direct addition of one or two full units of speed in the other scalar dimensions. As we saw in Chapter 4, this means that there are three speed ranges, identified in that chapter as 1-x, 2-x, and 3-x.
Because of the existence of three speed ranges with different space and time relationships, it will be convenient to have a specific terminology to distinguish between these ranges. In the subsequent discussion we will use the terms low speed and high speed in their usual significance, applying them only to the region of three-dimensional space, the region in which the speeds are 1-x. The region in which the speeds are 2-x—that is, above unity, but below two units—will be called the intermediate region, and the corresponding speeds will be designated as intermediate speeds. Speeds in the 3-x range will be called ultra high speeds.
Inasmuch as the three scalar dimensions are independent, the two-unit range between zero speed and zero energy applies to each of these three dimensions individually. Thus the total separation between zero speed and zero energy on the full three-dimensional basis is six units of speed (or energy). The midpoint that divides the material (space) sector from the cosmic (time) sector is three units. In practice, however, neither net speed nor net energy exceeds the two-unit level by any significant margin, because of the gravitational effects. This is illustrated in Diagram C, which shows the relations between the speeds and energies of the two sectors.
DIAGRAM C
SCALAR UNITS OF SPEED AND ENERGY
| 1. 2. |
Material sector | at s=0 at s>1 |
0 1 |
1 2 |
2 3 |
3 |
|||||||
| 3. | Natural system | 1 | 2 | 3 | (2) | (1) | (0) | ||||||
| 4. 5. |
Cosmic sector |
at t>1 at t=0 |
(3) |
(3) (2) |
(2) (1) |
(1) |
|||||||
The middle line in this diagram (number 3) shows the total speeds and energies (in parentheses), with 3 units of either speed or energy as the midpoint. Where gravitation is absent, as it is (on the individual mass unit basis) at any distance above that corresponding to unit speed, or any inverse distance above that corresponding to unit energy (lines 2 and 4), the effective speeds are the same as in line 3. The upper (1) and lower (5) lines show the net values with gravitation included.
The significance of this diagram is that it demonstrates that the effective maximum net speed (or energy) is not three units, the midpoint between zero speed and zero energy, but two units. We know from observation that at the normal (low) speeds of the material sector the spatial density of matter is great enough to subject all aggregates to gravitational effects. In view of the reciprocal relation, we can deduce that the same is true of the density in time in the cosmic sector. Motion in space does not change the density in time, and vice versa. It follows that when the net spatial speed (translational less gravitational) reaches 2 units (line 2), gravitation in time becomes effective, and the motion is at the (3) level on the energy basis (line 5).
Summarizing the foregoing discussion, we may say that the physical universe is much more extensive than has hitherto been realized. The region that can be accurately represented in a spatial frame of reference is far from being the whole of the universe, as conventional science assumes that it is. There is another equally extensive, and equally stable, region that is not capable of representation in any spatial reference system, but can be correctly represented in a three-dimensional temporal reference system, and there is a large, relatively unstable, transition zone between the two regions of stability. The phenomena of this transition zone cannot be represented accurately in either the spatial or temporal reference systems.
Furthermore, there is still another region at each end of the speed-energy range that is defined, not by a unit speed boundary, but by a unit space or time boundary. In large-scale phenomena, motion in time is encountered only at high speeds. But since this inversion from motion in space to motion in time is purely a result of the reciprocal relation between space and time, a similar inversion also occurs wherever the magnitude of the space that is involved in a motion falls below the unit level. Here motion in space is not possible because less than unit space does not exist, but the equivalent of a motion in space can be produced by means of a motion in time, since an energy of n/1 is equivalent to a speed of 1/n. This region within one unit of space, the time region, we may call it, because all change that takes place within it is in time, is paralleled by a similar space region at the other end of the speed-energy range. Here the equivalent of a motion in time is produced inside a unit of time by means of a motion in space.
As we have just seen, in connection with the combination of speeds and energies to produce net speeds below unity, the mathematical expression of the speed equivalent of an energy magnitude may take a form that differs from the expression of the corresponding speed. This difference in the mathematics, together with the substitution of energy for speed, accounts for the difficulty, mentioned in Chapter 3, that conventional physical theory is having in defining the phenomena of the realm of the very small in “real” terms.
With the addition of these two small-scale regions to those described above, the speed regions of the universe can be represented as in Diagram D.
| Speed | 0 | 1 | 2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| time | : | 3d | : | scalar | : | 3d | : | space | ||
| only | : | space | : | zone | : | time | : | only | ||
| 2 | 1 | 0 | Energy | |||||||
The extent to which our view of the physical universe has been expanded by the identification of the properties of scalar motion can be seen from the fact that the one section of this diagram marked “3d (three-dimensional) space” is the only part of the whole that has been recognized by conventional science. Of course, this is the only region that is readily accessible to human observation, and the great majority of the physical phenomena that come to the attention of human observers are phenomena of this three-dimensional spatial region. But the difficulties that physical science is currently encountering are not primarily concerned with these familiar phenomena; they arise mainly from attempts that are being made to deal with the universe as a whole on the basis of the assumption that nothing exists outside the region of three-dimensional space.
Our results show that the principal problems now confronting physics and astronomy stem from the fact that observation and experiment have penetrated into these regions that are beyond the scope of the three-dimensional space to which present-day theorists are limiting their vision. The phenomena and entities of the hitherto unrecognized regions of the physical universe interact with those of the region of three-dimensional space only at widely scattered locations. We therefore encounter them one by one at apparently unrelated points. For a full appreciation of their significance it needs to be realized that all of these seemingly isolated items are constituent elements of a vast physical system that is mainly beyond the reach of our physical facilities.
The concept of phenomena that either cannot be represented accurately, or cannot be represented at all, within a three-dimensional spatial system of reference, will no doubt be unacceptable to many individuals who are firmly committed to the long-standing belief that the region defined by such a system is the whole of physical existence. But this is simply another case of anthropomorphism, not essentially different from the once general conviction that the earth is the center of the universe. Nature is under no obligation to conform to the manner in which the human race perceives physical events, and in order to enable continued progress toward better understanding of natural processes it has been necessary time and time again to transcend the limitations that men have tried to impose on physical phenomena. Extension of physical theory into regions beyond representation in the conventional spatial reference systems is a drastic change, to be sure, but the fact that such an extension turns out to be required should not surprise anyone who is familiar with the history of science.
As indicated in Diagram C, when the distance exceeds 1.00, the gravitational limit, and gravitation is consequently eliminated, the limiting value of 2-x is at the sector boundary. Any further addition to the speed results in entry into the cosmic sector. It is possible, however, for an object to acquire a translational speed of 3-x and still remain in the material sector until the opposing gravitational motion is reduced to the point where the net total speed of the object reaches two units.
Thus far we have been considering the successive units of speed purely as magnitudes. On this basis, they are all equivalent. As we saw in Diagram B, however, the second unit in each scalar dimension is a unit of energy, rather than a unit of speed. lt is equivalent to a unit of speed in magnitude, but in relation to zero speed it is inverse, and opposite in direction. Motion in this speed range is in time. The effect of the reversal at the unit level is to divide the two sectors of the universe into regions in which the relation between the natural and arbitrary spatial reference systems changes at each regional boundary. Since the natural system is the one to which the universe actually conforms, any process that, in fact, continues without change across a regional (unit) boundary reverses in the context of the arbitrary fixed spatial reference system. Each region thus has its own special characteristics, when viewed in the context of the spatial reference system.
The observed characteristics of motion in the intermediate region, for instance, are quite different from those of motion in the speed range below unity. However, the differences are introduced by the connection to the reference system; they are not inherent in the motions. So far as the scalar motion itself is concerned, these are two one-unit positive magnitudes of the same nature. The fact that one of these motions takes place in space, and the other in time, is a result of their relation to unity, the natural datum, or zero level.
A speed 1-x is less than unity, and it causes a change of position in space, without effect on position in time (relative to the natural datum). A speed of 2-x, in the intermediate range, is greater than unity, and it causes a change of position in time. Further addition of speed, bringing the motion into the 3-x range, the ultra high speed range, puts it over the one-dimensional limit of two units, and into the spatial unit of a second dimension. Such a motion is outward in space in the second dimension, while it continues outward in time in e first dimension. As noted earlier, coincident motion in both space and time is impossible. But we have seen that a motion with energy n/1 in time is equivalent to a motion with speed 1/n in space. As long as the gravitational effect is strong enough to keep the net total speed below the sector limit of two units, the motion as a whole continues on the spatial basis. The motion in time that takes place in the 2-x and 3-x speed ranges while the net speed is below two units is therefore a motion in equivalent space.
The upper speed ranges are duplicated on the energy side of the neutral level. Corresponding to the intermediate speed range is an intermediate energy range, with energy 2-x, where x is the fractional energy equivalent of n units of speed. In this energy range, the motion as a whole continues on the time basis as long as the net total energy remains below the two-unit level. The motion in space that takes place in this 2-x energy range is therefore a motion in equivalent time.
Similarly, a motion component in the 3-x energy range, which involves motion in time in one dimension and motion in space in a second dimension, continues as a motion in equivalent time as long as the net total energy remains below the level at which gravitation begins acting in space.
Like the phenomena of the low energy range, the region of three-dimensional time, the events taking place in the two upper energy ranges are outside our observational limits, and we know them only by analogy with the corresponding events on the space side of the neutral level. However, events in the upper speed ranges produce some effects that are observable. An examination of these effects will be our next undertaking, and will be the subject of Chapter 7.
Some general comments about the contents of this present chapter are in order. First, it may seem that the large number and broad scope of the conclusions that have been reached are out of proportion to the base from which it is asserted that they are derived, inasmuch as the stated objective was to derive them from the mathematical properties of reciprocals. It should be remembered, however, that the point brought out in Chapter 5 was that application of these mathematical properties to any particular set of physical circumstances would define the physical properties. Notwithstanding the essential simplicity of scalar motion, it is subject to a wide variety of such physical circumstances, by reason of (1) the existence of positive and negative scalar magnitudes, (2) the limitation to discrete units, and (3) the three-dimensionality of the physical universe. The number of permutations and combinations of these factors is enormous.
The second point that warrants some consideration is the logical status of the conclusions that have been reached with respect to the phenomena of the regions intermediate between the region represented in the conventional spatial reference system and the corresponding inverse region. It has been found empirically that certain things (using the term in a broad sense to include both entities and phenomena) do exist in the physical universe. These, particularly the ones that have not heretofore been recognized, constitute the basis for the development of thought in this present volume. In the course of this development, we find that certain things must exist as a consequence of the things that we observe do exist. For example, we have seen that the observed existence of a fundamental force requires the existence of a fundamental motion. Further results of the development of the consequences of the established facts in both of these categories then reveal that certain other things can exist. Ordinarily, this would not imply that they do exist, but there is one influential school of thought in science that takes the stand that in nature anything that can exist (or happen. There is no clear distinction, from the natural standpoint, between what exists and what happens) does exist. K. W. Ford expresses this point of view:
One of the elementary rules of nature is that, in the absence of a law prohibiting an event or phenomenon, it is bound to occur with some degree of probability. To put it simply and crudely: anything that can happen does happen.73
In any event, whether we can assert that some physical objects actually do attain speeds in the intermediate and ultra high ranges, or whether the most that we can legitimately say is that they can attain such speeds, what we need to do in order to bring speeds of this magnitude into the factual picture that we are developing in this work is to identify physical objects whose properties coincide with the properties of objects moving at speeds in excess of that of light. lt is evident that such objects, if they exist, are astronomical. This introduces some difficulties into the identification process. The amount of observational information about astronomical phenomena is, in many cases, severely limited. “What is a quasar? No one knows,”74 says Gerrit Verschuur (1977). Why is the matter of the universe aggregated into galaxies? “This is the most glaring and basic unsolved problem in astronomy,”75 according to M. J. Rees. To make matters worse, an unknown, but probably substantial, proportion of what is currently regarded as knowledge is actually misinformation. “Much of what is known today must be regarded as tentative and all parts of the field have to be viewed with healthy skepticism.”76 (Martin Harwit)
In order to compensate for the scarcity of reliable information about the nature and properties of the individual astronomical entities, the identifications based on comparison with this information will be supplemented by identification of entire classes of objects or phenomena. For example, a whole class of compact astronomical objects will be identified as material aggregates whose high density is due to the same cause: component speeds in the intermediate (2-x) range. Similarly, a process of aggregation, observed only at isolated points, will be identified in its entirety. It could be said that the next chapter, in which most of these identifications will be made, is, in total, a comparison of the properties of the intermediate region, as derived by deduction from factual premises, with the corresponding region of the astronomical universe. In other words, it is an identification of the intermediate region as a whole. Chapters 5 and 6 were devoted entirely to the development of the relevant facts. Now Chapter 7 will be devoted entirely to the process of identification.
In the course of this identification process, however, we will advance our understanding of the intermediate speed region a step farther than was possible in the preceding discussion. The physical entities that we will identify as moving at speeds greater than unity are active participants in large-scale physical activity. Thus, in examining and identifying these entities we will also be deriving a general picture of the large-scale action of the universe.
