CHAPTER III
Simple Linear Motion
The basic premise of this work, as explained in Chapter II, is that the physical universe is a universe of motion. The task of constructing a comprehensive theory of this universe, from which we can derive an explanation of the quasars and the pulsars, therefore reduces to nothing more than determining just what kinds of motion are possible, and what changes from one to another can take place under what circumstances. As a base from which to start, we have expressed the general characteristics of the motion in the form of two fundamental postulates, and from this point on we will simply be developing the necessary consequences of those postulates.
In beginning this development, we note first that motion, as defined for the purposes of these postulates, is inherently a progression. This is consistent with the usual textbook definition of motion which uses the expression “continuous change,” or its equivalent, but we are utilizing the term “progression” to emphasize the fact that although motion exists only in discrete units, it is a continuous process, not a series of jumps. A unit of motion is a specific section of the progression, and there is progression even within that unit, simply because this is the nature of the entity; the unit is a unit of progression.
Since time is merely one aspect of motion, it, too, progresses. In dealing with this progression it will be convenient to introduce the concept of location. Any designated portion of the time progression, the size of which will vary with the circumstances, is a location in time. In common usage such a location is identified by reference to an arbitrary datum and is expressed in a form such as 1492 A.D. Now let us anticipate the subsequent development to the extent of recognizing that this development will reveal the existence in the physical universe of certain specific physical entities which, for present purposes, we will call “objects.” If such an object existed at time location 1492 A.D. and had no mechanism whereby it could change its position relative to time, we recognize that 100 years later the object would no longer be found at 1492 A.D., but would exist at a different time location, 1592 A.D. This, then, is one concept of time location. But if we look at the situation from another standpoint, it is obvious that any object which has no independent motion must remain at the same location. Thus we have here another concept of location, which we will call absolute location. As a general principle we may say that any object which has no independent motion with respect to time remains at the same absolute location in time and is carried forward by the time progression.
The situation is similar to that of a boat on a river. We may specify the position of such a boat in either of two ways. First, we may locate it with reference to some point or points on the river bank. This we will call its coordinate location, as where accuracy is desired a system of coordinates will normally be utilized. Alternatively, we may specify the location of the boat with respect to the stream, the absolute location, as we have just defined it. If the boat is without power it remains permanently in the same absolute location, the same position in the stream, and in that case its change of coordinate location is determined entirely by the rate of stream flow, not by any property of the boat itself. If the boat is in motion under its own power, the change of coordinate location is the net resultant of the stream flow and the movement of the boat relative to the stream.
By reason of the reciprocal relation between space and time all that has been said about time in the preceding discussion is equally applicable to space. Space, like time, is an aspect of motion, and like time, it progresses. Here, too, an object which has no independent motion with respect to space remains at the same absolute space location, and is carried along by the space progression. As it happens, most of the familiar objects of our everyday experience do have independent motions with respect to space, and for this reason the existence of the space progression has not heretofore been recognized, but there is ample evidence of its existence, as we will see shortly.
Another consequence of the reciprocal relation between space and time is that each individual unit of space is equivalent to an individual unit of time. In primitive or undifferentiated motion, therefore, the progression of space and the progression of time take place coincidentally. For some purposes it will be convenient to regard this basic motion as a joint progression, a progression of space-time, motion in its most general form. This progression takes place uniformly, because each unit of space (or time) is equivalent to any unit of time (or space) , and consequently all units of space (or time) are alike. It takes place at unit speed, one unit of space per unit of time, and outward, because increasing space accompanies increasing time. Any object which has no independent motion with respect to either space or time remains in the same absolute space-time location.
Those who have difficulty in conceiving of motion that is not motion of something may find it helpful to regard the progression of space-time as motion of the absolute reference system, the natural reference system to which the physical universe conforms, with respect to the stationary coordinate reference system that we recognize in our daily life. This is analogous ta the motion of the stream, the reference system for floating objects, with respect to the river bank, the reference system for a stationary observer.
Another useful analogy compares this expanding space-time system, the absolute reference system, to an expanding balloon. An expanding three-dimensional object, something on the order of an expanding solid ball, would provide a still closer analogy, but the expanding balloon is a very familiar object, and there should be no difficulty in extrapolating whatever conclusions we reach on this basis from two to three dimensions. Corresponding to the physical objects without independent motion that we have been considering, we may visualize spots painted on the surface of the balloon. The distance between these spots is continually increasing as the balloon expands, but this is not due to any actual motion of the spots; they are fixed to the surface and they cannot move. The increase in separation is a property of the system, the expanding balloon system in which the spots are located.
If, in addition to the spots, there exist some objects on the surface of the balloon which can move independently, flies perhaps, the true measure of that independent motion will not be the observed increase in separation between these objects and adjacent spots, but the amount by which that observed increase is more or less than that which would have taken place by reason of the expansion alone if the objects had remained fixed to the balloon surface in the manner of the painted spots. Ordinarily we look upon the balloon as being located in three-dimensional space, and we view the motion of objects on the balloon surface in the context of a three-dimensional reference system. But it is obvious that any fixed reference system gives us a completely distorted picture of what is going on. It attributes motion to objects such as the painted spots which cannot and do not move, and it gives us a totally unrealistic account of the motion of any objects that do move. For a correct assessment of the situation we must use a moving reference system. Outward motion at the rate of expansion constitutes the datum—the balloon zero, we might call it from which we must measure in order to arrive at the true motion of objects on the balloon surface.
The physical situation is similar. We live in a universe which is continually expanding because of the equivalence of the unit of space and the unit of time. Here, too, as on the surface of an expanding balloon, the use of a fixed reference system gives us a completely distorted picture of what is happening. It attributes motion at high velocities to some objects that are no more capable of independent motion than the painted spots on the balloon; it portrays other objects as approximately at rest when they are, in fact, moving at high velocities, and so on. As in the case of the expanding balloon, we can get the true picture only by the use of a moving reference system. We must take the expansion as our datum and measure our quantities from there.
This does not mean that motion with respect to a fixed system of reference is of no consequence to us. On the contrary, such motion is usually our primary concern in the everyday affairs of life. But trying to account for the existence and magnitude of relative motions of this kind on the basis of some hypothetical properties of the physical objects concerned is in the same category as trying to account for the movement of a powerless boat relative to a point on the bank by means of some property of the boat itself. In both cases the situation can be clarified only by recognizing that the physical object involved is located in a moving system—in one case the flowing river, in the other the expanding universe.
The significant point here is that the basic undifferentiated motion outward at unit speed, one unit of space per unit of time, is the physical equivalent of nothing at all; it is the datum from which all physical activities extend, the reference system to which all such activities, or phenomena, can be related. In order that there may be physical phenomena there must be some deviation from this basic uniformity, some displacement, as we will call it, of the one-to-one space-time ratio either in the direction of more space or of more time, and the amount of this displacement determines the magnitude of the phenomenon. The basic physical quantities are not measured from the mathematical zero, but from this unit space-time ratio.
This concept of a “displacement” of the space-time ratio seems to present some difficulty to a number of those who have undertaken to follow the development of theory, but all that is necessary here is to keep in mind that when we use the term “displacement” we are talking about speed. More than one individual has asked at this point, “If you mean speed, why don’t you say speed?” The reason is that displacement is not merely speed; it is speed measured in an unfamiliar way from an unfamiliar reference point.
As the term is used herein, space or time displacement is measured from unity; it is the deviation from the one-to-one ratio of space to time that constitutes unit speed. Thus it is the deviation from what we may call the physical zero—or perhaps more accurately, the neutral point—rather than from the mathematical zero that constitutes the datum from which speed is ordinarily measured. Furthermore, the study of basic physical phenomena is largely a matter of determining the effects of successive additions of units of space or time to existing motions, and it will therefore be convenient to work with quantities that are measured in terms of such units. For example, a change from the neutral level that would be reported in terms of speed as a reduction of ½ unit followed by a reduction of 1/6 unit, would be reported in terms of displacement as an addition of one time displacement unit followed by another addition of the same kind: a statement that is much more significant from a theoretical standpoint.
The question that naturally arises at this point is, How can these displacements of the space-time ratio exist, when each unit of space is always equivalent to a unit of time? Inasmuch as the progression is scalar, the only variation that can take place is in the scalar direction: outward (positive) or inward (negative). If both space and time are progressing outward, the unit ratio is maintained. The same is true if they are both progressing inward, or if one is progressing outward and the other inward. But there is one further possibility. One of the components may alternate scalar directions, so that the negative progression of one unit of this component cancels the positive progression of the preceding unit. A series of such reversals thus results in the formation of a multiple unit of motion in which n units of space (or time) are associated with only one unit of time (or space). The sense of the reciprocal postulate is that in these multiple units of motion the n units of one component are equivalent to 1/n units of the other.
Of course, this does not necessarily demonstrate that such reversals do take place; it merely indicates that they can take place. As indicated at the beginning of this chapter, however, the task of constructing a theory of a universe of motion is essentially a matter of determining what variations of motion can exist and what consequences follow. The theoretical universe is therefore a description of the possible rather than the actual. The final tie-in with reality is provided by showing that what can exist in the theoretical universe coincides with what does exist in the actual physical universe.
While the existence of the displacements is thus explained, the postulates do not provide any means whereby such displacements may be created or destroyed. Consequently, the existing displacements have the character of postulates; they are given features of the universe rather than items developing out of the operation of physical processes. The present total of such displacements must therefore remain constant (unless it can be altered by some agency outside the physical universe. Whether or not such an agency exists is, of course, beyond the scope of this work.) Here is the conservation law in its most general form.
If the change in scalar direction takes place in space, so that n units of time become associated with one unit of space in a velocity ln, the result is a change of location in space. A location which normally would have advanced n units of space during n units of time now advances only one unit. We will describe such a change of location as motion in space. There might be some merit in applying the “space” designation to the displacement which is responsible for this motion, especially since it is the space component that deviates from the normal rate of progression. However, the net effect of a displacement of this character is to increase the number of time units taking part in the particular phenomenon from one to n; that is, n/1 units have, in effect, been added to the time component of the motion while the space component remains at unity. It will therefore be convenient to call this a time displacement, so that when we add time displacement we are adding time, and when we add space displacement we are adding space.
Inasmuch as the limiting value of the quantity 1/n, the spatial speed, is 1/1, it is evident that motion in space cannot take place at a net speed greater than unity. However, this does not mean that there are no net speeds greater than unity; it merely means that such speeds are not spatial speeds. They are temporal speeds, and they result in change of position in time rather than change of position in space. All this follows automatically from the reciprocal relation between space and time.
It also follows from this same relation that whatever is true with respect to the spatial speed is equally true, when the appropriate changes in language have been made, of the inverse (temporal) speed n/1. We can say, then, that a space displacement causes a motion in time, which results in a change in time location. Such a motion cannot have a net speed of less than unity, as the limiting value of the quantity n/1 is 1/1.
These simple motions which are now under consideration are inherently scalar. Whatever spatial or temporal directions may be attributed to them are determined by the reference system that is employed, not by any property of the motions, and assignment of direction by selection of a reference system does not alter their scalar characteristics. Unfortunately, it is not generally realized that such a thing as inherently scalar motion exists. In fact, the usual physics textbook ignores scalar motion altogether and lists motion (velocity) , together with its primary derivatives—acceleration, etc: as typical examples of vector quantities. The scalar aspects of this vectorial motion are given due consideration. For example, speed is distinguished from velocity. But the existence of motion that has no inherent direction is not mentioned.
However, inherently scalar motion does exist, even in the everyday world. If we examine the motions of the spots on the surface of the balloon that we have been using for purposes of analogy, we will find that they are quite different from ordinary vectorial motions. For instance, if there are three physical objects A, B, and C, in a straight line, and we give the center object B a motion in the direction away from A, it moves toward C. But if we consider three spots X, Y, and Z, located in a similar straight line on the surface of an expanding balloon, we will find that while the motion of the center spot Y carries it away from X, just as the motion of B carried it away from A, spot Y does not move toward Z in the same manner as B moves toward C; it actually moves away from Z. Furthermore, it moves away from all spots in all directions; that is, it is moving outward in all directions. This means, of course, that it has no direction of its own, the motion is inherently scalar. Whatever direction may be attributed to it in the context of a particular reference system is a property of that system, not of the motion of Y.
Such phenomena as the motion of spots on the surface of an expanding balloon are of little consequence in human life, and the failure of previous investigators to give serious consideration to the scalar motion phenomenon is therefore quite understandable. At the very beginning of our development of the consequences of our fundamental postulates, however, we arrive at the conclusion that the basic motions of the universe are inherently scalar—the normal space-time progression, for instance, is simply outward, without any further qualification—and the status of scalar motion is thereby changed from a matter of little significance to a fundamental factor of major importance. The subsequent development in this volume can be clearly understood only if it is recognized that both the space-time progression and gravitation (which will be discussed in the next chapter) are inherently scalar.
While a scalar quantity, by definition, has no direction, in the spatial or temporal sense of that term, and has magnitude only, that magnitude may be either positive or negative, as we have already noted. To complete the definition of such a quantity we must specify this scalar direction, as well as the numerical magnitude. In the context of a three-dimensional reference system this quantity, if it is a motion, also acquires a spatial or temporal direction.
This raises another question with respect to terminology. In the first publication in this series, the term “direction” was used in three different applications, including the two just specified. This is technically in order, as the word “direction” has a wide range of meanings in general usage, extending even to nonphysical items, such as the direction of our thinking. But some readers have pointed out that this practice tends to cause a certain amount of confusion, and they have suggested that three different terms be utilized. As it happens, however, the various senses in which the term has been employed are not entirely independent, and for this reason it has seemed advisable to continue the use of “direction” in all three applications, but to add some further identification to distinguish between them. We will therefore speak of vectorial direction, scalar direction (inward or outward) , and space-time direction (toward more space or toward more time). Where the term “direction” is used without any qualification it is to be understood as meaning vectorial direction, the direction with reference to a three-dimensional coordinate system.
On this basis, any specific unit of the normal space progression has a scalar direction: outward. In the context of a spatial reference system it also has a vectorial direction in three-dimensional space, which we may call AB. If the scalar direction reverses at the end of this unit, in the manner previously discussed, and the next unit of the progression is inward, the vectorial direction also reverses; that is, the direction of the motion with respect to the spatial reference system is now BA. The situation here may be compared to the motion of an automobile, which not only has a vectorial direction such as north or south, but also has a scalar direction, in that it may run either forward (positive) or backward (negative) independently of the vectorial direction in which it is traveling. If the car is on a very narrow road, analogous to the one-dimensional path of the space-time oscillation, and it runs forward in moving north, then if it reverses its scalar direction—that is, runs backward—it moves south.
Reversal of the scalar direction of the motion, as well as the direction relative to a fixed reference system, causes each unit of the alternating progression to cancel the entire effect of the preceding unit, and the net change of location during a two-unit cycle is zero. The directional reversal thus results in an oscillation at a location in three-dimensional space that is stationary in the dimension of the oscillation.
Here we have the first physical abject, the first entity that we encounter in our theoretical development that can be distinguished from the general background. But this is not yet an object with an independent motion. Aside from the oscillation, which causes no net change in location, this object has no capability of motion with respect to either space or time, and it must therefore remain permanently in the same absolute space-time location. As brought out in the preceding discussion, this means that it moves outward relative to a fixed reference system at unit speed. Since the oscillation is the progression in the original dimension, the outward motion takes place in a dimension perpendicular to the oscillation.
The specific nature of the reversals in the oscillating unit is not self-evident, but we can clarify it by noting that a reversal, or any other change in the motion, is equivalent to superimposing a second motion on the original. This second motion necessarily has both a space aspect and a time aspect, hence it involves at least one unit of each. A reversal, or other change, of motion in space (or time) therefore cannot be accomplished in less than one unit of time (or space). Each reversal therefore begins at the midpoint of one unit and is completed at the midpoint of the unit following. The combination of an oscillating motion in one dimension with an outward progression in a perpendicular dimension thus takes the form of a sine curve in three-dimensional space (or time).
It is essential to recognize that there is no general reference system to which all spatial quantities can be related. (Nor is there a general reference system for all temporal quantities. In this and similar discussions referring specifically to space, it should be understood that the same considerations also apply to time by reason of the reciprocal relation.) The concept of space as a setting or background in which physical objects exist, as used in the theoretical systems of Newton and Einstein, must be discarded when we accept the idea that we live in a universe of motion, but we can set up a three-dimensional reference system that is essentially equivalent to Newton’s “absolute space” for translational motion only. If we start at a location in space, as previously defined, and observe the space-time progression from this point, we will find that it can be represented as an expanding sphere with the initial point at the center. The absolute location of the initial point will be somewhere on the surface of a sphere of radius x after x units of time have elapsed. We may then insert three perpendicular axes into this sphere, thus defining a three-dimensional coordinate system to which we can refer locations in space.
A similar reference system can be defined from any other location as a center, but if the sphere centered at location A continues to expand it will ultimately reach the sphere centered at location B, and will thus establish a definite relation between the two, so that locations in both systems can be expressed in terms of either. Any one such system is therefore a universal system of reference. However, it is only a reference system—nothing more—and it is a reference system for translational motion only. The significance of this, in the present connection, is that the space which enters into the oscillation just described cannot be represented in the translational reference system. The oscillating unit is an entity that exists in a location defined by that reference system, but the motion of which it is constituted is totally independent of the translational space.
Later in the discussion we will encounter a striking illustration of this independence of the spatial aspects of different kinds of motion. There are certain combinations of motion that are essentially nothing more than mobile units of space, and we will find that they are able to move through matter, which in turn occupies a location in translational space. To those accustomed to thinking of space as a three-dimensional background for physical events, such an idea seems totally absurd, but this is only because the development of thought on the basis of a universe of matter has equated “space” with the space aspect of translational motion. Once it is realized that the conventional “space” is merely the reference system for translational motion, and that the space aspect of other types of motion is independent of the translational reference system, this difficulty disappears.
It may be mentioned in passing that the spatial aspects of the vibrations and rotations that we encounter in our ordinary experience can be related to translational space, as these are motions of the same kind as translational motion of physical objects, differing only in direction. This is not true in the realm af the simple basic motions that we are now considering. The oscillation is not at all similar to the scalar progression from which it is derived. It is motion of an entirely different character, involving some important factors such space or time displacements and reversals of direction that are totally absent in undifferentiated space-time.
Inasmuch as the progression of the oscillating unit is merely outward, without an inherent vectorial direction, the direction with respect to a three-dimensional coordinate system will be determined entirely by chance. Consequently, if a number of such units originate simultaneously at the same spatial location they will be distributed uniformly over all directions. The first observable feature of the theoretical universe is therefore a phenomenon in which oscillating units originate at various spatial locations and move outward from these locations in all directions at a constant unit speed, the path of movement taking the form of a sine curve.
As the various features of the theoretical universe are developed step by step from the basic postulates of the system, we will want to compare these theoretical features with the corresponding features of the observed physical universe, partly as an aid toward a clear understanding of the various points brought out in the development, but more particularly as a demonstration of the fact that the theoretical universe is a true and accurate representation of the actual physical universe. The first issue that we encounter in this connection is the matter of identification. The features of the theoretical universe emerge from the development without labels, and before we can demonstrate that some particular one of these features—the oscillating unit that we have just been discussing, far example—is identical with the corresponding feature of the observed universe, we must identify that corresponding feature. The names of the various features are purely arbitrary, and it is therefore impossible to establish a direct correlation with a name, but we can describe the observed feature corresponding to that name, and we can also describe the theoretical feature in terms of the manner in which that feature would manifest itself to observation. If an identification is correct, the two descriptions will coincide. In any event, the identification is self-verifying, as any error will quickly show up as a contradiction or inconsistency.
Ordinarily the identification is practically self-evident. It is obvious, for instance, on the basis of the description that has been given, that the oscillating units we have been discussing are photons. The process of emission and movement of these photons is radiation, and the space-time ratio of the oscillation is the frequency of the radiation. The one-to-one space-time ratio of the outward progression is the speed of radiation, more familiarly known as the speed of light. One of the things we can expect an accurate new theory to do is to clear up the major confusions and uncertainties previously existing in the fields to which it applies, and it is evident that the foregoing explanation accomplishes this result for radiation. The dual aspect of radiation, in which the photon sometimes seems to act as a particle and sometimes as a wave, has been a particularly baffling problem, but it can now be seen that there is a very simple reason for this duality. The photon acts as a particle (that is, a discrete unit) in emission and absorption because it is a discrete unit. It travels as a wave because the combination of its own inherent oscillating motion with the linear outward motion of the space-time progression takes the form of a wave. The characteristics that could not be reconciled as long as it was thought that we are dealing with the photon alone, and have confronted us with a paradox that, as James B. Conant once said, “seemed intolerable” in the days before we “learned to live with it,”13 can readily be understood as soon as we recognize that what we are actually observing is not the photon alone, but the photon plus the space-time progression.
A still more difficult problem in the radiation field has been the question of a medium. There is ample evidence to show that radiation travels as a system of waves, but no one has been able to conceive of any way in which a wave-like motion can be propagated without a medium or something with the properties of a medium. However, all attempts to detect the existence of a medium have failed, and the theorists have therefore resorted to the same device that primitive man employed whenever he encountered a problem that was beyond his capabilities. They have invented a demon to take care of the matter, a hypothesis that cannot be refuted because it cannot be tested: the hypothesis that space itself has the properties of a medium. The development of the Reciprocal System of theory resolves this issue in an unexpected, but very simple, way. It shows that no medium is necessary because radiation, as such, does not actually move at all. Each photon remains in the same absolute location, the same point in the stream, in which it originates, and it is carried outward by the progression of space-time.
The stream in which the photon-emitting object is located, the datum with respect to which an object without independent motion is stationary, may, and usually does, include a component other than the progression. Thus the frequency of the radiation, as received, and the direction from which it is received, vary with the relative motion of the emitter and the receiver. The speed of travel, however, remains constant at unity.
In approaching the question as to why this speed, the speed of light, should remain constant irrespective of the reference system, we are entering an area which has an unusually high emotional content for a scientific issue. The prevailing theory, relativity, won general acceptance only after overcoming strong opposition, based partly on scientific grounds, such as the existence of “paradoxes” which can be explained away only by making use of some expedients of a rather dubious character, but more particularly on the fact that this theory conflicts with some firmly held intuitive concepts. Because of the nature of most of the opposing arguments, the controversy between the supporters and the opponents of relativity, like the analogous controversy over evolution, took on the appearance of a contest between science and non-science. As a result, the present tendency in scientific circles is to close ranks and to assert dogmatically, with Heisenberg, that
It (relativity) has become a permanent property of exact science just as has classical mechanics or the theory of heat.14
even though those who consider the situation logically and dispassionately are more likely to arrive at a conclusion similar to this from Peter G. Bergmann:
Like all other theories of nature, relativity is certain to require modification, and perhaps even complete replacement, as man’s actual knowledge of the physical universe increases.15
In view of the emotional atmosphere that surrounds this subject, it seems advisable to interrupt the development of theory long enough to make it clear just what this development is designed to accomplish, and how it is related to existing theories in the fields that it covers. As explained earlier, all of the conclusions reached herein are purely theoretical. It is not contended that they are logical consequences of observed relations in the areas to which they apply, the kind of a foundation on which scientists normally try to erect their theories. The conclusions reached herein are wholly creatures of theory, necessary and unavoidable consequences of the postulated properties of space and time, and they are completely independent of anything that we may happen to know about the actual physical universe. But even though the new theoretical system has not been derived from observational data, comparisons with established physical facts have shown an exact correspondence between theory and experience wherever conclusive correlations have been possible, and we are therefore justified in asserting that the purely theoretical universe defined by the consequences of the postulated properties of space and time is a true and accurate representation of the actual physical universe.
What we are undertaking to do with respect to each individual feature of the universe that we discuss is to verify this general statement in application to the particular case; that is, to show that the theoretical conclusions regarding this feature are an accurate representation of that feature, or, where little is known about the phenomenon in question, are consistent with that limited amount of knowledge. We are not undertaking to show that existing theory in the area is wrong, or even to show that the new theory is better than the one now accepted (if any). Such issues are irrelevant.
For example, the first physical process that emerged from the theoretical development was the space-time progression. Obviously, this provides an immediate explanation for the recession of the galaxies and the speed of the most distant. In Chapter IV a further development of the theory will explain why the recession speed of the closer galaxies is lower. Here, then, the new theoretical structure gives us a picture of the recession phenomenon that is consistent with everything that we know about the physical situation. It thus qualifies as an accurate representation of the observed recession phenomenon. This is what we have undertaken to produce, and anything further is superfluous. No purpose is served by debating the relative merits of the new theory and its predecessor, a question which, as matters now stand, would have to be decided on the basis of nonscientific preferences and prejudices, inasmuch as both theories are in agreement with the very few facts that are available from observation.
This point that more than one—sometimes many more than one—theory can be in full agreement with experience in a limited physical area is something that is too often ignored in present-day practice. As Professor Herbert Dingle puts it, “A theoretical demonstration that the theory contains no internal contradictions—that it could be right—has frequently been regarded as a proof that it is right.”16 This logical fallacy is especially in evidence in the attitude toward theories such as relativity to which there is a strong emotional attachment. It is a well-known fact that there are other explanations that are equally as consistent with the observations as relativity. “There are some other logical questions raised by the theory of relativity,” says Hesse, “because there are a number of alternative theories which all appear observationally equivalent.”17 The truth is that relativity is merely a largely arbitrary selection from among these theories.
Thus, the requirement that a theory must be consistent with the data from observation, which the new system must be prepared to meet in order to justify the claim that it is an accurate representation of the physical facts, does not include a requirement that it be consistent with relativity theory. Agreement with one of the other theories that are “observationally equivalent” would be equally satisfactory, or alternatively, a totally new explanation that meets the observational tests could be produced. The latter is what has actually happened. Development of the postulated properties of space and time leads to a theory of the composition of velocities that is fully in accord with experience, but is altogether different from anything that has appeared heretofore.
The essential feature of this new theory is the broader view of the nature of time that is implicit in the concept of a universe of motion. The conventional view of time is that it is the entity that is measured by a clock, but the new theory based on the “motion” concept says that the clock measures only the time progression, and not total time. This is equivalent to the kind of a space measurement that we would make in a distant galaxy if we measured only the movement of an object due to the recession and did not recognize any motion of the object in the three-dimensional space occupied by the galaxy. For present purposes this is all we need, or can use, just as clock time was adequate for our purposes when we were not dealing with any very high velocities. But if we improve our instruments to the point where we can detect fast-moving objects within the distant galaxy, we will find that the recession alone does not give us the correct measure of the change in position of such an object. To get the right answer we will also have to take into account the movement in three-dimensional space, the coordinate space, as we will call it.
By reason of the reciprocal relation between space and time, the same situation exists with respect to time measurements. In the ordinary affairs of our daily life the only time that we need to take into consideration is clock time, because changes of position in what we may call coordinate time, the time analog of coordinate space, are negligible. But at high velocities the motion in coordinate time becomes an important factor. At the velocity of light, motion is taking place in time at the same rate as in space: a one-to-one ratio. In Figure 1, two photons are emitted simultaneously from point O in opposite directions. At the end of one unit of clock time they have reached A and B respectively. According to Newton, the relative velocity is the separation that has taken place in space, two units,
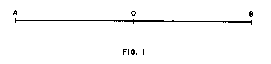
divided by the elapsed clock time, one unit, the result being two units of velocity. But the experimental evidence indicates that if this relative velocity could be measured it would be found to be one unit, not two units; that is, the velocity of light is always unity, irrespective of the reference system.
The experimental discovery of the constant velocity of light invalidated Newton’s relations in application to high velocities, and made it necessary to develop a new theory. To Einstein, working within the context of a universe of matter, and committed to the proposition that time is something that is measured by a clock, there appeared to be only one answer: abandoning the idea of absolute magnitudes and substituting the concept of magnitudes that are inherently variable. His solution for the problem of Figure 1 was to postulate the constant velocity of light, and to assert that the space and time magnitudes are automatically modified to the extent necessary to produce this result.
Einstein realized… that the only possible way in which a person moving and a person standing still could measure the speed (of light) to be the same was that their sense of time and their sense of space are not the same, that the clocks inside the space ship are ticking at a different speed from those on the ground, and so forth. (Richard Feynman)18
The findings of this work now show that Einstein’s hypothesis is not “the only possible way” to take care of the problem. It may have been the only possible way that the problem could be solved within the confines of the artificial restrictions that Einstein placed on the situation—that is, within the context of a universe of matter and without modifying the accepted concepts of the nature of space and time—but this point is irrelevant. In the context of a universe of motion, there is another way. The development based on the “motion” concept has revealed the existence of an aspect of the universe hitherto unknown—coordinate time—and all that is necessary in order to solve the problem of the composition of velocities is to take the coordinate time into account in the proper manner.
In Fig. l, what is required is to realize that from the standpoint of photon A, only the space OA and the corresponding time OA are components of the space-time progression that is responsible for the motion of A. The clocks therefore register only the time OA. The space OB does not enter into the progression of A; it is another unit of space, a unit of coordinate space, as has always been recognized. The point of the new explanation is that the same is true of the corresponding time ob. This is another unit of time, and with respect to photon A it is a unit of coordinate time, a unit that is not involved in the progression of A.
In the context of a stationary temporal reference system, both oa and ob are intervals in coordinate time. But OA is the time interval through which the progression carries photon A while it is moving from O to A in space, and this is the interval that is registered by clock A. The time interval ob through which photon B moves coincidentally has no relation to the progression of photon A, and it is not registered on clock A. Conversely, clock B registers the time interval ob, which is the time involved in the progression of photon B, but not the time interval OA. Thus both clocks register the same amount of time, as they must, since the speed of the progression is always unity, but neither registers the full time interval by which the two photons are separated when they reach spatial locations A and B respectively. At this juncture, where they are separated by two units of space they are likewise separated by two units of time, and the equation of motion is 2/2 = 1, which agrees with the observations. At lower velocities, the coordinate time increment, the time interval that is not involved in the progression and hence does not register on a clock, is smaller, and at the ordinary velocities of everyday life it is negligible. There are some observed physical phenomena, however, in, which the effect is appreciable, and in application to these phenomena the coordinate addition to the clock time produces the same mathematical results as the theory of relativity. These mathematical results are frequently portrayed in current literature as “proofs” of the validity of the relativity theory, but this is the kind of non sequitur mentioned by Dingle: accepting a showing that the theory could be right as proof that it is right.
Such loose reasoning is always unsound practice, but it is even more illogical than usual in the case of the claims made for special relativity, as the mathematical relations from which the results have been obtained, the Lorentz equations, were not even derived from the relativity theory. They antedated the theory and are independent of it. Einstein’s contribution was to furnish a plausible explanation of these empirically discovered relations, one that had no more scientific foundation than the explanations previously available, but was philosophically more acceptable to most scientists. The observed conformity of various phenomena with the mathematical relations does not confirm the validity of Einstein’s explanation. It merely means that any one of the many mathematically equivalent theories relativity, the several “observationally equivalent” theories mentioned by Hesse, or the theory described herein, based on the concept of motion in time—could be correct. The difference between these theories is merely in their respective explanations of the origin of the observed effects.
Here again, then, the new system does its job; it produces a true and accurate representation of the physical facts. Any question as to which is the “better” theory is meaningless in this connection. The new theory does all that can be expected of it; all that any theory can do. It is worth mentioning, however, that the discovery of the existence of a second time component that modifies the clock time under certain circumstances reveals why it has not been possible to extend the special theory to the general situation of non-uniform motion. A system of n components can be represented by n/1 variables only where some regularity permits expressing the extra component in terms of one of the others. For example, if we knew nothing of the property of direction, but could measure speed and also the progress toward a certain designated point, and we were trying to express one of these quantities in terms of the other, we would be successful in certain cases where there is a definite relation between the two, as in uniform linear motion, but we could not formulate any general relation, simply because there is no such relation. Before we could set up anything applicable to the general situation we would have to discover the property of direction, and start measuring vectorial quantities. Discovery of the additional time component is, in a sense, comparable to the discovery of the property of direction.
No doubt many will find it difficult to believe that any significant basic feature of the universe could still remain undetected after physical science has attained as high a stage of advancement as that which currently prevails. But it should be remembered that all of the results thus far obtained by physical science have been based on the concept of a universe of matter, which is now definitely known to be erroneous, and what has been accomplished to date therefore represents the best that science has been able to achieve in working from the wrong premises. This past experience does not in any way delimit the potentialities of a correct theory. Coordinate time is only one of a number of hitherto unknown physical features of prime importance that have been brought to light by the development of the details of a universe of motion. The previous inability to detect these phenomena is simply part of the price that science has paid for building its structure of theory on an erroneous basic concept.
