CHAPTER IX
Quantitative Verification
In the preceding pages it was shown that if we accept the proposition that the basic constituent of the universe is motion rather than matter, the true nature and properties of space and time can be readily determined. It was then demonstrated that a detailed development of the necessary consequences of the existence of entities with such properties produces a potentially complete theory of the universe. An immense number of qualitative and quantitative correlations between this theory and the results of observation have been carried out in basic physical areas without encountering any negative results, and this exact agreement with experience justifies the conclusion that the new theoretical structure is a true and accurate representation of physical existence in the areas that have been examined. Inasmuch as this theoretical structure is a fully integrated unit derived deductively from a single set of premises, verification of its validity in some areas is a verification of the validity of the structure as a whole. The conclusions that can be drawn from this general physical theory with respect to astronomical issues should therefore be equally as accurate as those physical conclusions that can be more easily and completely verified.
As has been brought out in the previous discussion, this presumption as to the accuracy o# the theory in application to astronomy is substantiated by a complete qualitative correspondence between the theoretical and observed characteristics of the various astronomical phenomena under consideration in this work: pulsars, quasars, white dwarf stars, galactic explosions, supernovae, the recession of the galaxies, etc. As a matter of gilding the lily, so to speak, we would like to complete the picture by making some extensive quantitative correlations similar to those that have been carried out in such areas as the properties of matter. Unfortunately, the observational data of a nature suitable for this purpose are as yet rather limited. In the case of the pulsars, the only reliable quantitative data thus far available are those relating to the pulsation periods and their characteristics. Measurements of other quantities such as “dispersion,” for instance, are subject to considerable uncertainty, not only as to the accuracy of the reported values, but even as to the significance of the quantities being measured. No one is quite certain whether the “dispersion” measurements actually tell us anything.
The situation with respect to the quasars is somewhat better, but before any real progress could be made in this area it was practically essential to have some definite mathematical verification of the theoretical conclusions with respect to the nature and composition of the quasar redshifts. As mentioned in the introductory chapter, some recent work by Halton Arp of the Mt. Wilson and Palomar Observatories has now put us in a position where a conclusive quantitative verification of the redshift theory is feasible, and once this point is established, the door is open for many further quantitative correlations.
The theoretical development outlined in the preceding pages indicates that each of the oldest and largest galaxies ultimately undergoes a series of explosions in which it ejects fragments that, for a time, emit relatively large amounts of radiation at radio frequencies. Each ejection consists of two components: one fragment—small galaxy—that is quite normal, aside from the strong radio emission in its early stages, and the other, the quasar, a fragment of similar size that has some characteristics which are highly abnormal in the context of the material universe, because, according to the findings of the theoretical investigation, it is ejected with a speed greater than that of light. Like the normal recession, in which a galaxy is progressing outward at the speed of light but at the same time moving inward gravitationally, so that the net speed is less than that of light, the speed generated by the galactic explosion is a recession, a scalar outward motion, and it, too, is reduced to lower levels, for a finite period of time, by gravitation. As explained in detail in the preceding chapter, the explosion speed increases the redshift of the quasar by an amount 3.5 z½ where z is the normal recession redshift corresponding to the location of the quasar.
What Dr. Arp has accomplished is to identify certain instances in which there is evidence of a physical relationship between a quasar and some normal objects. Inasmuch as these physically related objects must be situated at approximately the same spatial location, this enables us to determine the magnitude of the component of the quasar redshift due to the normal recession, and hence to verify the theoretical relation between the excess redshift and the normal redshift.
Obviously, the existence of any demonstrable relation of this kind invalidates all of the explanations of the quasar redshift that are currently being given consideration in astronomical circles. Identification of the normal recession redshift as a minor component of the total shows that the prevailing view attributing the entire redshift of the quasar to the recession is incorrect. At the same time, the fact that the excess redshift is a specific function of the normal redshift rules out gravitation and other explanations of a non-recession nature. The further demonstration that an analysis of the observational data confirms the theoretical 3.5 z½ relation between excess and normal redshift goes a step farther and shows that the theoretical explanation is correct, thus adding a key item of quantitative evidence to the many qualitative indications of the validity of the theoretical development.
The associations identified by Dr. Arp are pairs of radio emitters located on opposite sides of “peculiar” galaxies that show visible evidence of internal disturbance. His theory is that the radio objects were ejected simultaneously in opposite directions from the central galaxy and have moved out to their present positions in the intervening time since the explosion. In some instances, more than one such pair is associated with the same central galaxy, and the assumption here is that the explosion process has been repeated. Where this has occurred it may not always be possible to correlate the product with the particular explosion, and a product of explosion I might easily be paired with the product of explosion II or explosion III. For present purposes this is immaterial as long as the kind of components required for the analysis are present, as the difference in current position between the products of successive explosions is not sufficient to introduce anything more than minor deviations from the theoretical redshift values.
In order to carry out the correlation, however, it is necessary to know the redshift of the quasar and that of at least one of the other members of the association, and any group for which this minimum amount of information is lacking must be excluded from the analysis. Any of the identified associations that contain no quasars are of no value for our purposes, regardless of the reason for their absence, and also have to be excluded. After these exclusions, which involve about half of the groups identified by Arp in 1967, there are ten associations available for analysis.
If each of these associations actually consists of a central galaxy and two or more fragments ejected from that galaxy, as Arp concludes, then all members of this association should occupy adjacent locations in space, and their recession redshifts should be approximately equal, differing only by the amounts due to the relatively small change of position since the explosion, random motion, etc. Disregarding these minor factors, a three-component association should theoretically consist of a central galaxy with redshift z, an ordinary radio galaxy with redshift z, and a quasar with redshift z +3.5 z½. In any case where at least one of the associates has been correctly identified, and the redshifts have been measured, we are therefore able to test the accuracy of the theoretical relation by computing the value of the quasar redshift corresponding to the appropriate value of z, and comparing it with the observed quasar shift.
Before proceeding with the comparison it will be advisable to take note of some of the conditions that must be maintained in order to assure the validity of the conclusions that are reached. If we were working with data of unquestionable reliability, this would present no problem. We would simply go ahead with the calculations without further ado. But the task that Dr. Arp has performed is one of extraordinary difficulty, and it is wholly unrealistic to expect that all of his results are correct. Indeed, the majority of his colleagues seem unwilling to concede any validity to these results, as is evident from the general preference for the “cosmological” explanation of the origin of the quasar redshifts, which attributes them entirely to the normal galactic recession and thus denies the existence of the second component that must exist if Arp’s associations are physically real. We are therefore in a position where we have a double task: we must verify our basic data in the same operation by which we verify the theoretical redshift relation from these data.
In order to deal with what may be a mixture of correct and incorrect data, it is necessary to rely upon probability considerations. If the quality of the data available for analysis is poor, it might not be possible to reach any definite conclusions at all by these means, as the results that we obtain may not differ enough from random probability to be statistically significant, but if a reasonable percentage of Arp’s identifications represent actual physical associations some meaningful answers can be obtained. Inasmuch as the theory being tested calls for the existence of a specific mathematical relation, any degree of conformity with that relation exceeding random probability is evidence in favor of the theoretical conclusion. A high degree of correlation much in excess of random probability is tantamount to proof, not only of the validity of the theoretical relation but also of the validity of the data that are in agreement with the theory.
The nature of the process is such, however, that some very stringent precautions are necessary in order to prevent introducing some kind of bias that would invalidate the probability argument. The most essential requirement is that the data must be random with respect to the point at issue. As the textbooks on probability emphasize, the probability principles and arguments are applicable only to random phenomena. One of the best ways to insure the necessary randomness is to utilize data that were previously compiled for some other purpose. If Dr. Arp had undertaken his work with the ultimate objective of making some such correlation as that which we are now contemplating, we could never be sure that selection effects were entirely absent, and hence the results would always be subject to a corresponding degree of uncertainty. But where his world was done with one purpose in view, and we are taking advantage of it for a totally different purpose, randomness of the data, with respect to the object of our inquiry, is achieved almost automatically.
One further requirement that must be observed, however, if conclusions based on probability considerations are to be beyond reproach, is that the data must be homogeneous, because unless they are homogeneous they cannot be completely random. We must therefore see that our information has all been gathered on the basis of the same set of criteria and the same processes of judgment. This means that where a process of selection is involved, we must utilize the data in the original form and exclude later additions or modifications, as it is practically impossible to maintain the original selection criteria unchanged over any substantial period of time. Even if a conscious effort is made to avoid such changes, events taking place in the interim, and the natural evolution of thinking in the course of time, will alter the criteria in ways that are difficult to identify. For this reason the comparisons in this chapter are all based on Arp’s first extensive set of results, published in 1967.38 Subsequent to this publication he modified some of his original groupings and identified a considerable number of additional associations, some on the basis of the original considerations, and some on other grounds. But we cannot use this additional material in conjunction with the original, because if we do, we no longer have the homogeneous set of random data that is required to assure the validity of our probability arguments. The additional material can, of course, be used for other similar studies, and the results thereof are entitled to the same kind of consideration as the results of the present analysis, but it must be separate consideration.
It may soon be possible to duplicate the results that we have obtained from an analysis of Arp’s original work, which was confined to objects included in the 3C (Third Cambridge) catalog of radio sources, by a similar study of another list of associations that he identified by an extension of his work to the objects listed in the Parkes (Australian) catalog, but for the present the redshifts needed for the Parkes study are not available. Although the measurement of redshifts of the radio emitters is being pursued diligently, there has been no reason, so far as those engaged on this work are concerned, for giving preference to the objects included in Arp’s identifications, and the information required for analysis of the Parkes groups has been accumulating rather slowly. In fact, the necessary measurements are available for only two of these groups as yet. The results that we obtain from these two associations will be presented along with those of the principal study as an indication of what may be expected when more of the redshifts of the Parkes objects have been measured.
Other additions or modifications can similarly be utilized for separate studies where enough information of a homogeneous nature is available, but they cannot legitimately be combined with the original set of data. For example, Dr. Arp has found that there are several quasars located on a straight line that apparently proceeds from the galaxy NGC 520, and he considers this as evidence of physical association. But an identification of association of quasars or other objects based on linear alignment is something quite different from an identification based on the presence of two radio emitters on opposite sides of a “peculiar” galaxy, and we are not justified in taking it into account when we are undertaking to apply probability principles to an assessment of the validity of identifications made on the latter basis. Whatever conclusions we may draw from the NGC 520 alignment are separate and distinct from those derived from the study of objects from the 3C catalog selected on an entirely different basis.
It should be noted that in cases of this kind, where we are dealing with data of unknown validity, a negative result from one set of data does not invalidate a positive result from another set of data. The reason is that a positive result is more comprehensive; it contains more information. Such a result tells us that both the theoretical relation that is being tested, and the portion of the data that conforms to that relation, are correct, whereas a negative result only tells us that either the theory or the data must be wrong. Where we have a positive result on the basis of one set of data—a definite indication that the theory is correct—and a negative result on the basis of a second set of data—an indication that something is wrong—the logical inference is that the error lies in the second set of data.
With the benefit of the foregoing understanding as to what we propose to do and how we propose to go about it, we may now proceed to an examination of the twelve associations from Arp’s 3C and Parkes studies that are available for this purpose. On beginning this
| Association Number |
Quasar Redshift |
Basis of Calculation |
Excess/z? |
|---|---|---|---|
| 134 | 0.158 | C | 2.78 |
| 160 | 0.320 | C | 3.41 |
| 125 | 0.595 | C | 3.31 |
| 148 | 0.734 | C | 3.76 |
| 201 | 1.037 | R | 3.56 |
| 139 | 1.055 | R | 3.31 |
| 5055 | 1.659 | R | 5.59 |
| Excluded | |||
| 5223 | 0.849 | C | 5.3 |
| 143 | 1.063 | C | 9.1 |
| 197 | 2.38 | C | 16.7 |
examination, the first thing that we encounter is the necessity of some further exclusions, because the theory itself identifies some of the presumed associations as incorrect, and hence these associations cannot provide any comparisons of theory with observation. Where the theory asserts that no agreement is to be expected, a demonstrated lack of agreement is meaningless.
Dr. Arp says that he does not expect to be able to identify the central “peculiar” galaxies beyond a recession of 10,000 km/sec.39 The quasar 3C 254, with a redshift of 0.734, of which 0.039 is the normal recession, is theoretically receding at slightly over this limiting recession speed, and is therefore approximately at the point beyond which the theoretically correct central galaxy is unobservable. According to the theory, then, any identification of a central galaxy with a quasar appreciably more distant than 3C 254 (in association 148) is prima facie wrong, and a comparison of the redshifts has no significance. We can test the theory only by checking the correlation in those cases where the theory says that there should be an agreement. On this basis, the only significant correlations with the central galaxy redshift are the first four in Table II. In all of these cases the theoretical and observed values show a satisfactory agreement. (The ratio 2.78 for association 134 would not be satisfactory at a higher z value, but obviously the incidental items previously specified have a higher proportionate effect where the recession is so small.)
Beyond the point where the correct galaxy of origin becomes unobservable it is still possible that the radio galaxy associated with a particular quasar may have been correctly identified, as the radio galaxies can be detected at distances well beyond those at which the features distinguishing a “peculiar” galaxy can be recognized. The correlations in our analysis have therefore been made on the basis of the radio galaxy, if the necessary redshift measurement is available, rather than the central galaxy, far all distances greater than that of association 148, as indicated by the symbol R in the third column of the table. Here, again, however, there is an upper observational limit. It is somewhat indefinite, because of the wide range of emission energies, but the available evidence indicates that only the exceptional radio galaxy can be detected at the distance corresponding to the theoretical location of the quasar 3C 280.1 in association 5055. The legitimacy of this association is therefore open to question. Since we must exclude associations 5223, 143 and 197, together with 908 from the Parkes catalog, on the grounds previously cited, this questionable case, number 5055, is the only one in the entire list where there is a lack of agreement with the theory. All of the other associations in which the observed relation between quasar redshift and normal recession redshift could agree with the theoretical relation do show such an agreement.
The relevant data from Table II are shown graphically in Figure 5. Each plotted point on the graph indicates the relation of the excess redshift of the particular quasar, the amount by which the quasar redshift exceeds that of a galaxy with which it is presumably associated, to the redshift of that associated galaxy. The relation to which these points should theoretically conform is shown by the diagonal line. If current astronomical opinion is correct, and the redshifts of the quasars are due to the normal recession alone, there will be no definite relation between the quasar redshift and that of the object or objects which Arp has grouped with it, and in that event the plotted points will scatter randomly, not only over the area of the graph as shown but also over a much larger area above it, extending up to values of 30 or more, as can be seen from the figures in the “excluded” group of Table II. The same will be true if the associations are real, but, as Arp himself suggests, the excess redshift is due to some cause other than motion, and hence not directly related to the normal recession.
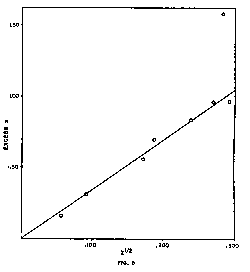
But they are definitely not random. On the contrary, 6 of the 7 points (plus the one from the Parkes survey) fall essentially on the theoretical line; that is, within the margin that can be attributed to the distance the ejected objects have moved since the explosion, to random spatial motion, and other minor effects. The probability that 6 of these 7 points would fall on a straight line merely by chance is extremely remote; the probability that 6 out of 7 would fall on a straight line passing through the origin of the graph by pure chance is negligible; and the probability that 6 out of 7 would by chance fall on a straight line coinciding with a theoretically derived relationship is hardly even conceivable. The results of the test are therefore conclusive. They constitute a positive verification of the theoretical 3.5 z½ value of the excess quasar redshift.
Inasmuch as only one of the associations from the Parkes catalog qualified for inclusion in the test, the result in this case is not of any great significance, but the calculated ratio is 3.55, in full agreement with the theoretical value. To the extent that we are justified in taking the Parkes data into account, therefore, they support the conclusions reached by analysis of the 3C redshifts.
In addition to confirming the validity of the theoretical explanation of the quasar redshifts, the test results also prove that Arp’s identification of the central galaxy from which the quasar was ejected is correct in all cases where the central galaxy is near enough to be observable. Beyond this range, he has correctly identified the radio galaxy associated with the quasar (either specifically or as one member of a multiple association) out to the distance where detection of any but the most powerful radio galaxies becomes difficult. In other words, at least one of the associates of the quasar has been correctly identified in all cases (with only one possible exception) where these associates could have been identified. In almost all instances where our analysis indicates that the central galaxy, or some other member of an association, has been incorrectly identified, the reason is that the correct object is too far away to be recognized.
Further confirmation of the quasar theory, highly significant because it involves a decidedly unconventional aspect of the quasar motion, can be obtained from a calculation of the speeds of the radio galaxies in those associations where all three components central galaxy, quasar, and radio galaxy have been clearly identified. There are only three cases that definitely fall in this class, as the radio galaxy in 148, the fourth of the associations within the 10,000 km/sec range, is unidentified optically, but its approximate location is known from the radio observations and the 148 system can therefore be included in the study. We can determine the theoretical spatial speed of the quasar in each of these associations from its redshift, and the ratio of the quasar speed to the speed of the radio~ galaxy from observation of the distance that each has moved since the explosion. From these two values we can then calculate the speed that the radio galaxy must have to be consistent with the theoretical speed of the quasar. If this calculated speed falls within the range in which we know the actual speed must lie, we have confirmed the theory of the spatial speed of the quasar, strange as that theory may seem in the context of conventional thought.
An approximate value of the actual speed of the radio galaxy can be obtained from a consideration of the initial speeds of its constituent stars. Just before the ejection, the individual stars in the center of the galaxy of origin are moving in random directions. The force of the explosion then superimposes on these random motions a component of motion in the outward direction. Most of the stars are thus accelerated to ultra high speeds and become part of the quasar, but some fail to attain the speed of light, and these slower stars are ejected in space as a radio galaxy. The average outward speed of these stars at the time of ejection determines the speed at which the “star gas” aggregate moves outward, and since the initial speeds are
| Association Number |
Excess Redshift |
Spatial Speed |
Distance Ratio |
R.G. Speed |
|---|---|---|---|---|
| 134 | 0.155 | 0.845 | 0.73 | 0.62 |
| 160 | 0.312 | 0.688 | 0.91 | 0.62 |
| 125 | 0.566 | 0.434 | 1.35 | 0.59 |
| 148 | 0.695 | 0.305 | 2.57 | 0.78 |
the tail of a probability curve in the range from 1.00 downward, the average should be somewhat above 0.500 and nearly the same in all cases. This is the requirement that the results of the theoretical calculations must meet in order to validate the theory.
According to this theory, the spatial component of the speed of the quasar, the component that manifests itself by changing the quasar position in space, is that portion of the speed which is required to overcome gravitation. In terms of redshift (numerically equal to the speed) it is the difference between 1.00, the speed of light, and the excess redshift of the quasar, as previously defined. The theory thus predicts a rapid decrease in the spatial speed of the quasar with increasing distance. This is completely at odds with current ideas as to the nature of motion, inasmuch as it implies that a constantly increasing proportion of the speed generated by the galactic explosion and reflected in the quasar redshift has no effect toward changing the position of the quasar in space. The results of the calculations summarized in Table III, which confirm this theoretical prediction, therefore provide some strong reinforcement for the conclusions reached in the analysis of the relation between the recession redshift and total redshift of the quasar.
Column 2 of the table gives the excess redshift of the quasar in the association identified in column l. According to the theory, the spatial speed of the quasar, the rate of change of position in space, is the difference between the excess redshift and unity, as shown in column 3. On the basis of measurements by Dr. Arp, we find the ratios of the apparent distance of the radio galaxy from the central galaxy to the corresponding distance of the quasar from the central galaxy to be as indicated in column 4. Inasmuch as the distance traveled since the explosion is proportional to the spatial speed, the figures in column 4 also represent the relative spatial speeds of the radio galaxy and the quasar. Multiplying the spatial speed of the quasar (column 3) by the ratio of the speeds (column 4) then gives us the speed of the radio galaxy (column 5).
These results in column 5 meet the requirements set forth earlier in the discussion; that is, they arrive at essentially the same speed for all four radio galaxies (if we make an allowance for the lack of certainty in the position of the radio galaxy in association 148) and this calculated speed is within the limits that we can establish from more direct considerations. Furthermore, a very wide range of quasar speeds is included, as the theoretical spatial speed of the quasar 3C 273 in association 134 is twice that of 3C 345 in association 125, and almost three times that of 3C 254 in association 148. The downward trend in quasar distances as the speed increases is unmistakable.
As brought out in the theoretical discussion in Chapter VIII, an important consequence of this rapid decrease in the spatial speed of the quasars is that beyond an explosion speed of 1.00, equivalent to a recession redshift of approximately 0.08, the spatial speed of the quasar, relative to the location from which we observe it, is zero, and from our point of view it remains at its location of origin. This means that from 1.00 to the upper limit of 2.00 (2.326 total redshift) half of the quasars are behind the galaxies from which they originate, and are therefore not recognizable as quasars. As indicated earlier, the number of visible quasars is theoretically proportional to the 1.5 power of the distance. If we plot N against d1.5 for any random sample of the quasar population we should therefore obtain a straight line from zero to some number n at explosion speed 1.00, at which point there should be a sharp break to another straight line that reaches 1.5 n at the point on the graph corresponding to explosion speed 2.00. In Figure 6 the quasars listed in Table 3.1 of the Burbidges’ book Quasi-Stellar Objects, which includes all those for which redshifts were available at the time of publication, have been taken as the random sample. The curve is obviously in full agreement with the theoretical pattern, and the agreement is especially significant because the pattern is an unusual one. Together with the data presented in Tables II and III, this confirmation of the decrease
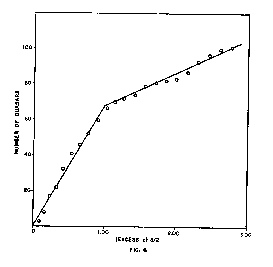
in the number of visible quasars beyond 1.00 should establish the nature of the quasar motion and redshift on a firm basis.
Another independent confirmation of the quasar theory is supplied by observational data that verify the theoretical conclusion that the quasar radiation is distributed two-dimensionally and therefore varies in proportion to the inverse first power of the distance rather than following the inverse square relation that applies to phenomena originating in three dimensions. A direct comparison between quasar distance and luminosity is rather difficult to interpret because of the wide range of inherent luminosities, but where there are a number of quasars at approximately the same distance, the average luminosity of the group should approximate that of a quasar of average inherent luminosity, and by making our comparison on the basis of these group averages we can, to a large extent, eliminate the effect of the individual variability.
If we start at 0.200 (thereby excluding the quasar 3C 273, for reasons which will become apparent in Chapter X) and group the quasars from the Burbidge Table 3.1 in 0.100 redshift intervals, with some extension of the interval at the very high redshifts where necessary to keep the minimum number at 5, we obtain groups of from
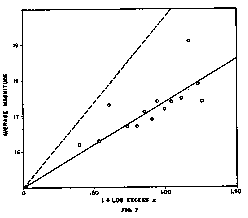
5 to 10 members. A plot of the average magnitude against the logarithm of the average excess redshift of these groups then gives us the results shown in Figure 7. The solid line in this diagram is the location of the first power relation between luminosity and excess redshift, while the broken line shows where the plotted points would fall on the basis of the inverse square relation. The verdict is clear and unequivocal: the luminosity of the quasars is inversely proportional to the first power of the quasar distance, not to the second power.
Here in this chapter is the quantitative evidence that confirms the theoretical picture of the quasars developed in Chapter VIII. We have already seen that the conclusions reached in that development are in complete qualitative agreement with the observations; now we find that the principal quantitative predictions of the theory are equally in accord with the observational data. The fact that some of these conclusions and the mathematical consequences that they predict are nothing short of outrageous in the context of conventional scientific thought makes the close correspondence between the theoretical and observed values all the more significant.
The demonstration that the quasar speed is a specific mathematical function of the recession speed verifies the theoretical conclusion that it is another motion of the recession type, subject to gravitational effects in the same manner as the recession. The theoretical assertion that this is not an ordinary spatial motion is confirmed by the mathematical proof that the greater the speed, and the redshift, of the quasar the less spatial distance it travels, until it reaches the point where the rate of change of spatial location is zero; and the theoretical assertion that it is a motion in time, with only a limited and temporary spatial effect, is confirmed by the fact that the relation between the quasar speed and the recession speed conforms to the theoretical value calculated on the time basis.
The theoretical conclusion that the motion at ultra high speeds takes place in two dimensions only enters into the relation between the explosion speed and the recession speed and therefore participates in the confirmation of the theoretical assertions regarding that relationship. Its validity is further substantiated by the analysis of the relation between quasar magnitude and distance which shows that the intensity of the radiation from a quasar is proportional to the first power rather than the second power of the distance.
The points that are thus verified are the salient features of the quasar theory as derived by development of the consequences of the postulates of the Reciprocal System. These are the quasars that exist within the framework of a universe of motion, and the agreement with experience now demonstrates that they are likewise the quasars that exist in the actual physical universe.
