From Thomas Kirk’s article “Dissecting the Birotational Photon,” in Reciprocity, XX (3), p. 14, it is apparent that his consternation over the concept of birotation put forth by me has reached alarming proportions. He hastily condemns that I am “rewriting” the Reciprocal System and “radically contradicting Larson’s development.” While I have no intention to enter into unending polemics, I am compelled to write this communication lest the uninformed misconstrue my silence as admittance of guilt. The truth is, far from contradicting Larson’s development, I am supporting it by clarifying certain aspects. Unfortunately Kirk seems to imagine that these are not clarifications but contradictions.

In the course of the study of the Reciprocal System we find that there is a class of persons who are not merely intelligent but are very intelligent—but unfortunately are not intelligent enough. Most of us, perhaps all of us, belong to this category, the average scientist included. Let me explain. It must be recognized that, over ages of tradition and habit, the human mind, in its endeavor to understand the universe, develops what may be termed a “frame of mind,” which is really a viewpoint. Every concept, old or new, is reckoned or interpreted from the background of this frame of mind. Anything that does not fit into the existing frame is summarily rejected; it cannot be felt as understood. The mind complains that “it cannot swallow it.”

1 Paradigm Shifts

In the course of the development of science any new idea or concept that may be proffered would be usually greeted with great enthusiasm and praise if that idea or concept is in conformity with the popular, prevailing frame of mind. On the other hand, once in a while there comes some scientific development which is not merely a new concept but involves a new frame of thinking. Suffice it to cite the examples of the Copernican revolution and Planck’s discovery of quanta. Such a development, though it marks real breakthrough and progress, is never readily accepted by the intelligentsia of the time. They commit the mistake of trying to understand the new concepts from the background of the previous frame of thinking whereas, in reality, they must be evaluated from the new frame engendered by the development. The result, of course, would seem to be absurd or contradictory.

In the present case, the viewpoint we have all been addicted to for the past millennia is the one that is germane to the concept of a universe of matter, namely, the inveterate habit of positing every thing as existing in a framework of space and time. We may call this the viewpoint of Container Space. With the advent of the Reciprocal System this viewpoint could be seen to be no more valid. Space and time, according to the Reciprocal System, happen to be the content of the physical universe. The majority of Kirk’s difficulties in understanding my presentation or Larson’s can be seen to stem from his inability to relinquish this slavish allegiance to the Cartesian reference frame, namely, the container space, even when the new theory demands it. We shall refer to this as the Fallacy of the Incongruous Viewpoints.

2 Direction of Rotation

Larson has shown that space, in general, is not limited to the spatial aspect of linear motion, which alone could be correctly represented in the three-dimensional spatial reference system. He points out that this reference system is deficient in more than one way. It cannot, for example, represent truly the spatial aspect of rotational motion.^1,2 The rotational space of the electron is such, for instance.³

Kirk has difficulty in following the nature of rotation. Since a rotating line segment sweeps a disk he imagines that (i) rotation is two-dimensional, and (ii) that in rotation the direction is changing continuously and hence it cannot be scalar. In item (i) he confuses between the dimensions of space and the dimensions of motion, and does not realize that one-dimensional rotation utilizes two dimensions of extension space. A quantity is one-dimensional if only one magnitude can completely specify it. Insofar as a rotation as above can be so specified by the number of revolutions per unit time, a single magnitude, it is only a one-dimensional motion. And it is also scalar if the orientation (in three-dimensional space) of its axis of rotation is not specified. From the point of view of motion it is on par with the one-dimensional scalar speed given in, say, cm/sec. The direction relevant is the direction of this one-dimensional quantity, the number of revolutions per unit time, which, however, cannot be represented in any direct way in the extension space, while the one-dimensional quantity, cm/sec, could be so represented.

The difficulty Kirk experiences in this connection is due to his unconscious, mistaken assumption that the extension space is all-comprehensive and represents rotation truly. Since the fallacy of container space regards every thing to be existing in the extension space and time, it perpetrates the belief that anything not so represented in space and time is unreal, unthinkable or non-existent. Kirk is therefore unable to see that the direction which deems it scalar or vectorial in the context of rotation is not the changing direction of its radius, but its sense of rotation. As Larson amply points out,² rotation can be represented in the conventional reference system only with the aid of an auxiliary device. For example, using the right-hand corkscrew notation we might represent a rotation by a vector of appropriate length pointing in the direction of its axis. Direction, in the context of the one-dimensional rotation then becomes the direction of this vector.

There is nothing new in this representation. We generally adopt it in common engineering practice to denote angular momenta and torques. We may call it “rotational vector.” As far as any mathematical operation on the rotational vectors is concerned they can be treated as identical to the ordinary vectors. For example, we can vectorially add two rotational vectors as we do with ordinary vectors, or decompose a rotational vector into components. However, we cannot combine ordinary vectors and rotational vectors in any operation. This is because, while ordinary vectors are correct representations, rotational vectors are artificial constructs employed by us to circumvent the limitations of the three-dimensional reference frame. Hence the rotational vector deserves a separate name, something like roctor. Their usefulness lies in the fact that within the domain of the rotational vectors we can carry out all the vectorial operations and hence while they are only artificial representations they, nonetheless, correctly represent the interrelations between them.

When we said that one could be very intelligent but not intelligent enough, we meant that one is unable to see the limitations of the viewpoint of the extension space and is unable to recognize that he is attempting to view all phenomena, whether they fit this viewpoint or not, only from such a viewpoint. Once this is realized, all the points that Kirk finds “difficult to swallow” can be understood. A re-reading of the articles on birotation without losing the awareness of this fact might now be able to convey correctly what I meant there about rotation and birotation.

3 Other Objections

The statement which Kirk attributes to me, namely, “The same scalar motion can be either translational, rotational…” etc. is really quoted by me from Larson and I gave the reference (p. 280, Basic Properties of Matter) in my article.⁴ The criticisms Kirk makes on these statements, therefore, apply to Larson and not myself. They, however, mean that Kirk has not understood Larson here. We find the cause for the mischief, once again, to be the failure to recognize the illegitimacy of the container space viewpoint.

At another place Kirk complains that I fail to elaborate my use of the word “fictitious” in connection with the space-time progression. I did not elaborate because I was only paraphrasing Larson’s explanation. Just in case Kirk could not locate the references, we quote the relevant passages here: “The sphere generated by the motion of the natural reference system relative to the point of origin has no actual physical significance. It is a fictitious result of relating the natural reference system to an arbitrary fixed system of reference.”⁵ And, “… the postulates require the existence of real units of motion, units that are similar to the units of motion involved in the progression of the natural reference system, except that they actually exist, rather than being fictitious results of relating motion to an arbitrary reference system. These independent units of motion …”⁶

Thus while Kirk has not even studied Larson properly he proclaims that I am contradicting Larson.

At another place Kirk contends that my explanation of the circular polarization entails the “modification of the atomic structure of the polarizing medium.” Of course, here Kirk was unable to distinguish between the rotation of an atom and the rotation that is the atom, and with his alacrity derides my presentation. It might be noted that the beginning of the sarcastic mode marks the ending of intelligence. If one is really concerned about truth one would make sincere attempts to follow the author, communicate with him for possible enlightenment, or discuss with others. We all have done that with Larson and with each other. Merely launching into a tirade at the slightest conceptual difficulty does not lead one very far. Patience, perseverance, and if we may point out respectfully, lack of conceit are important. They give that higher intelligence a chance to operate. Of course, in the present instance, it never occurred to me that some reader might miss the obvious and fail to discern from the context that the rotation under consideration is the rotation of the atom and not the rotation that constitutes the atom.

4 Back to the Bivector

Knowing the difficulty one may experience with the analysis of the nature of rotation, we started our original explanation with linear translational motion.⁷ We tried to show how the representation of a scalar in the conventional reference frame would be a bivector and not a vector. This explanation proceeds logically and directly from Larson’s treatment of the nature of scalar motion as against vectorial motion.⁸ Reading the passage on pp. 33-34, Nothing But Motion and then my article on “The Law of Conservation of Direction”⁷ should establish that we are only carrying out Larson’s development to its logical end, rather than indulging in “free inventions” as Kirk accuses. The analysis is next extended logically to rotation. Yet Kirk apparently tries to maintain the position that the criterion of their truth is that he should understand it. He will, of course, understand if he can pass beyond his container space frame of mind.

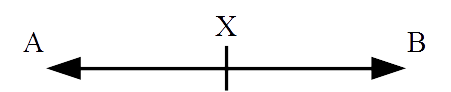
Any way we would like to try once more to see if we can be of help. Let us dwell on linear motion since this does not bring the limitation of the reference frame into picture and is consequently easier to grasp. Now the first thing we would like to emphasize is that the bivector is tantamount to a scalar. Imagine a bivector XAXB as shown in Figure 1.

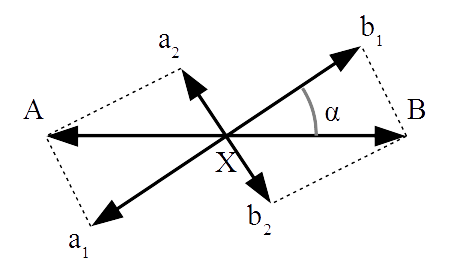
Next consider two mutually perpendicular lines making an arbitrary angle α and 90+α respectively with the line AB. Let the two components of the vector XA along these two directions be Xa₁ and Xa₂ respectively. Similarly Xb₁ and Xb₂ are the two components of the vector XB along these two directions (Figure 2). On cross-combining the components of XA and XB, such that Xa₁ is combined with Xb₂ and Xb₁ with Xa₂, we arrive at the resultants XA₁ and XB₁ as shown in Figure 3.

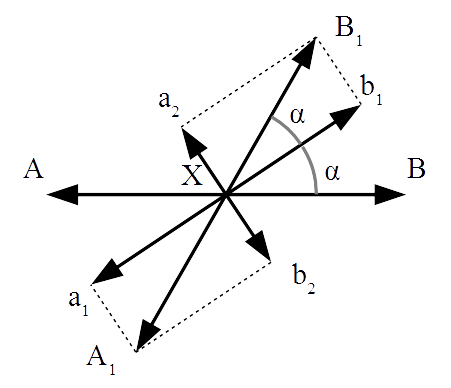
Thus the original bivector can be transformed into a new bivector XA₁XB₁ whose line of action is at an angle 2α to that of the original. Since the angle chosen, α, is totally arbitrary, this proves that the bivector XAXB is equivalent to any other bivector of the same magnitude extending in any direction (actually, bidirection) in the three-dimensional reference frame. Or what comes to the same, the bivector is tantamount to scalar. Thus when the scalar motion is placed in the context of a spatial reference frame it manifests as a bivector, and not as a vector.

It might be noted that while all the first order quantities connected with the bivector (like momenta) cancel each other out (like mv and -mv), the second order quantities remain additive (like mv² and m( v)²).

All that has been said above of the characteristics of a bivector is also true of the birotational vector (or biroctor, if one prefers to call it so). While a rotational speed has a one-dimensional magnitude and a rotational direction, and hence is a (rotational) vector, a birotational vector is a pure scalar. Hence if scalar motion manifests in a reference frame as rotation, it would do so as a birotation and not rotation. Manifestation as a rotation would entail the creation of a quantity of angular momentum not existing previously, whereas there is no such need in the case of the birotation.

Finally I have produced the proof of the pudding in a Paper entitled “Photon as Birotation” presented at the 1991 Convention (waiting to be published in Reciprocity), wherein I demonstrated how the manifold phenomena connected with radiation do follow logically from the birotational nature of the photon.

Speaking of “radically contradicting” Larson, one need only turn to page 20, Reciprocity, XX (1), Spring 1991, to find what sort of monkey wrenches Kirk is inclined to pelt at Larson.

Kirk is only an example. His difficulty is shared by all of us who fail to realize that we might be making the mistake of adopting the inappropriate conceptual frame in studying the Reciprocal System. In fact it is fatally easy to slip back into the Fallacy of the Incongruous Viewpoints and not realize it. I have separately made a careful analysis of this and other difficulties we might encounter, in a Paper entitled “The Quasar Paradox?” sent to Reciprocity for publication.

We must, however, see that Kirk has done a great service by acting unwittingly as a guinea pig inoculated with the Reciprocal System, and showing what the responses might be. These latter provide us with valuable insights as to the ways in which an intelligent, well-meaning scientist might misunderstand discussions of the Reciprocal System and end up passing wrong verdicts.

---