IX
As pointed out in Part One, any explanation of a primary physical phenomenon must necessarily rest upon assumptions or postulates of some kind, and the ultimate in physical explanation is reached when these assumptions refer to simple inherent properties of the universe, the existence of which can be independently confirmed. The origin and development of the postulates on which this work is based, and the nature of the confirmatory evidence that is available were described in a previous publication The Structure of the Physical Universe39 and the full text will not be repeated here, but it may be helpful to show briefly how the principal conceptual innovation involved in these postulates can be derived from very elementary considerations.
Let us assume that we are undertaking a study of basic physical relationships. Both past experience and theoretical considerations indicate that it is sound practice to begin with the most fundamental relation of this kind and then to build the superstructure of theories and principles on this foundation. There is, of course, no definite signpost to indicate just what this most fundamental relationship is, but few would gainsay the statement that if we wish to select the two most basic entities in the universe, the most likely candidates are space and time. The logical starting point for the study is therefore an investigation to determine the general relation between space and time.
At this point it is interesting to note that although we arrive immediately and almost inevitably at this conclusion that we should begin our study by examining the relation between space and time, this question that should logically take first place in such a project has never heretofore had any consideration as a part of the original development of any basic physical theory. Newton never even realized that there was any such relation, and in his system space and time are completely independent. Einstein ultimately picked up and utilized Minkowski’s hypothesis of a four-dimensional continuum with three space dimensions and one time dimension, but this hypothesis played no part in his original formulation; in fact, Minkowski did not even publish it until several years after Einstein’s 1905 paper. The procedure suggested by an elementary analysis of the situation therefore represents a new avenue of approach to the problem. This, in itself, augurs well for the undertaking. The odds against accomplishing anything significant by following previous routes in areas which have had as much attention as this one are tremendous, but the availability of a new approach to the problem makes the situation very much more favorable.
In order to utilize this new line of attack to the best advantage, it will be advisable to consider first the general situation in which we are examining the relation of any quantity y to any other quantity x. Let us illustrate this situation by the diagram, Figure 1, in which the values of x and y are represented in the usual coordinate manner. In the general situation there will be a known region, which we will represent by the area to the left of the vertical line a-a, and an unknown region, which will be represented by the area to the right of this line. The first step, obviously, is to determine the relation existing in the known region, which we will represent by the line O-P. The problem then reduces to a question of determining the corresponding relation existing in the unknown region.
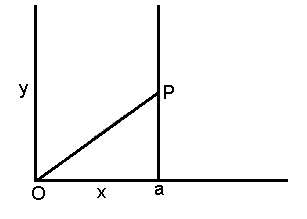
Figure 1
Since the relations in this region are, by definition, not capable of being determined in any direct manner by the means now at our command, our procedure must be to assume some relationship, then develop the consequences of this relationship, select those of the consequences which fall into the known region, and finally compare these particular consequences with the corresponding known facts. If we find an agreement, this verifies the assumption to a degree that depends on the number and variety of the correlation’s available; if there is a disagreement, the assumption is invalid and we must discard it. The problem therefore becomes a matter of deciding what assumption should be tried first.
Inasmuch as the relation in the unknown region is necessarily unknown, it could be almost anything. When we consider this general situation, however, without the distracting influences that normally interfere with a clear view of any particular physical situation, it is obvious that there is one possible assumption that is inherently far superior to all others: an assumption which has so much greater probability of being a true representation of the physical facts that we are never justified in even considering any other possibility until we have given the consequences of this assumption a complete and thorough examination. This greatly superior assumption is, of course, the hypothesis that the same relation which prevails in the known region also holds good in the unknown region; that is, it is an extrapolation from the known to the unknown.
Our analysis of the general situation along these lines thus tells us that the first move in investigating the relation between space and time in the universe as a whole should be to test the consequences of extrapolating the relation that we find existing in the known region of the universe. In this known region the relation between space and time is motion, and in motion space and time are reciprocally related. The analysis thus indicates that we should postulate a general reciprocal relation between space and time effective throughout the universe.
This reciprocal postulate is the keystone of the new system of thought of which the gravitational theory herein described constitutes an integral part, and in order to place it in the proper perspective it should be emphasized that this is essentially the only conceptual innovation introduced into physical theory by this new system. It is true that a great many novel ideas, some of them surprising, perhaps even startling, emerge from the development of the consequences of this one basic innovation, but this is simply a result of the fact that this one new concept is introduced at the very base of the theoretical structure and it therefore has some kind of an effect on almost every part of that structure. In recognition of this major role which the reciprocal postulate plays in the system as a whole, this system will be designated as the Reciprocal System for the purpose of convenient reference in the subsequent pages. The word “system” is used rather than “theory” because the full development of the consequences of the postulates on which it is based leads to a whole network of physical relationships, each of which is comparable in scope to the gravitational theory which is the primary subject of the present discussion. This new development is not merely a theory but an interconnected system of theories.
It is evident that the reciprocal postulate necessitates the further assumption that space and time have the same dimensions, since quantities of different dimensions cannot stand in a reciprocal relation to each other. We can recognize three dimensions of space, and the simplest assumption that is consistent with both the reciprocal postulate and these observed properties of space is that both space and time are three-dimensional. Equally necessary in order to permit a reciprocal relationship of anything other than a purely formal character is the limitation of space and time to discrete units. Neither of these additional assumptions involves any great departure from current scientific thought. The possible existence of -dimensional time is a frequent subject of speculation in theoretical circles, and the continual extension of the property of discreteness to more and more physical phenomena, first to matter, then to electricity, then to radiant energy, then (somewhat tentatively) to magnetism, makes the further extension of the same concept to the basic entities, space and time, practically inevitable in the long run, irrespective of the requirements of this present work.
These three postulates constitute the definition of space-time as formulated on the basis of the considerations discussed in the preceding paragraphs. Together with the further assumption that space-time as thus defined is the sole constituent of the physical universe, they can be combined into one comprehensive postulate which may be expressed as follows:
First fundamental Postulate: The physical universe is composed entirely of one component, space-time, existing in three dimensions, in discrete units, and in two reciprocal forms, space and time.
In addition to this First Postulate which defines the physical nature of the universe, it will be necessary to make some further assumptions as to its mathematical behavior, in order that we may utilize mathematical processes in developing the consequences of the First Postulate. Until comparatively recently the validity of the mathematical relations which will be assumed in this work was generally considered axiomatic, but it has since been discovered that other more complex and unconventional relations are also theoretically possible, and although the existence of any physical realities corresponding to these unorthodox mathematics has never been definitely verified, these recent inventions are widely employed in present-day physical theory. In setting up a new theory, however, it is obviously advisable to return to the simpler and more manageable concepts of earlier days, unless and until this policy encounters obstacles. We therefore have the
Second Fundamental Postulate: The physical universe conforms to the relations of ordinary commutative mathematics, its magnitudes are absolute and its geometry is Euclidean.
It was demonstrated in the previous work that these postulates are sufficient in themselves, without the aid of any supplementary or subsidiary assumptions, to define a complete theoretical universe, but for present purposes we will confine the discussion to those aspects of the theoretical universe which are relevant to the subject of gravitation and we will limit the development of the consequences of the postulates to those items which are required for a complete understanding of the gravitational relations.
On examination of the Fundamental Postulates it is immediately apparent that they require a progression of space-time identical with that which was assumed as a basis for the development in Part Two. Let us consider some location A in space-time. When one more unit of time has elapsed this location has progressed to A + 1 in time. According to the First Postulate the one unit of time is equivalent to one unit of space, since the postulate specifies that space and time are reciprocal, hence this location also progresses to A + 1 in space.
It is also evident that the reciprocal postulate requires something beyond this equivalence of the single unit of time and the single unit of space. If this were the extent of the relationship we would postulate that time and space are equivalent; not that they are reciprocal. In order to make the relation reciprocal there must be certain conditions, under which associations of n units of one component exist, in which case the sense of the postulate is that these n units of the one component are equivalent to 1/n units of the other.
Next we will want to know how these associations originate; that is, how it is possible to modify the 1 to 1 ratio of space to time which exists in the general space-time progression. It is evident that such a modification cannot take place in space-time itself, as space and time are equal in any unit of space-time and are therefore equal in any number of units or any succession of units. The modification must be accomplished by some alteration in the factors affecting space or time individually, and in order to permit such an alteration there must be a difference between space (or time) individually and space (or time) as a component of space-time: the capacity in which it participates in the space-time progression. The only such difference for which there is any provision in the postulates is a difference in direction, and we therefore arrive at the conclusion that space-time as such is scalar and that direction is a property of space and time individually.
On this basis, if we replace an individual unit of one component by a multiple unit so that this multiple unit of the one component is associated with a single unit of the other, the direction of the progression of the multiple component must reverse at the end of each unit. Inasmuch as space-time is scalar, this reversal of space direction or time direction means nothing from a space-time standpoint and the regular rate of progression, one unit of space per unit of time, continues just as if there were no reversals. From the standpoint of space and time individually, the progression involves n units of one kind but only one of the other, the latter being traversed repeatedly in opposite directions. It is not necessary to assume any special mechanism for the reversal of direction. In order to meet the requirements of the First Postulate the multiple units must exist, and they can only exist by means of the directional reversals. It follows that these reversals are required by the postulate itself.
Because of the periodic reversal of direction a multiple unit replaces the normal unidirectional space-time progression with a progression which merely oscillates back and forth over the same path. But when the translatory motion in one dimension of space is eliminated, the oscillating unit is confined to a single space unit, and this unit of space then progresses in the normal manner in another dimension, carrying the oscillating unit with it. When viewed from the standpoint of a reference system that does not progress, the combination of an oscillating progression in one dimension and a unidirectional progression in a dimension perpendicular to that of the oscillation takes the form of a sine curve.
Obviously this feature of the theoretical universe defined by the Fundamental Postulates can be identified as radiation. Each oscillating unit is a photon, and the space-time ratio of the oscillation is the frequency of the radiation. Since space-time is scalar the actual spatial direction in which any photon will be emitted is indeterminate, and where a large number of photons originate at the same location the probability principles whose validity was assumed as a part of the Second Fundamental Postulate require that they be distributed equally in all directions. We find, then, that the theoretical universe defined by the postulates includes radiation consisting of photons traveling outward in all directions from various points of emission at a constant velocity of one unit of space per unit of time.
Another possible motion of the oscillating photon is a rotation. Let us consider next the factors involved in rotational motion of these units. Rotation differs from translation only in direction and this difference has no meaning from a space-time standpoint since space-time is scalar. Rotation at unit velocity is therefore indistinguishable from the normal space-time progression: that is, from the physical standpoint it is essentially the equivalent of no rotation at all. In order to produce any physical effects there must be what we will call a displacement: a deviation from unity. The deviation is necessarily upward, as fractional units do not exist, and the magnitude of any rotational motion of the photons is therefore greater than that of the space-time progression.
A second necessary characteristic of the rotational motion of the photons is that its direction must be opposite to that of the space-time progression, because any added displacement in the positive direction would result in a directional reversal and would produce a vibration rather than a rotation, as previously explained. This means that when the photon acquires a rotation it travels back along the line of the space-time progression, and since this retrograde motion is greater than that of progression (at unit distance) these rotating units are reversing the pattern of free space-time and are moving inward toward each other, either in space or in time, depending on the direction of the displacement.
For present purposes we will consider only those photons which are moving inward in space. Like the photons that are moving transitionally, the rotating photons of this type which exist in the theoretical universe defined by the Fundamental Postulates are readily correlated with observed physical entities. With the exception of a few that are dimensionally incomplete, they can be identified as atoms. Collectively the atoms constitute matter, the inward motion resulting from the rotational velocity is gravitation, and the incomplete atoms are sub-atomic particles.
At this point, then, it is clear that the two gravitational assumptions of Part Two are necessary and direct consequences of the two Fundamental Postulates; that is, the postulates lead directly to a progression of space-time and to an inherent motion of the atoms of matter in the direction opposite to the progression. All of the conclusions and relations derived from the gravitational assumptions in Part Two can therefore be incorporated en bloc into the theoretical system that is here developed from the Fundamental Postulates.
X
A very significant point about the theory outlined in the foregoing paragraphs is that the same feature of the theory, which leads to the existence of matter—rotation of the oscillating photons in the direction opposite to the space-time progression—also, causes matter to gravitate. This is, of course, a major step toward simplification of the basic physical relationships. It brings within the scope of one general theory two important items, which have hitherto required completely separate treatment. But this is by no means the full extent of the unification of the theoretical structure that has been accomplished. The developments in Part Two, which are also part of the new theoretical structure, since the assumptions of Part Two have now been shown to be necessary consequences of the Fundamental Postulates of the Reciprocal System, go on to derive from the same initial premises the major characteristics of gravitation, the instantaneous action, the absence of a medium and the impossibility of modification, and in addition they explain the principal deviations from what we may consider the “normal” pattern of gravitational action in two of the three regions in which such deviations occur. The somewhat abbreviated view of the situation given by the two gravitational assumptions of Part Two was not capable of explaining the deviations in the third of these regions, the region of atomic and molecular interaction, but a more complete development of the consequences of the Fundamental Postulates brings the relationships in this region within the scope of the gravitational theory.
Ordinarily the effect of the space-time progression is to move physical objects farther apart. Any two objects which are initially separated by x units of space-time will be separated by x + n units of space after n additional units of time have elapsed, as each unit of time is equivalent to a unit of space. However, if there is a space-time displacement of such a nature that the two objects are initially separated by x units of time in association with one unit of space (that is, by the equivalent of less than one unit of space) the result is quite different. In this case the progression takes place entirely within one unit of space and consequently space remains constant at one unit while time is free and progresses in the normal manner. In view of the reciprocal relation between space and time, the increase in time due to the unilateral progression is equivalent to a decrease in space, hence the effect of the progression on two objects initially separated by the equivalent of less than one unit of space is to decrease the equivalent space separation.
At first glance it appears inconsistent for the same space-time progression to move objects farther apart in one region and to move them closer together in another region. As emphasized in the previous publication, however, the seeming inconsistency is due to the use of the wrong datum in evaluating the situation. Because of the equivalence of the unit of space and the unit of time, the initial point of all physical activity is at unity, not at the mathematical zero. When we recognize this fact, the apparent inconsistency disappears. Now the progression always proceeds in the same natural direction: away from unity. Above unit distance, away from unity is outward; below unit distance it is inward.
Inasmuch as gravitation, by reason of its inherent nature, always acts in the direction opposite to that of the progression, a similar reversal occurs in the gravitational direction. Above unit distance, the gravitational motion is inward toward unity. Below unit distance it acts in the same natural direction, toward unity, but in this case toward unity is outward. Gravitation therefore exerts a force of attraction between two masses which are initially more than one space unit apart, but it exerts a force of repulsion between two masses which are initially less than the equivalent of one space unit apart.
With the benefit of this information, the nature of the inter-atomic force equilibrium now becomes clear. In the region outside unit distance there can be no equilibrium, as any motion resulting from an unbalanced force accentuates the unbalance. If the inward-directed gravitational force exceeds all outward-directed forces, for example, an inward movement takes place, which strengthens the already dominant gravitational force. In the region inside unit distance, on the other hand, any movement due to an unbalanced force reduces the unbalance and tends toward equilibrium. Here an excess gravitational force causes an outward movement, which weakens that force, and ultimately reduces it to equality with the constant force of the space-time progression, whereupon the motion ceases and the two objects take up equilibrium positions.
This explanation accounts for the existence of cohesion in solids and liquids and thus extends the application of gravitational theory to another major physical field for which a completely separate theoretical structure has hitherto been necessary. With this addition, the scope of the theory now includes the entire range of space intervals from the shortest interatomic distance to the separation between the most distant galaxies.
Throughout this entire immense region, the concept of a progression of space-time outward from unity provides the additional effect of a general nature, which is necessary in order to account for various phenomena that have hitherto resisted explanation. Physicists are understandably very reluctant to accept any such idea. It is quite distasteful to be compelled to admit that an unrecognized force of general applicability can still exist after the many centuries that they have devoted to intensive study of physical relations, and consequently they are strongly inclined to close their eyes to the fact that many existing situations are wholly inexplicable unless such a force is effective. But occasionally an admission is encountered in the literature. Gold and Hoyle, for example, tell us candidly, “Attempts to explain both the expansion of the universe and the condensation of galaxies must be very largely contradictory so long as gravitation is the only force field under consideration. For if the expansive kinetic energy of matter is adequate to give universal expansion against the gravitational field it is adequate to prevent local condensation under gravity, and vice versa. That is why, essentially, the formation of galaxies is passed over with little comment fin most systems of cosmology.40
The analogous problem of the globular clusters is “passed over” with even less comment. Examination of one after another of the available textbooks and dissertations on astronomy gives us no indication that there is any difficulty in accounting for the existence of these numerous and conspicuous objects. But if we search diligently through the astronomical journals we will find a few papers in which attempts have been made to analyze this problem, and almost invariably these papers begin with an admission such as the following from E. Finlay-Freundlich: “All attempts to explain the existence of isolated globular star clusters in the vicinity of the galaxy have hitherto failed.”41
Here again the difficulty arises from the fact that at least two forces are required in order to explain the existing situation, whereas the astronomers have only one force to work with. “Their structure must be determined solely by the gravitational field set up by the stars which constitute such a cluster,” says Freundlich, and he goes on to admit that on this basis, “The main problem presented by the globular star clusters is their very existence as finite systems…” In view of the absence of any evidence of rapid rotation, the only theory which the astronomers have been able to produce is that the behavior of the stars in the cluster is analogous to that of the molecules in a gas. “But the analogy is useless,” says R. v. d. R. Woolley, the Astronomer Royal, “unless collisions among the stars are sufficient to set up equipartition of energy, and not very valuable unless the mean free path for stellar encounters is small compared with the dimensions of the stellar aggregation considered. Calculation shows that the mean free path is probably large compared with the effective diameter of a cluster, so that in clusters the analogy with a gas is an idea that cannot be pushed very far.”42
All that we actually know about these clusters indicates that they are very stable structures and have probably existed in approximately their present forms for billions of years. This implies that they are in a state of equilibrium: a condition that existing theory cannot explain. Both Woolley and Freundlich concede that an isothermal equilibrium similar to that, which would be the final result in a gaseous system, would involve dispersion of the cluster. “The isothermal gas sphere’ is not a finite object,” Wooliey admits. Those astronomers who attempt to approach this problem are thus forced either to assume that the clusters are not in equilibrium. In the face of the observational evidence indicating that they are among the most stable and permanent of all astronomical objects, or else to modify the gas relations in an arbitrary and ad hoc manner, which destroys the cogency of the argument in favor of using the gas analogy.
Resort to such tactics is not necessary in the theoretical universe of the Reciprocal System, as this system provides the additional force that is necessary for equilibrium. Here each individual star (or multiple star system) is outside the gravitational limits of its neighbors and hence is moving away from them because of the space-time progression. At the same time, however, the gravitational effect of the cluster as a whole is pulling the individual stars in toward the center of the cluster. The net effect is equilibrium between these opposing motions (or forces).
When we turn to the inter-atomic situation, we find essentially the same thing. Here again the gravitational force and the postulated electrical force of attraction between the atoms are not sufficient to account for the equilibrium that actually exists, but the complete inadequacy of the currently accepted theories in this particular respect is simply ignored by all but a very few of the physicists. One of the few authors that has recognized and conceded the true nature of this problem is Karl Darrow, who examined the whole situation in 1942 in an article entitled Forces and Atoms.43 Darrow points out that both gravitation and the electrical force of cohesion (the existence of which he assumes, in accordance with current theory) are forces of attraction, and in order to produce an equilibrium there must be a third force: an “antagonist” to the attractive forces. “This essential and powerful force has no name of its own,” Darrow explains, “This is because it is usually described in words not conveying directly the notion of force.” By this means the physicist “manages to avoid the question.”
Darrow concludes his discussion of the problem with the comment, “This combination of a short-range attraction with a repulsion still shorter in range cries out for explanation. Could one but somehow reduce it all to inverse-square forces, one would be more contented.” This comment is particularly apropos at the moment, since what the Reciprocal System has accomplished is essentially what Darrow envisions: a reduction of the whole problem to equilibrium between an inverse-square force and a force of constant magnitude. In this system the constant space-time progression provides the inward force that is responsible for cohesion, while the gravitational force, reversed at the unit level, is the “antagonist” that accounts for the equilibrium.
The validity of this definition of the inter-atomic force system can be verified by an examination of the response of the system to external forces impressed upon it; that is, by a study of solid and liquid compressibility’s. A comprehensive study of this kind has been carried out in connection with the investigation on which this present work is based, and it is planned to include a summary of the results in a new and more complete edition of The Structure of the Physical Universe to be published in the near future. This data will show that the theoretical compressions derived from the equations of the Reciprocal System are in agreement with the measured values, within the probable experimental error, over the entire range of the experimental work, up to 100,000 atm.. static pressure and to several million atmospheres by the recently developed shock wave techniques.
XI
In our ordinary experience space and time appear to be altogether different in character. Space is the kind of a phenomenon that we intuitively feel that we can understand: a well-behaved entity with a comfortable sort of permanence that makes observation and measurement relatively simple. It is true that there are some basic philosophical questions concerning its ultimate nature that have been controversial issues ever since man first began to speculate about such subjects, but nevertheless space can be broadly classified as one of the more familiar features of our physical universe.
On the other hand, time has always been mysterious and elusive. It undoubtedly exists; there is certainly something that distinguishes the present from the past and from the future, and there is certainly some physical meaning attached to the symbol t that enters into so many of the mathematical expressions that we; use for the purpose of expressing physical relationships. But when we attempt to be more specific and to develop a more tangible concept to replace these rather hazy ideas, we encounter some extraordinary difficulties. We have not even been able to devise any direct measurement of time; the best we can do is to select some type of periodic motion and to assume that successive coincidences of identifiable spatial points connected with this motion distinguish intervals of time.
The most striking and prominent feature of time, as we observe it, is the continuous flow or progression. This is, in fact, just about all that we know about time. The most prominent feature of space is its extension in three dimensions. According to the Fundamental Postulates of the Reciprocal System, however, space and time are absolutely symmetrical and all of the properties now observed in either space or time individually are actually applicable to both. On the basis of this new viewpoint the great dissimilarity in the observed characteristics of the two entities is not due to any real difference between the two, but is a result of the gravitational motion of matter in the direction opposite to that of the space-time progression. This oppositely directed motion in space cancels the effect of the space progression in the local region and the results of the progression are visible only at the extreme range of our giant telescopes. The existence of this phenomenon has therefore remained unrecognized.
In our observations of time we recognize the progression but not the three-dimensional extension. A modification of the normal space-time ratio by substitution of an association of units for a single unit of one of the components produces a motion either in space or in time, but not in both. The inherent motion of matter is in space (because it is the units whose motion is in space that we call matter) and so far as matter is concerned, the progression of time continues as in free space. Since the velocity of the progression is so high, 186,000 miles per second, the differences in time location comparable to the differences, which we observe in spatial location, are, in most instances, relatively minor, and they are so over-shadowed by the progression that their true nature has not been perceived. Here again, there actually is a noticeable effect under extreme conditions (motion at very
Figure 2
high velocities) but it has not hitherto been realized that this discrepancy is chargeable to a misconception of the properties of time.
As an aid in visualizing this situation, let us consider the motion of a distant galaxy. In the constellation Hydra there is a faint galaxy which, according to the red shift in its spectrum, is receding from us at a velocity of over 35,000 miles per second, one-fifth of the velocity of light. So far as we are able to determine t his galaxy is moving directly away from our location and, except for the somewhat lower velocity, the recession of this and other distant galaxies has exactly the same characteristics as the progression of time: that is, it is a scalar motion which always proceeds in the same direction: linearly outward. According to the findings of this work, this galactic recession not only appears similar to the progression of time; it actually is the same kind of a phenomenon. It is the space equivalent of the time progression. The only reason why the galactic velocity is lower than that of light is that the Hydra galaxy, in spite of the enormous distance which separates it from our location in space, is still close enough to be subject to a small gravitational effect. At greater distances there undoubtedly are galaxies which are receding from us at practically the full velocity of light.
In Figure 2 the Hydra galaxy was at point A at time to. During a time interval t the recession carries it from point A to point B. The intervening distance AB is the space equivalent of a time interval resulting from the constant progression of time, and since we refer to the latter as clock time, we may utilize the same terminology and call the distance AB the clock space. From our far distant location, this movement from A to B in clock space is the only movement of the Hydra galaxy that we can distinguish, but we know from observation of less distant galaxies that these galactic aggregations also have random motions in space, and we can therefore deduce that the Hydra galaxy will not actually be found at point B when t units of clock time have elapsed; it will be found at some other point C. The random motions of the galaxies are not restricted to the dimension of the recession; that is, the distance BC, which represents the random motion during time t is not necessarily a prolongation of AB, but may have any direction in three-dimensional space. The total distance traveled by the Hydra galaxy during time t is therefore the vector resultant of the clock distance AB and the distance BC due to the random motion, the latter being a distance in the familiar three-dimensional space of our everyday experience. In order to distinguish this kind of space from the clock space, we may call it coordinate space, since we usually define it by means of some coordinate system.
Summarizing the foregoing, we may say that the total space traversed by the Hydra galaxy in any specified interval of clock time consists of two separate components: the clock space, which is the distance covered by the galactic recession (the progression of space) and the coordinate space, which is the distance covered in three-dimensional space by the random motion of the galaxy. Inasmuch as there is no reason to believe that this particular galaxy is exceptional or privileged in this respect, we may apply the same conclusion to all galaxies, including our own. In the case of the far distant galaxies, such as Hydra, we can detect only the motion in clock space; in observation of our own or other galaxies of our local group the motion in clock space is masked by the gravitational motion, and we see only the motion in coordinate space. But it is clear that these are merely observational deficiencies; the two separate components exist in all cases whether we can detect them or not.
In view of the reciprocal relation between space and time it is evident that exactly the same conclusions apply to time. The total time interval in any physical situation includes not only the clock time due to the constant time progression, a one-dimensional movement analogous to the galactic recession, but also another component, the coordinate time, due to random movement in three-dimensional time. Normally we detect only the clock time because the coordinate time component is negligible (relatively), but under extreme conditions, such as very high velocities, the coordinate time may be quite significant. As in the analogous case of the receding galaxy, the actual point c in time occupied by an object at a particular stage of the progression is something other than the clock time b, and since many values of c may correspond to the same value of b, the true time interval cannot be expressed in terms of the clock system of reference (that is, in clock time) except in certain special cases, such as that in which b and c are practically coincident (which is true at low velocities) or where the local motion follows a pattern of a restricted type, such as uniform translational velocity.
This is the basic error in all previous theories of motion. All theories that have enjoyed any substantial degree of support have assumed a one-dimensional, one-valued time. “…we shall assume without examination… the unidirectional, one-valued, one-dimensional character of the time continuum,”44 says Tolman. But this is clock time, not the total time that actually enters into physical processes.
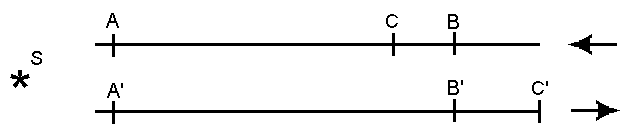
Figure 3
Newton’s Laws of Motion are based on the primitive concepts of space and time: a three-dimensional Euclidean space (coordinate space) and a one-dimensional time progressing uniformly and having the same value at all points in space at each stage of the progression (clock time). For two hundred years these laws met every test, with nothing more than minor discrepancies which were not regarded very seriously. Then in 1887 the Michelson-Morley experiment shattered the foundations of Newton’s structure. Figure 3, adapted from Tolman,45 shows the nature of the problem introduced by the results of this experiment. Let us assume that a ray of light from a distant source S passes from A to B and from A’ to B’ in two parallel systems. Then let us assume that the systems AB and APB’ are in motion in opposite directions as shown, and are in coincidence as the light ray passes A and A’. Because of the motions of the respective systems, point B will have moved to some point C closer to A by the time the light reaches it, whereas B’ will have moved to some more distant point C’. Yet if the results of the Michelson-Morley experiment are to be believed, the velocity of the incoming ray at C is identical with the velocity of the incoming ray at C’; that is, the velocity of light is independent of the reference system. As Tolman expresses it, the time required for the light to pass from A to C measures the same, as the time required to pass from A ’to C’: a conclusion which, as he says, is “in direct opposition to the requirements of so-called common sense.”45
This comment by Tolman shows very clearly just where and how the thinking of the scientific profession was diverted into the wrong channels. In reality the Michelson-Morley experiment does not indicate that the time ac is equivalent to the time a’c’; it merely shows that the velocity of light over the path AC is the same as the velocity over the path A’C’. The further conclusion that the two times are equivalent is not an experimental finding; it is an interpretation of the experimental findings in the light of the currently popular assumption as to the nature of time.
It is evident from the points brought out in the preceding paragraphs that we do not need to abandon common sense to explain this situation; all that we need to do is to get a broader view of time which will encompass all of its properties, not just the progression. The correct explanation of Tolman’s diagram is that points A and B are not only separated by the coordinate distance AB; they are also separated by an equal amount of coordinate time, since each unit of space, according to the Fundamental Postulates, is equivalent to a unit of time. The movement of point B to location C not only reduces the space separation between the original location of A and the new location of B by the amount of coordinate space BC, but also reduces the time separation by bc, the same amount of coordinate time. If the velocity of the system AB is relatively low, as most velocities are in the world of our everyday experience, the time bc is negligible in comparison with the time of the progression, but if the velocity is great enough to make it necessary to take the distance BC into account, then we must also take the equivalent time bc into account. The Newtonian concept of time in conjunction with the results of the Michelson-Morley experiment leads to the relation AC/t = A’C’/t, which is absurd, as Tolman tells us. But when we realize that the motion which reduces the distance from AB to AC also reduces the time from ab to ac, the relation of the velocities in the two systems becomes AC/ac = A’C’/a’c’ which is fully in accord with both common sense and common mathematics.
The extreme condition is illustrated in Figure 4. Here two light photons leave point O simultaneously and travel in opposite directions. Photon a moves one unit of space OA in one unit of time. Photon b moves one unit of space OB in one unit of time. (The system of space and time units is immaterial. Irrespective of the conventional units employed, we reduce them to the same proportionality by defining the velocity of light as unit velocity.) According to Newton, the relative velocity of the two photons is then 2/1 = 2, since the space separation at the end of one unit of time is AB, or two space units. But the experimental results show that the velocity of light is independent of the system of reference, and that the relative velocity is actually one unit, not two. Newton’s system therefore gives us the wrong answer.
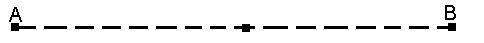
Figure 4
Einstein met the situation by abandoning the concept of absolute space and time magnitudes and accepting the hypothesis, originally advanced by Fitzgerald, that space contracts in the direction of motion. On this basis the distance AB no longer has the value 2, as it does in Newton’s system. The constant velocity of light is accepted as a fundamental property of nature, and it is assumed that the distance AB is automatically reduced to whatever value is necessary in order to make the quotient s/t equal to this constant velocity, generally represented by the symbol c or, as in the present discussion, defined as unit velocity. In the Einstein system the equation of motion for Figure 4 becomes s/1 = 1, where s is arbitrary, or more generally s/t = 1, where both s and t are arbitrary, as for some purposes, at least, it becomes necessary to assume a dilatation of time as well as a contraction of space.
Einstein’s concept of space as a purely relative magnitude, varying according to the location and velocity of the observer, is incompatible with the somewhat intuitive ideas synthesized from everyday experience and generally described by the term “common sense.” The scientists of the early twentieth century were therefore very reluctant to accept it, but Newton’s system, with its absolute time and space, had been invalidated by the experimental demonstration of the constant velocity of light, and since no plausible alternative was proposed (other than some variations of the Relativity Theory itself) this concept of a “rubber yardstick” won acceptance by default. A factor that contributed greatly to this acceptance was that the principal obstacle standing in its way, the prejudice against violation of common sense principles, was undermined by the fact that the experimental results appeared to be, as Tolman remarked in the statement previously quoted, “in direct opposition to the requirements of so-called common sense.” Obviously if the facts themselves are in conflict with common sense, it is no longer consistent to demand that theory stay within common sense boundaries.
With the benefit of the information that has been developed in this work, however, it is clear that Einstein’s drastic step in abandoning absolute space and time was neither necessary nor justifiable. Both Newton and Einstein failed to recognize that there are two components of physical time and both set up their theories on the assumption that we are dealing only with clock time. On this assumption the time required by photon a to travel from O to A is the same unit of time as the time required by photon b in traveling from O to B. But the unit of distance is separate and distance from the unit OA and since two separate units of distance are traversed by the photons, the equivalence of the individual units of space and time postulated in this work requires the corresponding units of time to be separate and distinct. In other words, when the photons are at points A and B respectively and are separated by two units of space they are also separated by two units of time. The equation of motion is then 2/2 = 1, which is completely in accord with the results of the experiments.
It is now apparent that Tolman misunderstood the nature of the message, which the Michelson-Morley experiment was trying to convey (as did Tolman’s colleagues, including Einstein. Tolman’s work is being used for purposes of illustration merely because it is a particularly clear presentation of the currently accepted viewpoint). The results of this experiment do not, as Tolman asserts, require us to contradict the “requirements of common sense” and accept the time elapsed between A’ and C’ as being the same as that between A and C. What these results actually tell us, if we read their message correctly, is that the concept of time which leads to this absurd conclusion, the concept that has hitherto been universally accepted, is wrong.
This orthodox concept of time is based on a narrow view which recognizes only one of its aspects, the progression, whereas the preceding pages have shown that a theoretical analysis of the situation, supported by observations of the motions of the distant galaxies and by the observed properties of radiation, leads to the conclusion that time also possesses all of the attributes that are recognized in space. When it is thus realized that space and time are completely symmetrical, it becomes apparent that all of the magnitudes applicable to time are commensurate with the corresponding magnitudes applicable to space. The individual locations are not necessarily coincident. In Figure 3, for example, the time locations a, b and c, which now correspond to space locations A, B and C respectively, may be changed to d, e and f as a result of the progression of time, but the new time separation de then corresponding to the space separation AB will still be equal to AB and also to de. This simplifies the problem of measurement of the time separation very materially, since we can readily measure the coordinate space separation between any two accessible objects, and this value, when expressed in appropriate units, is also the coordinate time separation between these objects.
Both the complexities and the limitations of Einstein’s Relativity Theory arise from the fact that he was unable to see the broad picture and attempted to describe all physical events in terms of clock time only. As indicated in the preceding discussion, a revision of the basic concepts to take all of the properties of space and time into account eliminates the necessity for any arbitrary manipulation either of the mathematical relationships or the physical magnitudes. Everything then falls into line easily and naturally without any kind of artificial maneuvering or any conflict with common sense.
XII
One of the most significant features of the Reciprocal System is that it is a purely theoretical construct. All of its elements are sharply and positively defined because they are derived from pure theory and have no empirical content (even though the theory itself was derived by inductive reasoning from empirical premises). This system is therefore completely untouched by most of the uncertainties and ambiguities that have troubled conscientious critics of previous theories. Bridgman points out; for example, that Relativity Theory is based in the first instance on the assumption of the existence of some kind of a physical framework defined by means of rigid measuring rods and clocks. But, as he says, there is no “very articulate analysis” of what is meant by “rigid,” and he continues, “The specification of what is meant by a clock is usually even less articulate, and has been felt to be a matter of much difficulty by a number of critics… in practice it almost appears as though the only criterion for a clock is whether it functions in the way that the equations demand that a clock function.”46
Similar considerations apply to all of the concepts entering into physical theory, and a recognition of this situation has led to the emergence of the “operational” point of view, the adherents of which contend that physical concepts should be defined solely in terms of the operations by which they will be detected and measured. This is, of course, impossible for such elementary concepts as those of clocks and measuring rods, but once these basic elements have been defined, the methods by which they are utilized in observing and measuring other more complex entities can be used as bases for the physical definition of those entities. Such reasoning, applied to the concept of simultaneity, played a major role in Einstein’s development of the Theory of Relativity and it has exerted a significant influence on modern physical theory as a whole.
Questions of this kind do not arise in the Reciprocal System. The universe developed from the Fundamental Postulates of this system is purely theoretical and any concept such as that of a clock can be specifically defined on a strictly theoretical basis. By means of the same structure of theory the kind of a physical entity that can qualify as a clock under this definition can also be specified unambiguously. Up to this point it is not necessary to take the actual physical world into consideration in any way, but once we have arrived at a conclusion which, for example, might be that any body in uniform rotational motion constitutes a clock, the next move is to examine the physical universe to determine whether or not we can identify any body in uniform rotational motion. If we can find such an entity, then we have a clock. In following this procedure we have actually used, on a rigidly correct theoretical basis, the practical criterion described by Bridgman; that is, we say that a rotating body is a clock because it functions in the way that a clock theoretically should function. If it functions exactly according to the theoretical requirements, then it is an accurate clock.
This is the same procedure that we apply to all physical phenomena when we utilize the Reciprocal System. We first determine what sort of thing should exist in the theoretical universe and then we look to see if we can find an entity in the observed physical universe, which conforms to the theoretical description. For instance, we do not put gravitation into our theoretical universe because we know that it exists in the real physical universe. We put nothing into the theoretical universe but the Fundamental Postulates, and gravitation is there only because its existence is a necessary and unavoidable consequence of those postulates. Similarly, the properties, which are attributed to gravitation in the theoretical universe, do not depend in any way on the properties that we find by observation of the physical phenomenon of gravitation; these theoretical properties are also necessary consequences of the postulates.
Of course, the theoretical development gives us no names; it simply gives us a description of the various components of the theoretical universe and, unless we wish to coin some new names for the theoretical entities, which would be confusing and would serve no useful purpose, we have to locate the physical entity corresponding to the theoretical description in each case before we arrive at a name. The theory merely tells us, for example, that a certain phenomenon exists in which oscillating units, with various frequencies of oscillation, originate at different points in space and travel away from these points in all directions at a constant velocity. When we turn to the actual physical universe, we find that a phenomenon with exactly the same characteristics also exists there. We are then justified in concluding that this physical phenomenon, which we call radiation, is the physical equivalent of the theoretical phenomenon deduced from the Fundamental Postulates, and we therefore apply the name “radiation” to both.
When we have thus identified a physical entity with its theoretical equivalent, we can carry over into the physical field all of the properties and relationships applying to the corresponding theoretical entity, irrespective of whether or not the available observational data are adequate for a physical verification of all of the theoretical conclusions. In the case of gravitation, for instance, we can confidently assert that the gravitational effect is instantaneous, because it is necessarily instantaneous in the theoretical universe, even though this point is contested by most theoretical physicists, including Einstein, not because of any evidence to the contrary, but because it is inconsistent with their theories.
In asserting that the gravitational effect is instantaneous, the Reciprocal System does not arrive at any new conclusion; it merely takes a position on one side of a long-standing controversy, but we are equally justified in going still farther and applying to the physical universe other features of the theoretical universe defined by this system which are completely new and in some cases totally foreign to current thinking. The reversal of direction of gravitation at unit distance is an item of this kind. Here is something that has never even been suspected, and which does not fit in very well with orthodox lines of thought. It will consequently meet with much resistance, but there is no logical or factual basis on which it can be rejected, since it is not inconsistent with any known fact, while on the affirmative side there is the very powerful argument that the explanation of the cohesion of solids provided by this gravitational reversal enables the inter-atomic distances in solids, and the changes in these distances under pressure, to be accurately calculated from pure theory.
This is the kind of a place where the immense advantage of a theory that is both complete and correct makes itself manifest. All that we know about solid and liquid cohesion form observation and experiment is that there must be two forces involved in the inter-atomic equilibrium: a force of attraction that holds the atoms together in the two condensed states, and a force of repulsion that limits the closeness of approach. (This is equally true whether or not the atoms are in contact. If they are in contact there must still be a force within the atom resisting deformation.) It does not appear likely that any more detailed information about these forces will be obtained from observation without some fairly specific clue as to what to look for, and in order to find such a clue we must first formulate a theory of the inter-atomic force system.
Heretofore there has been no available source of such a theory other than pure invention, and it is painfully obvious that the theorists’ inventive capacity has been completely inadequate for this task. There is no doubt as to the existence of the repulsive force. If we apply external pressure to a solid or liquid aggregate, the atoms move closer together, and as they do so the resistance to the compression increases as a function of the displacement from the original equilibrium positions—up to the experimental limits of several million atmospheres, at least—but, as Darrow pointed out in the article previously quoted,93 the physicists have not even attempted to construct a theory which would account for anything other than the for ce of attraction. They have simply “managed to avoid the question” of the “essential and powerful force” that plays the role of an “antagonist” to the attractive force. A hypothesis which makes no attempt to account for more than one of the two participants in an equilibrium certainly cannot claim to be an explanation of the phenomenon in question, and present-day science therefore has nothing that can be legitimately called a theory of the inter-atomic forces.
In such a case, where the information obtainable from direct observation of the phenomenon itself is too meager to point the way to an adequate theory, there is an alternative possibility: the theoretical principles governing the situation may be deduced from relationships previously established in collateral fields. This is where the necessity for a complete and correct theory arises. An incomplete and approximate theory may be of considerable value in the field to which it is directly applicable, but it seldom accomplishes anything of any consequence outside of that field. Even the gravitational theory based on the two assumptions of Part Two, which is actually correct, as far as it goes gives us no help at all with the inter-atomic problem. But when these two gravitational assumptions are traced back to their source in the Fundamental Postulates of the Reciprocal System, and the further consequences of these postulates are developed in detail, we can obtain a complete and comprehensive picture of the inter-atomic forces in all of their manifestations and the acute questions concerning the nature of solid and liquid cohesion, including the identification of both the attractive and the repulsive forces, are answered as a part of the clarification of the general situation.
In the present state of physical knowledge it is not at all likely that a hypothesis such as that of a “natural” direction of gravitation—always toward unity—would ever be formulated ad hoc; there is nothing elsewhere in the physical universe to suggest anything of this kind. On the other hand, when it develops that this constant direction toward unity, which involves a reversal of the gravitational force at unit distance, is a necessary and unavoidable consequence of principles firmly established in other fields, and on applying this conclusion to the cohesion problem we find that it accounts for the observed facts both qualitatively and quantitatively, it is in order to conclude that this hypothesis is a correct statement of the true physical situation. Throughout the many fields, which have thus far been covered in developing the details of the theoretical universe of the Reciprocal System, similar cases have been encountered frequently. In each of these instances the solution of a difficult problem of long standing was found to require some conceptual innovation or reversal of a habitual trend of thinking which by itself was almost inconceivable, yet proved to be fully in accord with the known facts when a careful and critical examination was finally undertaken because the need for such an innovation was established in the course of the development of the Reciprocal System.