XVII
Although the description of the new theory of gravitation given in Part Three is essentially complete as it stands, it may be helpful to show how the new concepts of the Reciprocal System affect some of the specific issues that have received special attention in previous studies of the subject.
The basic position occupied by the concept of a clock has already been mentioned. Since we have no means of making a direct measurement of time, we find it necessary to select some physical object with a uniform periodic motion and to utilize successive coincidences of identifiable spatial locations connected with this motion to distinguish intervals of time. Such an object then constitutes a clock. A very important point that has not been recognized heretofore, but which is brought out clearly in the previous theoretical development, is that a clock does not measure the total time interval; it measures only the time progression. Referring back to the discussion of the motion of the Hydra galaxy in Part Three, if we utilize a device which measures only the change in position due to the recession and ignores the random motion, we have the space equivalent of the clock which we use for the measurement of time. Where the random velocity is low, the inaccuracy thus introduced is negligible, but if this velocity is high and the changes in position due to the random motion are appreciable in comparison with the movement due to the recession, the measurement obtained by means of this “space clock” is seriously in error. So it is with clock time. As long as velocities are low the difference between clock time and total time is inappreciable, but at high velocities there is a serious discrepancy.
One of the major sources of confusion in the application of the Relativity Theory is the conclusion, which follows logically from Einstein’s basic assumptions (including the items that were simply taken for granted, “without examination” as Tolman puts it, as well as those that were expressly stated), that the clocks in a moving system run at a different rate from those in a stationary system, if both rates are measured in the same system of reference. When we recognize the true nature of a clock, which is a device that measures the time progression only, it is obvious that all accurate clocks are equivalent irrespective of location or system of reference, just as the rate of recession of a galaxy is the same for all points in the galaxy. But Einstein saw that the total time in a moving system differs from that in a stationary system, and not realizing that there are two components included in this total time, he thought that he was dealing with clock time only and therefore deduced erroneously that the clock time varies.
This is the origin of many of the so-called “paradoxes” of Relativity including the famous Twin Paradox, in which the conclusions drawn from a straightforward application of the Relativity principles are so outrageous that many of the staunch supporters of the theory are reluctant to accept them, and they have occasioned a great deal of controversy within the ranks of the relativists themselves. In the usual statement of this paradox it is assumed that one of the twins remains on earth, whereas the other embarks on a journey into the far reaches of the Galaxy, traveling at a velocity approaching that of light. According to the Relativity Theory, the clocks by which the fast-moving twin lives are slowed down to a very low rate, hence he returns from his journey in what to him was a rather short time, and he comes back still a young man, while his twin brother has been subject to the faster-moving clocks on earth and has grown old in the meantime.
Such fantastic conclusions are, of course, incompatible with the principles of the Reciprocal System. In this system the operation of clocks, the aging process, and all other such time-connected mechanisms in which no appreciable differences in coordinate time are involved, are determined by the relationships of the various factors as they exist in the local environment, and whether or not that environment is in motion, relatively or absolutely, is entirely irrelevant. Any change in position in time other than that resulting from the ever-present progression and registered on all clocks, affects only those relationships in which a significant difference in coordinate time is involved.
A somewhat modified statement of the initial premises arrives at what is called the Clock Paradox. Here it is assumed that clock B is accelerated relative to clock A and that subsequently, after a period of time at a constant relative velocity, the acceleration is reversed and the clocks return to their initial locations. According to the principles of Special Relativity clock B. the moving clock, has been running more slowly than clock A, the stationary clock, and hence the time interval registered by B is less than that registered by A. But Special Relativity also tells us that we cannot distinguish between motion of clock B relative to clock A and motion of clock A relative to clock B. Thus it is equally correct to say that A is the moving clock and B is the stationary clock, in which case the time interval registered by clock A is less than that registered by clock B. Each clock therefore registers both more and less than the other: definitely a paradoxical situation.
Tolman explains, “The apparent paradox is, however, readily solved with the help of the general theory of relativity, if we do not neglect the actual lack of symmetry between the treatment given to the clock A which was at no time subjected to any force, and that given to the clock B which was subjected to the successive forces F1, F2, and F3 when the relative motion of the clocks was changed,”73 and he goes on to develop his solution with several pages of the usual complex Relativity mathematics. “The solution thus provided,” he says, “gives a specially illuminating example of the justification for regarding all kinds of motion as relative…”
The alleged solution of the paradox does more than this; it provides us with a “specially illuminating example” of the way in which the originator of the Relativity Theory and his disciples pass hastily over the weak points in their initial assumptions and concentrate their c efforts on building up an invulnerable mathematical structure, apparently oblivious to the fact that the right answers cannot be obtained from the wrong premises, regardless of the power of the mathematical techniques. Let us go back and take a good look at these initial assumptions Tolman begins with the clocks in coincidence and subjects clock B to a temporary force which produces an acceleration relative to clock A. Then follows an extended period of time during which clock B has a velocity u relative to clock A. The Relativity Theory insists that this velocity u is purely relative: that there is no such thing as absolute velocity. On this basis, therefore, we cannot say that one clock is moving and the other stationary; irrespective of how the present situation originated each clock is moving relative to the other and we cannot attribute any motion to clock B that cannot be attributed equally legitimately to clock A.
Furthermore, if the end result is a purely relative motion as the theory contends, then the acceleration that produced the motion must be purely relative, since an absolute acceleration would not produce a purely relative motion. It then follows that the force must also be relative, in order to produce a relative acceleration. Tolman definitely states that the “successive forces F1, F2 and F3” cause a change in the “relative motion of the clocks.” If this orthodox relativistic view of the situation is correct, then we cannot attribute the change in motion to clock B any more than to clock A, and this in turn bars us from assuming that the forces are applied specifically to clock B. Tolman’s assumption as to the application of the forces contradicts the basic principles of the theory on which he bases his analysis, and hence the entire “solution” is invalid, irrespective of the elegance of the mathematical treatment.
If we hew to the line and apply the Relativity principles consistently throughout the argument concerning the Clock Paradox, the end result is an absurdity. Strictly according to these principles, it is not possible to apply a force specifically to a particular mass. Force is defined, by Einstein as well as by Newton, by means of the equation F = ma and just as acceleration must be relative to produce relative motion, force must also be relative to produce relative acceleration. This relativity of force does not make much sense, if we judge the idea according to our normal standards, but it is a necessary consequence of the Relativity Theory, and if it does not make sense, this simply means that the Relativity Theory itself does not make sense. Those who claim to have resolved the paradox and circumvented the reductio ad absurdum have simply forsaken Relativity and reverted to the “absolute” system at one point or another in their development.
Tolman does not specifically admit that he is violating Relativity principles and giving clock B an absolute acceleration, but Moller is more candid and concedes that the acceleration of clock B is “relative to the fixed stars” 74 an expression which is merely a euphemism for absolute acceleration. The fixed stars are taken as representing in an approximate way the general background of the universe, and motion relative to these stars is motion relative to the universe as a whole. Since we have only one universe, so far as we know, there is no meaningful distinction between this kind of motion and “absolute” motion. As Eddington puts it, “motion with respect to… any universally significant flame would be called absolute.”75 Thus both Tolman and Moller find it necessary, in order to resolve the Clock Paradox which results from the application of Relativity Theory, to assume the existence of absolute motion: a concept whose validity is specifically denied by Relativity Theory.
The truth of the matter is that the adherents of the Relativity Theory have allowed themselves to be so carried away by their enthusiasm for a theory which gives them plausible answers to some of the perplexing questions concerning the laws of motion that they have accepted the basic assertions of the theory without giving them the kind of critical scrutiny that should properly be applied to innovations in science. The assertion that it is impossible to distinguish between motion of A relative to B and motion of B relative to A is a case in point. Eddington cites the example of a train passing a station at 60 miles per hour. “Since velocity is relative,” he contends, “it does not matter whether we say that the train is moving at 60 miles an hour past the station or the station is moving at 60 miles an hour past the train.”76 Then he spends the next three pages trying to “explain away” (using his own expression previously quoted) the fact that if the relative motion is suddenly changed—by an accident, for instance—the passengers in the train are the ones that suffer injuries, not the occupants of the station.
But this situation cannot be explained away, and Eddington’s attempt gets nowhere. The motion of the train past the station is something of a totally different character than the motion of the station past the train, however strongly Eddington and his colleagues, past and present, may assert the contrary. We know that the accident causes a change in the relative velocity of the station with respect to the train, but we also know that this accident does not change the absolute velocity of the station, because we have a system of essentially constant absolute velocity, the surface of the earth, that we can use for reference. On the other hand, we know from similar considerations that the train undergoes an alteration of both its absolute velocity and its relative velocity with respect to the station. This demonstrates that a change in relative velocity only produces no physical effects, whereas a change in relative velocity arid absolute velocity does. It is clear from this that only absolute velocity has any physical significance; the relativists’ contentions that “There is no meaning in absolute velocity” and “There is no meaning in absolute acceleration”77 are one hundred percent wrong.
The proponents of the Relativity Theory have simply taken advantage of the prevailing strong desire for some kind of an explanation of the experimentally verified deviations from Newton’s Laws of Motion and have persuaded the scientific community to accept the extraordinary reasoning that since uniform absolute velocity cannot be detected by a particular kind of an experiment specified by the relativists themselves, absolute velocity does not exist, no matter how many other ways there may be of detecting it. Even the well-known willingness of scientists to go to almost any lengths to avoid admitting ignorance is hardly enough to explain their uncritical acceptance of this argument based entirely on inability to detect absolute translational motion by methods available within an isolated system, when it is clear that absolute motion (that is, motion relative to the universe in general) can be detected by means of observations extending outside that system, and that absolute acceleration, which implies the existence of absolute motion, can be detected not only by such external observations but by evidence obtainable within the isolated system as well.
This technique of dealing only with artificially simplified systems, which is standard practice in explanations and discussions of Relativity, arrives at conclusions which are, for all practical purposes, meaningless. Conclusions with respect to “isolated systems” have no meaning in relation to actual physical systems, all of which are constituent parts of the physical universe as a whole. Just as soon as we place the isolated system in its proper place in the universe, it becomes obvious that we do have an absolute system of reference defined with the aid of the fixed stars. As Moller admits, “Experience shows that the fixed stars as a whole may be regarded as approximately at rest relative to the ‘absolute space’…”78 Similarly Eddington’s futile efforts to “explain away” the effects of a sudden deceleration of his hypothetical train are seen in their true light when we consider the train-station system in its actual setting rather than in a fictitious Isolation.
An extreme example of this sort of thing is provided by the attempts that have been made to portray rotational motion as purely relative. Tolman considers the case of a rotating platform and concludes that “…we can with equal success treat the platform or the remainder of the universe as subject to the rotation.”79 When we consider the fantastic velocities that the distant sectors of the universe would have to possess in order to account for even a modest rate of revolution of the platform, this statement of the relativist position is nothing short of outrageous; when we go a step farther and ask how the rotation of the “remainder of the universe” could accommodate itself to numerous relative rotations at different velocities and around different centers of rotation, it is evident that the whole concept is utter nonsense.
The paradoxes of Relativity are merely consequences of the fact that the entire theory is constructed on a false conceptual foundation: one which attempts to compensate for a basic error in its definition of the nature of time by the introduction of a fictitious variability in space and time magnitudes. Such paradoxes cannot be resolved on any logical basis; they are inherent in the structure of the theory itself.
XVIII
Closely connected with the concept of the clock is that of simultaneity. This is another of those expressions whose meaning seems obvious in ordinary usage, yet turns out to be quite elusive when we attempt to be more specific. In large measure this difficulty stems from the very hazy nature of the existing concepts of time itself. As Tolman puts it, “To attempt a definite statement as to the meaning of so fundamental and underlying a notion as that of time is a task from which even philosophy may shrink.”80 We can hardly expect to be able to formulate a clear definition of what we mean by the expression “the same time” while we have only a vague idea as to what we mean by the word “time,” and the first objective of the present work was to accomplish a clarification of the basic nature of this phenomenon. Even when its nature and properties are definitely and positively spelled out, as they are in the Reciprocal System, however, we are still laboring under a handicap because we are not accustomed to thinking of time in these terms. It may therefore be helpful to take advantage of our greater familiarity with space and to define just what we mean by “the same place” before we attempt to consider the meaning of the analogous expression “the same time.”
As brought out in the discussion of basic physical principles in Part Three, any object which has no independent motion of its own, and which must therefore stay in the same place indefinitely unless it is acted upon by some outside agency, actually moves outward at the constant velocity of one unit of space per unit of time. From the natural viewpoint, therefore, “the same place” is a thing in motion. In common usage, however, the term “the same place” means the same place with respect to some arbitrary reference system. For ordinary purposes the reference system is the earth; astronomers find it more convenient to use the sun, or in dealing with more distant regions, the Galaxy. In all cases the reference system that is selected is one that does not progress in space (although it is usually in motion) and “the same place” as defined by such a reference system is the same relative location in coordinate space.
It is evident that “the same place” in clock space, the space of the progression, means the same point in the progression, and since the path of the progression can be identified in terms of the reference systems utilized for coordinate space, all points in a progressing system are in constant motion relative to our usual frames of reference. A distant galaxy which has no random motion does not remain at the same place relative to one of these conventional reference systems (our galaxy, for example); it occupies a specific place only momentarily and the progression then moves it along to another place. Our galaxy is similarly progressing outward away from the distant galaxies and from the overall standpoint, therefore, two events cannot occur at the same place unless they also occur at the same time.
On first consideration this statement seems to outrage common sense. Surely if I walk across the intersection of First and Main Streets today, I can return to the same place and do the same thing again tomorrow. But a little reflection will tell us that, even without the progression, First and Main Streets will not be at the same location in the universe tomorrow that it is today. Of course, this intersection does remain at the same place with respect to our usual system of reference, the surface of the earth, but if we look at the situation from a broader viewpoint we will realize that in the meantime the earth will have traveled more than 1½ million miles in its orbit around the sun; it will have accompanied the sun and its fellow planets over a distance of some 15 million miles on the long path around the center of the Galaxy; and it will have been carried an unknown distance by the movement of the Galaxy itself. The progression merely adds one more motion to the many others that exist. No, we cannot return to the same location in the universe tomorrow. Whatever we wish to do at that same place (as thus defined) can only be done at the same time.
So far as time is concerned, our reference system is analogous to a distant galaxy, as the progression of time continues unchecked in the material universe. In view of the symmetrical relation between space and time we may therefore invert the previous statement and say that two events cannot occur at the same time unless they occur at the same place. Events that take place at different locations cannot be simultaneous with reference to time in its totality.
It is possible, however, to define “the same time” in the same manner as we normally define “the same place” ; that is, with respect to a reference system which is stationary in one of the two components of time. We could, for instance, define the expression “the same time” as meaning the same point in coordinate time, just as the usual meaning of the expression “the same place” is the same point in coordinate space. But this would require a reference system stationary in coordinate time, and since we have no such system in the material universe, the time referred to a system of this kind would be meaningless to us. It is also possible to define “the same time” as the same clock time; that is, the same point in the progression, and this is a more practical alternative, as in so doing we are conforming to the meaning of simultaneity as the term is used in common parlance.
Once again let us turn to the galactic recession as an aid in visualizing the time relations. Figure 5 represents a galaxy that is receding at approximately the velocity of light in the direction shown. The entire galaxy recedes or progresses in space as a unit, hence the particular point in the progression which it occupies at any instant, the clock space applicable to the galaxy as a whole, can be identified by utilizing the position of any specified location within the galaxy as a reference point. Let us take the center of the galaxy for convenience. When this center is at point A, the clock space for the entire galaxy is XA, the distance between A and some previous location X
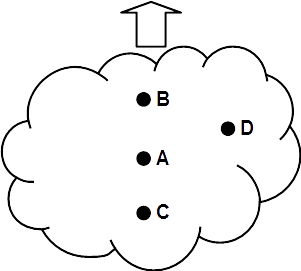
Figure 5
of the galactic center which will be taken as the origin of the coordinate system. At the same stage of the progression point B is at distance XB from the origin of the coordinates, but this does not mean that the clock space is any different at this location; the clock space is the distance which the galaxy has been moved by the progression during a certain interval of time, and since that distance is XA for one location within the galaxy, it is likewise XA for all other points in the galaxy. There is, however, a coordinate space AB intervening between A and B. hence the total distance from X to B. the position of point B in terms of the coordinates based on X, is XA plus AB, or XB. Similarly, the total distance between location C and the origin of the coordinates is XA minus AC, or XC. For a location such as D which is not collinear with A and X, it is necessary to convert the distance AD in three-dimensional coordinate space to the equivalent one-dimensional value in order to combine it with XA, but otherwise the situation here is identical with that applying to locations B and C. It is obvious, of course, that the relation of AD to its clock space equivalent depends on the spatial location assigned to point X since the galaxy is receding in all directions, whereas the line AD has a specific direction in coordinate space.
Now let us give Figure 5 a new significance. Let us say that it represents our Milky Way galaxy instead of some distant galaxy, and that it is being depicted in coordinate time rather than coordinate space. The arrow now indicates the direction of progression of time from some assumed origin of time coordinates X. Points A, B. C, and D are locations in coordinate time within the galaxy, and are separated from one another by time intervals AB, AC, etc., which, in view of the equivalence of the unit of time and the unit of space, are commensurate with the corresponding space intervals AB, AC, etc. This equivalence enables us to measure the time intervals indirectly, but accurately, by measuring the space intervals and converting the results to the time equivalents.
We now have an exact analogy with the original significance of the diagram as indicating a galactic recession. The clock time for our galaxy as a whole, and for any individual point within the galaxy, at the stage of the time progression portrayed in the diagram is XA. The time interval between X and B is the clock time XA plus the coordinate time interval AB, making a total of XB. The time interval between X and C is XA minus AC, or XC. The time interval between X and D is XA plus or minus the component of the coordinate time interval AD in the direction XA. The magnitude of this component depends on the location of the origin X of the coordinates; that is, on the direction XA of the time progression.
This latter point is one which is somewhat difficult to grasp if we look at the time situation only, without the aid of the analogy provided by the galactic recession, because it is hard to think in terms of a time concept totally different from the one which has been handed down to us from past generations. But the recession of the galaxies, a manifestation of the space phenomenon analogous to the progression of time, is not nearly so hard to visualize. It is, indeed, quite easy to get a clear mental picture of the observed situation in which the distant galaxies are moving outward away from us in all spatial directions. The further conclusion, which necessarily follows, that our galaxy is likewise moving outward in all spatial directions away from all other galaxies, is a somewhat more difficult concept. We do not readily picture motion in all directions simultaneously, but the analogies which the astronomers use in explaining this phenomenon, such as the behavior of points on the surface of a balloon which is being expanded gradually, should help to clarify this aspect of the situation. The mere fact that the astronomical profession accepts this outward movement of the Galaxy in all directions as an established fact is, in itself, an aid to understanding, as a new idea can be more readily assimilated if there is some advance assurance that it is well-founded.
The essential point here, so far as the matters now at issue are concerned, is that the motion of the galactic recession is scalar. All galaxies, including our own, move in the same manner: outward from all other galaxies. If we wish to translate this outward scalar motion into its equivalent in three-dimensional coordinate space, we must select a point of reference, and whatever conclusions we reach concerning the coordinate space equivalent of the scalar motion are valid only for that particular reference system. If we designate our Milky Way galaxy as M, we are receding from galaxy A in the direction AM in coordinate space. At the same time we are receding from galaxy B in a different direction BM. If we wish to combine some distance CD in coordinate space with the space progression (the recession of the galaxy) we must first specify our reference system, since the component of CD in the direction AM will not be equal, unless by mere chance, to the component in the direction BM.
Similarly, the motion of the time progression is scalar. Time does not flow past us in the “unidirectional, one-valued, one-dimensional” manner which is usually “assumed without examination,” as Tolman expresses it; the progression of time is a scalar motion in a three dimensional time: each point in time moves outward from all other points in time, just as each galaxy moves outward from all other galaxies under the influence of the same kind of a progression. As long as we are dealing with matters which involve only the progression (clock time) the direction is immaterial, but when any question involving coordinate time arises, it is again necessary to have a point of reference. In the case of a beam of light, for example, the direction of the progression is from the point of origin of the beam along the path of the beam. Any conclusions involving coordinate time are valid only for this particular reference system, and may be altered very materially if the reference system is changed, as for instance, by considering some other light beam emanating from a different source.
In earlier days when physical science dealt only with relatively low velocities, the contribution of the coordinate time to the total time interval in any physical process was negligible, and it was possible to carry out all calculations involving motion on the basis of clock time only. The advent of high velocity measurements, particularly those concerned with the velocity of light, showed that there was an error somewhere in the system, and it was a study of the background of this discrepancy that led Einstein to his conclusion that, “There is no such thing as simultaneity of distant events.”81 If we are referring to total time, this present study is in full accord with Einstein’s conclusion, but for most purposes the useful definition of simultaneity is that which regards events as simultaneous if they occur at the same clock time; that is, at the same stage of the time progression, and this kind of simultaneity definitely does exist.
Einstein and his colleagues accepted the “operational” point of view in this instance and rejected the concept of an objectively real simultaneity because of its lack of an operational basis. As Moller explains, “The concept of simultaneity between two events in different places obviously has no exact objective meaning at all, since we cannot give any experimental method by which this simultaneity could be ascertained.”82 The present work shows that this conclusion is in error; that simultaneity, defined as the same clock time, is something that can be ascertained by physical means, and this concept can therefore be legitimately employed in any connection in which it happens to be useful: a category that includes most of the applications in which the idea of simultaneity is normally employed. In this sense (the only sense that is of any particular importance to us) Einstein is wrong and there is such a thing as simultaneity of distant events.
It is worth mentioning that this case illustrates the validity of one of the principal objections that is advanced against the operational viewpoint. The operational school of thought contends that no physical concept should be employed in the formulation of theory unless there are specific operations by means of which the concept can be defined. The objective of setting up such a qualification is to prevent the use of vague and misleading concepts and ideas in the construction of theory. Such an aim is hardly open to criticism per se, but the weakness of operationalism is that it is necessary to assume that if “we cannot give any experimental method by which this… could be ascertained” as the present time, we will never be able to do so; that is, there is no such method. In the present case, this assumption has been proved wrong, and it could likewise be wrong in any other instance. This does not necessarily mean that the operational idea has no merit, but it indicates that considerable care should be exercised in applying it.
XIX
Another concept which plays a major part in the detailed development of the Relativity Theory, although it is by no means a necessary consequence of the basic postulates of the theory, is that of the gravitational field. Einstein makes it clear that, so far as he is concerned, this field is not merely a mental construct or a tool of thought; it is “something physically real.” He emphasizes this point by drawing an analogy with a magnetic field where, he says, “…we are constrained to imagine—after the manner of Faraday—that the magnet always calls into being something physically real in the space around it, that something being what we call a ‘magnetic field’… The effects of gravitation are also regarded in an analogous manner.”83 In another place he tells us, “The electromagnetic field is, for the modern physicist, as real as the chair on which he sits.”84
In view of the highly critical comments that have been made and are being made about the theory of the ether, many of which imply that the originators and supporters of that theory were almost incredibly naive in believing in the physical reality of a purely hypothetical concept of whose existence no observational evidence could be detected, it is rather amusing to find the outspoken critics of the ether firmly convinced of the physical reality of the gravitational field: another purely hypothetical concept for which there is no observational evidence. The “field” theory is, in fact, almost an exact duplicate of the “ether” theory. In both cases we find matter and radiation exhibiting certain patterns of behavior that are not explained, or not completely explained, in terms of what is currently known. In order to provide some kind of an explanation of these behavior characteristics there has been invented, in each case, a purely imaginary entity having just those properties which are necessary for the purpose. In neither case is there any independent evidence of the existence of the postulated entity; it was necessary to invest both the ether and the field with certain hypothetical properties in order to explain effects that were already known to exist, but we have no indication of any other properties or any other effects of the postulated properties.
But even though these two concepts are birds of a feather almost down to the last detail, present-day theorists tell us that we should discard the ether, because there is no evidence of its existence, but that we should accept the physical reality of the field, even though this is equally without observational support. The truth is that the theory of the ether is not nearly as lacking in merit as the present-day appraisals suggest; the fact that a physicist of the caliber of P.A.M. Dirac is seriously proposing a return to the ether theory is enough to verify this point. “…the failure of the world’s physicists to find such a (satisfactory) theory, after many years of intensive research,” says Dirac, “leads me to think that the aetherless basis of physical theory may have reached the end of its capabilities and to see in the nether a new hope for the future.”85 Actually both the ether theory and the theory of the field were reasonable working hypotheses at the stage of development of scientific knowledge in which each was originally proposed, but neither is tenable as matters now stand, particularly in view of the findings of the present study.
The need for these artificial constructs—mental crutches, we might call them—has resulted from unrecognized, but equally artificial, restrictions that have been placed on the viewpoint from which physical problems have been approached. In the case of gravitation it has been taken for granted that there are only two alternatives. Either we must concede the reality of action at a distance: some mysterious power, altogether foreign to physical relationships as we know them elsewhere, whereby one mass can exert an instantaneous influence on another distant mass without any connection between the two, or else we must have some kind of a medium, an ether or a deformable space (which is simply an ether under a different name) through which the gravitational effect is propagated at a finite velocity. In this way all thinking about gravitation has been restricted to the narrow field defined by these two concepts, and since the idea of action at a distance is repugnant to most physicists, the latitude for constructive thought has been reduced to the point where the only thing left for the theorists to do is to speculate about the nature and properties of the gravitational medium. Thus Einstein rejects the ether and gives space the properties of a medium. Then when Dirac is disillusioned with Einstein’s theories and concludes that they have arrived at a dead end, he sees no alternative but to return to the ether as “a new hope for the future.”
But in spite of the unquestioning acceptance of the existence of this dilemma in present-day science, these are not the only alternatives. The development of the Reciprocal System leads to another explanation altogether different from the two which have hitherto been regarded as the only possibilities, and examination of this new hypothesis not only shows that it is a consistent and wholly logical explanation of the observed facts, but also reveals that there are other physical phenomena which behave in a similar manner, and hence this is not even a novelty; it is something that has been in plain sight all the time, but has not heretofore been recognized as being applicable to the gravitational situation. We are very familiar with the aftermath of an explosion, in which the individual fragments of debris are moving outward away from each other as if they are subject to a force of mutual repulsion. We also find the galaxies behaving in a similar fashion as if they are subject to a repulsive force: the force of cosmic repulsion as it is sometimes called. We recognize in these instances that just because the individual units behave as if mutually generated forces are acting upon them, we do not necessarily have to conclude that a mutual action actually exists. Here we take the stand, definitely in one case and somewhat tentatively in the other, that there is no mutual action, that each individual unit is pursuing its own independent course and that the interaction is only apparent and not real. Obviously this same explanation could apply to any case where individual units behave as if they are subject to mutual forces. The prevailing belief that we are forced to choose between action at a distance and propagation through a medium (or a medium-like space) is therefore erroneous; we have a third alternative, and the development outlined in the preceding pages indicates that this third alternative is in agreement with the observed facts at all points.
This new explanation completely eliminates all justification for postulating the existence of a gravitational field as “something physically real.” It accounts for all aspects of the gravitational phenomenon in terms of the motion of the individual mass units, without any participation by either a medium or a field. It is legitimate to use the term “field” to describe the region in which the gravitational effect makes its appearance, and to call the magnitude of this effect at any specific location the “strength of the field” at that point. But this is merely an artificial method of expression adopted for convenience: “nothing more than an aid in the calculations that have to be performed,”29 as McVittie expresses it. The so-called “field” neither acts upon matter nor is itself acted upon by matter.
When the concept of the gravitational field as a physically real entity goes into the discard it automatically carries with it the deformation of space which, according to current theory, creates the field. Actually it is very difficult to distinguish the present-day concept of “space” from that of the “field” or, for that matter, from the concept of the “ether.” At first glance these appear to be altogether different entities, but when a closer analysis is made, to determine just how each of these concepts fits into the picture as a whole, the differences tend to disappear. Eddington makes the following comment, referring to the distinction between field and space: “The distinction thus created is a rather artificial one which is unlikely to be accepted permanently.”86 At the same time, it is commonly recognized that the distinction between the ether and the present-day concept of space is almost entirely verbal. As R. H. Dicke puts it, “One suspects that, with empty space having so many properties, all that had been accomplished in destroying the ether was a semantic trick. The ether had been renamed the vacuum.”1 Marshall J. Walker says flatly, “The distinction between “space” and “ether” is largely semantic.”87
Two general concepts of the nature of space have come down to us from the philosopher-scientists of antiquity. One viewpoint—that held by Aristotle—regards space merely as a relationship between material objects, while an opposing view, favored by Democritus and his fellow atomists, regards it as a container in which these material objects exist. Neither of these concepts provides any connection between the objects; on the contrary, they are merely different ways of looking at the discontinuity between them. As scientific knowledge expanded, however, more and more phenomena were discovered which the scientific profession was unable to explain without some kind of a physical connection between these material objects: the transmission of radiation, the existence of gravitational effects, electric and magnetic phenomena, etc. The concept of the ether was therefore invented to meet the requirements of this situation. As originally conceived, this ether was a substance pervading all space in somewhat the same manner that the air fills the otherwise unoccupied space in our local environment. It then constitutes the connecting medium through which the various effects are transmitted.
The principal weakness of the ether theory, aside from the total lack of any independent evidence of the existence of anything of this kind, is that when the ether is postulated to be a “substance” it becomes identified with material substances, whereas the properties which it must have in order to perform the functions for which it was invented are incompatible with those of material substances. It must, for example, be more rigid than steel, in order to account for the transverse vibration of electromagnetic radiation, but at the same time it must be even more fluid than the lightest gas, in order that material objects may move through it without frictional effects. What Einstein and his colleagues have done is to attribute to space all of the properties that were previously conceived as properties of the ether. Thus the utility of the ether as a medium is retained—space itself has now become a medium—but inasmuch as this medium is no longer identified as a “substance” there are no longer any restrictions on the kind of properties that can be postulated. Who can say for instance, that a rigid space is incompatible with the absence of friction?
The difficulty of distinguishing between the concepts of “space,” “field” and “ether” is a result of the fact that, as currently employed, all three terms refer to the same thing: the hypothetical universal medium. The significant properties that are attributed to these entities, the properties that are actually needed for the performance of their assumed physical functions, are the same in all cases; the only differences between them are in connotations of the language employed that are carried over from the sources from which that language was derived, but have no meaning in the terms of reference of current theory. The word “field,” for instance, calls up a considerably different conceptual image than the word “space,” yet if we examine the way in which each word is used in present-day physical theory, we are compelled to agree with Eddington that any distinction between the two is purely artificial.
The present confusion in this area is largely chargeable to Einstein. Before his day the accepted world picture included an ether located in and coextensive with space. It is commonly contended that Einstein’s system eliminated the ether and accounts for gravitation as a product of the geometry of space, but in reality what he did was to eliminate the name “ether” and the concept “space.” The entity to which he applies the name “space” is the same one that was previously called the “ether.” His “space” has all of the properties that were formerly assigned to the ether concept: properties that are altogether different from those of the previous concept of space, and likewise totally unlike the properties which we are able to recognize in space where we are in a position to observe it.
Even Einstein himself was forced to admit that the ether still exists in his system: “…we may say that according to the general theory of relativity space is endowed with physical qualities; in this sense, therefore, there exists an ether.”88 In another connection he elaborates, “But therewith (through the General Theory) the conception of the ether has again acquired an intelligible content, although this content differs widely from that of the ether of the mechanical undulatory theory of light. The ether of the general theory of relativity is a medium which is itself devoid of all mechanical and kinematical qualities, but helps to determine mechanical (and electromagnetic) events.”89 Elsewhere we find this significant admission: “We shall say: our space has the physical property of transmitting waves, and so omit the use of a word (ether) we have decided to avoid.”90
In these three statements the contentions advanced in the preceding paragraph as to the true nature of the manipulation of space and ether in the Relativity Theory have been confirmed by the author of the theory. Einstein admits that it is only the name “ether” that he has discarded and that the functions of the ether have been transferred to space, thus making space a medium. The fact that he specifically uses the word “medium” is particularly significant.
The view of space as the discontinuity’ between physical objects, which is basic in both of the traditional concepts of the nature of this entity and which is the essence of the meaning attached to the word “space” in everyday usage, has now been discarded, and space has become the connecting medium between the objects. “There is then no ‘empty’ space,” Einstein asserts, “that is, there is no space without a field.”91 Thus a totally new concept of space has been introduced.
Then, to compound the confusion, Einstein insists that in the General Relativity Theory gravitation is solely a result of a deformation or curvature of this redefined space, resulting from the presence of mass, and he makes it clear that in his opinion he has reduced gravitation to a property of space-time. Yet he is equally insistent that the gravitational field is, as he puts it, “something physically real in the space.” Here again is a direct contradiction similar to the one pointed out in connection with the mass-energy relations. If gravitation is simply a geometrical effect, as Einstein claims, there can be no “physically real” entity which produces gravitational effects; if there is a physically real gravitational field “in the space” as Einstein also claims, then gravitation is not a purely geometrical affect. He cannot have it both ways. If it were not for the “exceedingly complex and difficult” nature of the General Theory, which has insulated it against effective criticism, both this and the equally glaring conflict in the mass-energy relations no doubt would have been recognized long ago.
In retrospect it is clear that gravitational theory was diverted into the wrong channel at the very beginning of its development by the uncritical acceptance of the concept of gravitation as an action of one mass upon another. No subsequent skill or ingenuity could compensate for such a serious initial error, and the “failure” of the currently accepted theory to which Dirac refers in the statement previously quoted was inevitable from the start.
Einstein presents one independent argument in support of his “curved space” hypothesis which deserves special comment. He points out that a gravitational force following the inverse square law in an Euclidean universe is incompatible with a uniform or approximately uniform density of matter. On such a basis, he says, “The stellar universe ought to be a finite island in the infinite ocean of space.”92 A. C. B. Lovell elaborates the same thought in these words: “The application of Newton’s theory of gravitation, in which the attraction between bodies varies inversely as the square of their distance apart, to the large-scale structure of the universe would require that the universe had a center in which the spatial density of stars and galaxies was a maximum. As we proceed outwards from this center the spatial density should diminish, until finally at great distances it should be succeeded by an infinite region of emptiness.”93
It is evident that the observed universe does not conform to this theoretical condition that would result from the assumed premises, and Einstein therefore arrives at the conclusion that space must be curved so that it is finite in extent even though unbounded. But this argument contains a hidden assumption: the assumption that the gravitational force of each individual mass is effective over infinite space. According to the new information presented herein, this is not true. There is a gravitational limit for each mass and a net gravitational force exists only within this limit. Einstein’s argument is therefore valid only for the region within the gravitational limit of each mass aggregate, and in each of these regions the observed behavior is just what he claims it would be if space is Euclidean; that is, each galaxy and each star system (single star or multiple star system) is a “finite island in the ocean of space” defined by the gravitational limits of that galaxy or star system. Even before the true nature of the external galaxies was definitely established, Kant and others were referring to these objects as “island universes.” Einstein’s point therefore not only ceases to be a valid argument against Euclidean space, but becomes an argument in favor of the Euclidean system.
XX
One of the most frequent comments offered by those who have become acquainted with the gravitational theory of this work through previous publications concerns the relatively minor use of mathematics in the development. “I am particularly puzzled about the lack of mathematics associated with your methods,” writes a British correspondent, “surely in order to show the superiority of your theory you must be able to predict all the experimental facts explained by present theories and more. It is difficult to see how you will do this without setting the whole thing on a rigorous mathematical basis.” Another correspondent asks, “Can you put your theories into a tensor formulation?”
These comments reflect a general misconception that has developed in science, particularly in physics, within the present century, in which the “rigor” of the mathematical treatment is judged on the basis of its length and complexity, not on the basis of its adequacy for the task at hand. Following Einstein’s lead in calling upon complex mathematics in an attempt to compensate for conceptual errors, present-day physical theory has become largely a juggling of abstract mathematical relationships, the meaning of which (if any) “we do not ask,” as Eddington says. As so often happens when form is overemphasized, form rather than substance has come to be regarded as the essence. To arrive at a result in the realm of basic theory by plain arithmetic or simple algebra is today unthinkable; unless we can express that result in terms of tensors, or spinors, or matrix algebra, or some other currently fashionable mathematical device, it is automatically unacceptable.
How far would Newton get today with his gravitational equation? Could such a simple expression as
$$F = G \frac{m m'}{d^2}$$
ever hope to receive any consideration from a generation of physicists accustomed to tensors of the fourth rank? Obviously not. But this simple and unpretentious equation is the only practical expression of the gravitational effect ever formulated: the only one that gives us answers to real problems. To the engineer gravitation and Newton’s Law are synonymous, and as Einstein himself admits in the statement previously quoted, this simple law “still remains the basis of all astronomical calculations.” What this present work has done is to show that this simple expression that gives such remarkably good results in all practical applications is an exact statement of the theoretically correct relationships and that, in its proper context, it is universally applicable. On this basis there is no need whatever for any new mathematical development; Newton gave us all of the necessary mathematics three hundred years ago. Simple as his expression is, the present analysis indicates that it cannot be improved upon.
The gravitational theory derived from the postulates of the Reciprocal System is Newton’s gravitational law. The detailed development of this theory shows that the objections that have been lodged against Newton’s Law by modern investigators are based on erroneous conclusions, and that his gravitational equation is actually valid throughout the universe, precisely and with no exceptions. As has been pointed out previously, the only one of the items of evidence currently offered in support of Einstein’s proposed modification of Newton’s gravitational ideas that can stand up under critical scrutiny is the advance of the perihelion of Mercury, and the new information developed in this work shows that this is due to the high velocity of the planet and has no connection with gravitation. It is a result of the same factors which are responsible for the negative outcome of the Michelson-Morley experiment, not of any deficiency in the gravitational law.
The other objections of a less tangible nature that have been advanced against Newton’s theory have been similarly overthrown. Eddington lists three such objections.65 “The most serious objection against the Newtonian law as an exact law was that it had become ambiguous,” he tells us, and then continues with the statement previously quoted in part, “The law refers to the product of the masses of the two bodies; but the mass depends on the velocity—a fact unknown in Newton’s day.” Even without the evidence from the present work which shows that mass does not depend on the velocity, it is obvious that this is not a “fact” ; whenever such a statement is challenged it has to be admitted that this concept of an increase in mass is purely an arbitrary selection from among several possible explanations of the experimental facts. Here is a good illustration of the extreme lengths to which modern physicists have gone in their attempt to build up a case against Newton. When the “most serious objection against the Newtonian law” is based on a totally unsupported assumption it is evident that the other objections must be flimsy indeed.
Such a conclusion is fully justified by Eddington’s next objection, which is that Newton’s theory is incompatible with a finite velocity of propagation of the gravitational effect. “In the theory given in this book,” he says, “gravitation is propagated with the speed of light…” In other words, Newton is wrong because his assumption does not agree with Eddington’s assumption. This present work demonstrates that gravitation is not propagated with the speed of light, nor is it propagated instantaneously; it is not propagated at all: a fact which is fully compatible with Newton’s theory. Likewise this work disposes of Eddington’s third objection: “Further, distance, also referred to in the law, is something relative to an observer…”
In the simple, completely understandable world of the Reciprocal System all of these present-day objections are swept away and Newton’s gravitational equation is valid throughout the universe, from the smallest region to the largest. Where, then, is there any place for complex mathematics? Do we need to call upon matrix algebra or tensors to restate the Newton equation? The whole idea of a more “rigorous” mathematical foundation is preposterous. If the mathematics at hand are fully adequate for their purpose there cannot be anything more complete or more rigorous, even if the mathematical formulation amounts to nothing more than a statement that two plus two equal four. Once it has been established that the Reciprocal System leads to Newton’s gravitational law and that it demolishes the objections that have hitherto been raised against the universal validity of that law, there is nothing further for mathematics to do. Newton’s equation cannot be made any simpler and nothing can be gained by expressing it in a more complex manner.
Present-day basic physical theory does not need more mathematics—it is overflowing with mathematics already. What it needs is a conceptual clarification that will enable making full use of the physical knowledge and the mathematical tools already available. This is the objective of this present work: not to add to the profusion of abstruse mathematical speculations now in existence, but to identify the conceptual errors in the previous development of theory and to point the way to the changes in thinking that are necessary in order to make full use of the mathematical and theoretical equipment already on land.
It is not contended here that all phases of Newton’s system are universally valid; on the contrary, the Reciprocal System agrees with currently accepted physical theory in the conclusion that Newton’s Laws of Motion must be modified in application to high velocities. Again, however, there is no need for any elaborate mathematical development. The Reciprocal System raises some serious questions as to whether any useful purpose is served by expressing the high velocity relationships in terms of clock time, in accordance with current practice, but if any such purpose exists, this system leads directly to the same mathematical expressions—the Lorentz transformations—that are utilized by currently accepted theory. Once again, therefore, we find the necessary mathematics already in existence, and further mathematical development is wholly superfluous.
At this point it should again be emphasized that the mathematical aspects of Einstein’s Special Theory did not originate from that theory; they are purely empirical relations which were current in physical circles before the Relativity Theory was formulated. The Michelson-Morley experiment showed that the velocity of light is independent of the reference system. This made it clear that if the existing concepts of space, time and motion were to be retained, a variation of distance (and perhaps time) with velocity must be introduced, and the amount of the necessary variation can be readily calculated in a straightforward manner from empirical data. Such a calculation led to the conclusion that distance magnitudes are reduced by the factor (1-v2/c2)1/2 when bodies in motion are observed from a reference system at rest, whereas the corresponding time magnitudes are increased by the same factor. As an empirical relationship, this result is obviously valid regardless of the theoretical approach that is employed and no theory is acceptable unless it arrives at the same or an equivalent result.
This answer to the problem is conceptually wrong; that is, space and time magnitudes are in fact absolute and a change in reference system does not alter them, other than to introduce the differences between the coordinates of the reference systems. Time does not pass more slowly in a moving system nor does space contract. But for this special case, where the relative motion is uniform and translatory, the correct numerical results can be obtained by assuming a fictitious contraction of space and dilatation of time, and what Einstein did was to set up the mathematical and theoretical framework of a system that would accomplish this result. In spite of the fact that this system is conceptually wrong, it is mathematically correct for this special case. Obviously it must be correct if the error in using clock time only is a function of the velocity, since the correction factor was obtained empirically.
Let us now examine the theoretical basis of this empirically determined correction factor. According to the principles of the Reciprocal System, the distance measured on the basis of Euclidean geometry is the true coordinate distance regardless of velocities and irrespective of the system of reference (as long as the reference system qualifies as a legitimate one on the basis of the criteria previously specified). In any application within our own galaxy, where we do not have to take the galactic recession into account, we are dealing with coordinate distance only, and hence this measured coordinate distance is also the total physical distance.
Similarly, the time measured by any accurate clock is the true clock time irrespective of whether the system of reference in which the clock is located is stationary or in motion, and thus the clock time interval is also an absolute magnitude. But when an object is in motion it is not only moving in clock time, the quantitative expression of the motion of the progression, a motion that all material objects participate in, even when they are at rest in our usual system of reference, but is also moving in coordinate time, analogous to coordinate space. If we are dealing with the velocity of light, which is one unit of space per unit of time, any points which are separated by n units of coordinate space are also separated by n units of coordinate time. This coordinate time difference is separate and distinct from the clock time and must be added to the clock time to obtain the true physical time, just as we had to add the random motion of the distant galaxy to the motion of the galactic recession before we could determine where the galaxy would actually be found. It is evident that the velocity of light is always unity in such a system, but it is likewise clear that when we take the coordinate time into consideration as well as the clock time, there is no conflict between the constant velocity of light and the absolute magnitudes of the space and time intervals involved.

Figure 6
Inasmuch as any material particle is continually passing from one unit of space to another (since it is moving against the direction of the space-time progression) and the direction of the progression of each new unit is indeterminate, the motion of such a particle is distributed equally in all spatial directions. Radiation in free space, on the other hand, maintains the same spatial direction indefinitely, as the photon has no independent motion of its own. It follows that whether a particle is in motion or at rest relative to our usual reference system, and regardless of what direction in coordinate space any such motion may take, the particle is moving with the progression, and hence with the radiation, half of the distance that it travels and opposite to the direction of the radiation during the other half. We may therefore treat any movement of light or other radiation relative to material objects as if it involved a round trip, irrespective of the situation that may prevail in the usual system of reference.
Let us assume that a light signal originates at point A on a rigid rod AB which is in motion toward the right of the diagram, Figure 6, with velocity v. The light signal travels to the point B. which in the meantime has moved forward to B’, and here it is reflected back. By the time it completes the round trip, point A has moved to A’, and the round trip is AB’A’ rather than ABA. If we analyze this situation on the basis of the assumption (accepted by both Newton and Einstein) that physical time consists of clock time only, the distance traveled by the signal is ct. since we have found from experiment that the velocity of light is constant irrespective of the reference system. The time t, according to Newtonian principles, is the distance AB, which we will call s, divided by the net velocity c-v on the outward trip and the same distance divided by the net velocity c+v on the return trip This gives us
$$t = \frac{s}{c - v} + \frac{s}{c + v} = \frac{2 s c}{c^2 - v^2}$$
Multiplying by c, we then have the distance traveled:
$$\frac{2 s c}{c^2 - v^2} \times c = \frac{2s}{1 - \frac{v^2}{c^2}}$$
At rest, the round trip distance ABA is 2s. Now we find that if we insist on expressing our results in terms of clock time only, we must introduce a mathematical correction equivalent to reducing distances applying to objects in motion by the factor 1-v2/c2, in order to be consistent with the distances measured at rest. Since space and time are reciprocally related in velocity, the correction does not necessarily have to be applied to the distance; it can be applied either to distance or to time or to both. In the light of the points developed in this volume it would be most logical to apply the correction to time, since it is through a misunderstanding of the nature of time that the whole difficulty arises, but as the Relativity Theory actually developed, the correction was divided equally between space and time, the distance being reduced by the factor (1-v2/c2)1/2 and the time extended by the reciprocal of this factor.
As indicated in the preceding discussion, the advance of the perihelion of the planet Mercury, which is commonly interpreted as indicating a deficiency in Newton’s gravitational law, is actually a result of the same misconception of the nature of time that the Special Theory tries to compensate for. The orbital velocity of Mercury is approximately 29.8 miles/sec, which, in terms of the velocity of light as unity, is .00016. The correction for the coordinate time, v2/c2, is then 2.56×10-8; that is, the clock time must be increased by this factor. Since the gravitational motion is inward, the scalar space-time direction of the orbital motion is outward, and the computed time increase is radial. To obtain the circumferential space equivalent of this linear time increase, we multiply by π obtaining 8.04×10-8, or 0.1042 seconds of arc per revolution. This amounts to 43.35 seconds per century, which agrees with the observed advance of the perihelion, within the accuracy of the measurements. Tolman reports 43.5 seconds per century as the observed value and 42.9 seconds per century as the result obtained by calculations based on the Relativity Theory.
XXI
In connection with this discussion of the incidental aspects of the gravitational situation, it may be in order to make some comments about the methods of approach to the problem which were utilized in the construction of the three theories that have been discussed: Newton’s Law, Einstein’s General Theory, and the gravitational theory derived from the Reciprocal System.
Newton’s gravitational theory was developed during a relatively early scientific era in which basic physical concepts were simple and direct. When and if a theory became inadequate the corrective measures were applied to the basic concepts; these were drastically modified or else discarded and replaced by other simple and direct concepts. Einstein’s General Theory, on the other hand, is a product of the more sophisticated and ingenious modern school, which relies upon mathematical techniques to fit existing concepts to the observed facts rather than giving up basic ideas which encounter trouble. If a theory which agrees with the observed facts in a restricted area fails in application to a broader field there is, of course, a very strong probability that the theory is in error in some important respect. But abandonment of a cherished theory or concept is extremely distasteful, not only to the author of the theory, but also to those who have accepted it and have based their own thinking upon it, and in recent times the tendency has been to call upon an increasingly numerous assortment of devices whereby the theories can be made “looser” and accommodated more readily to a wider range of observational data, thus avoiding the painful necessity of parting with familiar and comfortable habits of thought.
One of the easiest ways of avoiding conflict with the facts is to make the theory less specific. At the present time, for example, there is a great deal of activity that is directed toward the construction of semi-theoretical mathematical expressions designed to represent physical properties of matter. The usual practice is to start with some purely theoretical relation, such as the general gas law PV = RT. In order to secure better agreement with the experimental results this relation is then modified by additional terms and adjustable constants. In developing the first “equation of state” for gases from the general gas law, Van der Waals used two such constants. For a better fit with the experimental data, subsequent equation constructors have increased the number of these adjustable or “disposable” constants. The Beattie-Bridgman equation has four; the Benedict-Webb-Rubin equation has eight.
If the objective of this activity is the attainment of close agreement with the experimental values for the purpose of facilitating interpolation and extrapolation of the experimental results, the prevailing policy has been successful, since the correlation is, in general, increasingly better as the number of constants is increased. But if the objective is to ascertain the correct relationships and numerical values, this program of increasing the flexibility of the equation by adding more and more adjustable constants is definitely proceeding in the wrong direction. Every added constant makes it easier for the equation to fit the experimental data, to be sure, but in so doing it correspondingly decreases the probability that the equation and the results obtained from it are correct. This is an inescapable mathematical consequence of the increase in the number of possible variations of the experimental data which will agree with the equation.
In order to make progress toward the correct answers it is essential to reduce rather than increase the adjustability of the equation. As we move in this direction we must obviously keep the results of the calculations within the limits of experimental uncertainty, and we can move only as fast as we are able to devise new modifications that will stay within those limits, but as long as this requirement is met, every additional restriction that can be placed on the quantities entering into the calculations increases the mathematical probability that the values obtained from these calculations correctly represent the true physical magnitudes.
The difficulty with this line of approach is that it is the hard road to follow. The prevailing practice of increasing the flexibility of the mathematical expressions through the addition of more adjustable constants or similar means follows a well-defined path: one which is almost certain to achieve results of some kind if sufficient time and effort are applied to the task. Most attempts to make progress toward the difficult goal of a more restrictive equation, on the contrary, will inevitably end in nothing but frustration and disappointment, and ordinarily no really significant advance can be made without discarding some cherished idea of long standing. The preference for the easy route is therefore quite understandable, but here, as in so many other lines of human endeavor, true forward progress can only be made in the hard way.
The situation in such areas as gravitational theory is not quite as obvious as that which results from the addition of successive adjustable constants to the equations of state, but any measure that increases the flexibility of a theoretical relationship so that it can more readily accommodate itself to the experimental data produces the same results as these added constants: it increases the number of possible situations which can be made to agree with the postulated relation and hence decreases the mathematical probability that the relationship is correct. A theory such as Special Relativity which denies the constancy of the magnitudes of space and time intervals has a smaller probability of being correct than one which accepts fixed space and time magnitudes, providing that neither is inconsistent with the observed facts. A theory such as General Relativity which goes still farther in the same direction and eliminates the “metrical meaning” of the coordinates that are employed in describing these magnitudes has a still lower probability of being correct, and if Einstein had succeeded in his attempt to devise a general field theory by further loosening of the theoretical structure along similar lines, the a priori probability of the validity of such a theory would have been essentially negligible.
In this connection, Bondi makes the comment, “…it may justifiably be asked at this stage, when the mathematical complexity of the theory emerges, why Einstein should require ten potentials of gravitation where one was good enough for Newton.”94 The answer is, of course, that instead of locating and correcting the error in the basic space-time concepts of Newton’s gravitational theory Einstein set up a looser and more flexible theory that can be stretched far enough to cover the observational facts with the error left intact. His gravitational potentials serve exactly the same purpose as the eight adjustable constants of the Benedict-Webb-Rubin equation of state; in both cases mathematical flexibility is substituted for a correct conceptual foundation.
Every ad hoc assumption that is made in the construction of the theory has the same kind of an effect on the probability of the validity of the theory as the addition of one of these adjustable constants or potentials. Since there is no independent evidence of a deformability or curvature of space, any theory which postulates such a property has a lower probability of being correct than one which does not have to resort to an unsupported postulate of this kind, other things being equal. The same is true of any other ad hoc postulate. Here again, as in the formulation of equations of state and similar mathematical expressions, true forward progress toward the ultimate goal can come only by way of an increasingly restrictive approach: one which decreases, rather than increases, the employment of ad hoc assumptions. This ultimate goal, as defined in Part One, is a verifiable first order explanation: a theoretical structure which is based solely on simple assumptions as to fundamental properties of the universe, the validity of which can be independently confirmed, and which is consistent with all positively established facts in its field, without exception. Such a theory, by definition, cannot rely upon any ad hoc assumption anywhere in the line of development. Progress toward that theory must therefore involve a reduction in the amount of reliance placed on such assumptions, either by eliminating the need for certain assumptions, or by deriving their substance from the basic postulates of the theoretical system, so that they no longer have the ad hoc status.
The validity of the foregoing assertions is practically self-evident. Such ideas are, however, given scant consideration in current scientific thinking, not because of any disagreement in principle with the contention that this is the true route toward a complete, logical and understandable theory if such a theory exists, but rather on the ground that such a goal is an impossible one. There is a very general tendency to extrapolate it has not been done to it cannot be done and to conclude that whatever science has failed to accomplish after making a serious attempt must be unattainable. As Philipp Frank expresses the current attitude, “the belief that science will eventually reveal the ‘truth’ about the universe” is a nineteenth century idea that “broke down” during the last decades of that century.95 Those who adopt this viewpoint realize that their conclusions will be met with amazement and incredulity outside of their own circle. “To the outsider,” says Henry Margenau, “the conclusions reached by a modern physicist seem almost like a declaration of the bankruptcy of science.”96 But the “modern physicist” cannot envision the possibility that this outside viewpoint may be a correct appraisal of the situation and that he and his colleagues may be on the wrong track. Margenau merely reflects the general sentiment of the scientific community when he assumes as a basis for an extended consideration of the problem of formulating physical theory that a comprehensive, clearly understandable general physical theory is impossible.
From this premise he then reasons that we have two alternatives. One possibility is to utilize some intelligible model as far as it will go, and then set up additional, probably incompatible, models of the same kind to cover the areas outside the scope of the original model. This was the idea expressed by Jeans: “The most we can aspire to is a model or picture which shall explain and account for some of the observed properties of matter; where this fails, we must supplement it with some other model or picture, which will in its turn fail with other properties of matter, and so on.”97 The second alternative, according to Margenau, the one which he favors personally, is to achieve more generality by making the theory more abstract. In following this line of development “models lose their… intuitable features; in short, abstractness is the price science pays for embraciveness of conception.”98 This is the philosophy of the two major theoretical developments of recent times: Relativity and the various quantum theories.
When we subject Margenau’s conclusions to a critical examination, however, it is apparent that the so-called trend toward abstraction is not so much a matter of making the theory more abstract, but of making it more flexible, so that the theorist can meet further demands on his constructions without having to face the distasteful necessity of altering any of his basic concepts. The Special Theory of Relativity, for example, did not produce the correct results when applied to non-uniform motion, hence Einstein introduced some further flexibility—abandoning the “metrical meaning” of his coordinate systems, and abandoning the fixed and determinate Euclidean geometry in favor of a geometry of variable space curvature—in order to stretch the basic elements of the Special Theory far enough to cover the more general situation. As he explains, “But in sketching the way in which it (the construction of the General Theory of Relativity) was accomplished we must be even vaguer than we have been so far. New difficulties arising in the development of science force our theory to become more and more abstract.”99 The word “abstract” is thus being used as a synonym for “vague.”
But all this is a means of evading the issue, not of meeting it. If Newton’s Laws of Motion do not give the right answers in application to bodies moving at high velocities, the clear implication is that there is some error in the basic assumptions underlying these laws, as Einstein recognized. If the Special Theory of Relativity fails to give the right answers in application to non-uniform motion, the equally clear implication is that there is an error in the basic assumptions of this Special Theory, but Einstein was not willing to accept, in application to his own theory, the conclusion which seemed so clear to him so far as Newton’s system was concerned, and the introduction of more flexibility or abstraction was simply a way of avoiding the necessity of facing this uncomfortable situation.
It is quite understandable that the author of a theory that has received general acceptance and widespread public acclaim should be reluctant to concede that there are fundamental defects in this theory and should resort to every possible expedient to save this invention that has brought him fame, but there is no good reason why the scientific profession as a whole should meekly acquiesce in a course of action dictated by proprietary pride rather than by scientific considerations, and Einstein should not have been permitted to run away from the problem. In order to arrive at the correct answer, it is obviously necessary to move in the opposite direction from Einstein’s course: to ascertain just where the basic assumptions are wrong and then to make the appropriate correction. As the findings of this work indicate, Einstein was right in his conclusion that there is an error in the basic assumptions of Newton’s Laws of Motion, but he was wrong in his conclusion as to the location of the error and the measures that were required in order to correct it, and his insistence on maintaining his original constructions intact at all costs has simply blocked all progress toward the correct answer. Actually both Newton’s Laws of Motion and the Special Theory of Relativity foundered on the same rock: an erroneous concept of the nature of time. No amount of additional “abstraction” can compensate for such a basic error, except in the very simplest situations.
Modern theorists pride themselves on having eliminated the “rigidity” of previously existing scientific concepts. Heisenberg states the case in these words: “Coming back now to the contributions of modern physics, one may say that the most important change brought about by its results consists in the dissolution of this rigid frame of concepts of the nineteenth century.”100 But this “rigid frame” is one of the prerequisites for true progress; any change should be in the direction of more rigidity rather than less. As long as the experimental evidence shows that the gravitational action is instantaneous and that there is no medium, nothing of any real value can be accomplished by evading the “rigidity” of these observed facts and constructing a theory “floating in air” as modern practice has been described. No genuine forward progress can be made in this area unless a theory based on instantaneous action without a medium can be devised, and until such a theory makes its appearance (as it now has) the only sound policy is to follow Newton’s example and accept the empirical facts with the realization that their underlying significance is unknown, however great a blow this may be to the ego of the theorist. Attempts to circumvent these observed facts by greater abstraction or mathematical manipulation are futile; they simply direct the time and effort of the scientific profession into channels that lead nowhere.
The development of the consequences of the postulates of the Reciprocal System has now demonstrated that Newton was right: that an explanation can be found for gravitation which accounts for all of the observed characteristics of this phenomenon in terms of the familiar concepts of everyday experience, without any medium and without action at a distance. The mere existence of this third alternative automatically invalidates all constructions based on the argument that only the two previously recognized alternatives are available. It is now obvious that the present-day policy of maintaining basic physical theories intact at all costs—by abstraction or other evasive devices—has accomplished nothing in this instance but to postpone the day of reckoning and to waste countless hours of scientific effort. Physics would have been far better situated now if the “rigid frame” of pre-Einstein theory had been maintained and the time and effort of the scientific profession had been channeled into activities directed toward identifying and correcting the error in the basic premises of gravitational theory, instead of being devoted to fruitless wanderings in a maze of complex mathematics and abstract theoretical concepts.
XXII
In Newton’s era it was generally agreed that physical theory was to be derived from experiment and observation in the first instance, and that the development of such theory was essentially a matter of applying mathematical and logical processes to the basic information derived from these physical sources. As Einstein describes the situation, “…the scientists of those times (the 18th and 19th centuries) were for the most part convinced that the basic concepts and laws of physics were not in a logical sense free inventions of the human mind, but rather that they were derivable by abstraction, i.e., by a logical process, from experiments.”60
Einstein asserts, however, that we cannot get a true picture in this way: by observation or by theoretical constructs based on observation. “Since, however, sense perception only gives information of this external world or of ‘physical reality’ indirectly,” he says, “we can only grasp the latter by speculative means,”101 and he specifically condemns Newton’s line of approach in these words, “Newton… still believed that the basic concepts and laws of his system could be derived from experience… the tremendous practical success of his doctrines may well have prevented him and the physicists of the eighteenth and nineteenth centuries from recognizing the fictitious character of the foundations of his system.”102 Elaborating this thought in another connection, he continues, “The theoretical scientist is compelled in an increasing degree to be guided by purely mathematical, formal considerations in his search for a theory, because the physical experience of the experimenter cannot lift him into the regions of highest abstraction.”103
In these statements Einstein is advancing the curious contention that it is possible to derive from purely theoretical processes specific information about the physical world that cannot be obtained, directly or indirectly, from observations of the physical world itself. One might hesitate to believe that he actually meant what these statements seem to say, were it not for the fact that he repeats them over and over, and acquiesces in interpretations of his views such as that of F. S. C. Northrop, who states plainly, “It has been noted that the basic concepts of deductively formulated scientific theory as conceived by him (Einstein) are neither abstracted from nor deduced from empirically given data… they are concepts of a kind fundamentally different from the nominalistic particulars which denote data given empirically… And because the theoretic term cannot be derived from the empirical term, theoretic physics contributes something of its own to the scientific conception of nature and reality.”104 Einstein’s approval of this statement may be inferred from his high praise of the article in which it appeared. “I see in this critique,” he says, “a masterpiece of unbiased thinking and concise discussion, which nowhere permits itself to be diverted from the essential.”105
Here is strange doctrine indeed. Even the Kantian concept of a priori knowledge, which asserts that we have an inherent perception of certain truths that makes physical observation unnecessary in these particular areas, does not go anywhere near this far. Kant’s viewpoint does not claim that there are facts of nature, which cannot be determined from observation; it merely contends that observation is superfluous in these particular instances. Now we meet the strange contention that. The information, which we derive directly from experience, is “fictitious” and that theoretical processes can give us authentic information about the physical world, which cannot be obtained by observation or by logical processes based on such observation. Modern physical science has lived in its dream world of “free inventions” and mathematical theories “floating in air” for so long that, like any individual who withdraws from reality and builds his own world of fantasy, the scientist has now arrived at the stage where the phantoms of his imagination seem real and the physical realities appear fictitious.
The truth is that this contention that there are physical facts which are inherently beyond our ability to observe or measure, or to ascertain by mathematical or logical processes based on such observation or measurement is preposterous. Perhaps there are some facts which are beyond the capabilities of existing methods, but even this is a highly questionable assumption as there is little reason to believe that we are anywhere near the point of having exhausted the potentialities of the methods now available. Furthermore, the possibilities in the way of developing new methods are, so far as we are aware, essentially unlimited. We cannot say, therefore, in any particular case that it is impossible to devise a method that will serve our purpose. Hence, if the theoretical processes furnish “something of their own”—some information which cannot be “abstracted or deduced from experimentally given data”—this is not information about the physical world. If it has any meaning at all, it is simply information about the theory, or the model, which has been set up to represent the physical reality. It belongs to the dream world, not the real world.
The question then naturally arises, how did a scientist of Einstein’s competence ever come to formulate such an upside down viewpoint as this: a viewpoint from which the data of experience are “fictitious” and only the “free inventions of the human mind” can represent “physical reality”? Fortunately for the peace of mind of future historians of science, who would otherwise be confronted with a baffling enigma, he supplies the answer himself. “It was the General Theory of Relativity which showed in a convincing manner the incorrectness of this view,” he says, referring to his description of the 19th century viewpoint previously quoted. He points out that Newton’s theory agreed with the facts over a very wide area, and that the General Theory achieves a still wider range of agreement, over most of which it also agrees with Newton’s results. Thus it is possible to obtain “a large measure of agreement with experience” from two widely different bases, from which fact he draws the conclusion: “This indicates that any attempt logically to derive the basic concepts and laws of mechanics from the ultimate data of experience is doomed to failure.”60
To Einstein, the lover of pure theory, already strongly predisposed to regard his theories as something more than mere tools of thought (”To him who is a discoverer in this field the products of his imagination appear so necessary and natural that he regards them, and would like to have them regarded by others, not as creations of thought but as given realities” ),106 this was enough. “…The axiomatic basis of theoretical physics cannot be an inference from experience, but must be free invention…”60 he tells us. The process of constructing a theory from such “free inventions” is described by Rudolf Carnap in these words: “The calculus is first constructed floating in the air, so to speak; the construction begins at the top and then adds lower and lower levels. Finally by the semantical rules, the lowest level is anchored at the solid ground of the observable facts.” Philipp Frank, who quotes the foregoing passage in a discussion of Einstein’s methods, goes on to say, “This conception of logical empiricism seems to be fairly in accordance with the way Einstein anchored his theory of gravitation in the solid grounds of observable facts by deriving phenomena like the redshift of spectral lines, etc.”107
The most appropriate comment that can be made on this statement is to repeat the previously quoted up-to-date opinion as to the true status of the gravitational red shift: “the red shift follows from more elementary considerations and is not really a test of general relativity.”56 In other words, the “solid grounds of observable facts” have turned out to be quicksand.
The fatal weakness in Einstein’s concept of deriving the basic laws of physics by “free inventions of the human mind” is that this policy makes no provision for correcting any errors in the premises, which are accepted as the foundation for the inventions. In essence this puts the scientific investigator in the same position as a mechanical computer. He can accomplish only those results, which are obtainable by manipulation of the data that are put into the system in the original program; if those data are erroneous then the answers that are obtained are necessarily wrong. The validity of the Special Theory of Relativity was programmed into Einstein’s mental analogue of the mechanical computer. His development of General Relativity and his attempt at development of a general field theory were therefore limited to what could be done by building on the Special Theory. Had that theory been conceptually correct, rather than merely a device, which attained mathematical validity by counterbalancing, one conceptual error with another, this procedure might well have been successful. But the usual reason for the protracted existence of a difficult physical problem is, as in this case, an error in the premises on which the theoretical reasoning is based, and Einstein’s methods were unable to cope with such a situation. He could only take refuge in what Margenau describes as making the theory more “abstract”: a term, which Einstein himself admits, is synonymous with making it more vague.
The possibility that errors in the basic premises of physical theory can be found and corrected by “free inventions of the human mind” is quite remote. Any program such as Einstein’s which relies on more and more abstraction definitely excludes any such possibility, since the need for any correction becomes progressively less apparent as the development of theory makes the conceptual structure progressively more vague. Some other purely speculative program might be better adapted to the purpose, but any procedure of this kind encounters almost insuperable obstacles. Innate resistance to altering long-established habits of thought, both on the part of the investigator himself and on the part of those who evaluate his work, is a powerful factor in this connection, but a still more formidable obstacle is the sheer inability of the human mind to devise conceptual innovations of the necessary scope, and magnitude without some outside help, such as is obtained by inductive processes from the data of observation and measurement.
The explanation of gravitation outlined in this work is a case in point. For hundreds of years the scientific world has accepted without question the contention that there are only two possibilities here: either we must admit the existence of action at a distance or we must admit that the effect is propagated through something with the properties of a medium (ether, field or deformable space). There is no reason to believe that the “free inventions of the human mind” would have produced any other possible explanation for many more hundreds of years; the scientific mind was already convinced that it had thoroughly explored the field. But the appeal to experience, which Einstein spurns as a “fictitious” basis for theory, has forced recognition of a third alternative, and when we are finally compelled by the weight of factual evidence to acknowledge that this alternative exists, it immediately becomes apparent that this new concept not only explains the existence of gravitation in readily understandable terms, but also explains all of the peculiar characteristics of the gravitational phenomenon with which other theories have had such a struggle.
This is by no means an isolated case. On the contrary, the great majority of our basic physical laws were “abstracted or deduced from experience” and were not “free inventions.” Whether or not the story of the falling apple is apocryphal, there is no question but that Newton’s Laws were distilled from experience. The same is true of the first step, which Einstein took along the relativity route. His Special Theory was not a “free invention”; it was deliberately designed to give a theoretical basis to a fact of experience: a mathematical relation—the Lorentz transformation—which expressed the modification of numerical values necessary to reconcile another fact of experience—the constant velocity of light—with the accepted laws of motion. According to the findings of this present work, the Special Theory was not a correct derivation from experiences (other than in its mathematical content) but it is definitely a derivation, not a free invention. The experimental facts were not relegated to the “fictitious” category by the theorists until after the shortcomings of the Special Theory manifested themselves by preventing a direct extension of the relationships of this theory to the more general situation of non-uniform motion.
It thus becomes evident that the difficulties which have led to Margenau’s conclusion that a fully satisfactory physical theory is impossible and that we must necessarily be content with something less than the optimum are not inherent in the structure of nature itself, but are a result of the fact that Einstein took the wrong road after his initial success and carried the scientific world with him. His argument in favor of the conclusion stated by Margenau cannot stand up under a cold-blooded scrutiny. The mere fact that two different theories, or many different theories, for that matter, achieve “a large measure of agreement with experience” does not preclude the existence of another theory, which agrees with all experience. Indeed, it raises a strong presumption that such a theory does exist. As Reichenbach puts it, “…contradictory theories can be helpful only because there exists, though unknown at that time, a better theory which comprehends all observational data and is free from contradictions.”108
The guideposts that have been set up in the preceding pages point out the true route the traditional scientific goal of a complete and understandable physical theory: a route which is almost diametrically opposite to the path toward increased flexibility (or abstraction) that has been followed by Einstein in the realm of the very large and by Bohr, Heisenberg and their associates in the realm of the very small. This opposite route is the one that has been taken in the development of the Reciprocal System. In this development Einstein’s dictum that we can only grasp “physical reality by speculative means” has been explicitly repudiated and the entire project has been devoted to accomplishing the very thing that Einstein claims is “doomed to failure”; that is, to “derive the basic concepts” of physical science “from the ultimate data of experience.”
The program that was followed in this work began with long years of study of the experimental values of the physical properties of thousands of different substances, directed toward the development of more accurate and more generally applicable mathematical expressions to represent the variability of these properties. After a number of such expressions had been formulated, the next step, one which also extended over many years, was an intensive study of these expressions, during the course of which they were thrown into every conceivable mathematical form, and each of the functions thus derived was subjected to an exhaustive examination in an attempt to discover possible physical relationships corresponding to the mathematical relations. Several of these lines of approach finally converged to the reciprocal postulate, bringing the inductive phase of the project to a conclusion. After the reciprocal postulate was formulated as the final product of this long and involved investigation of physical relationships, it became clear that this same conclusion could have been reached by a direct extrapolation of known facts, as indicated in the introduction to Part Three. However, the conceptual innovation that is required in order to make this extrapolation possible represents such a radical break with preexisting thought that it is difficult to take the necessary mental step, and the reciprocal idea did not actually crystallize until it became practically a matter of mathematical necessity.
The second, or deductive phase of the project initially involved the formulation of the collateral and supplementary assumptions required in conjunction with the reciprocal postulate to form the fully integrated set of postulates that underlies the Reciprocal System. The development of the consequences of the postulates of this system then followed. This is a gigantic task which is still under way and can be expected to continue for a long time to come, gradually extending into more and more detail. As can be seen from the foregoing description, the Fundamental Postulates of the Reciprocal System were obtained inductively from the empirical data, and all of the subsequent conclusions have been derived deductively from these postulates. This entire system therefore rests upon the facts of observation; it has been “derived from the ultimate data of experience.”
The final result of attacking the problem along this line has been the achievement of the very thing that current scientific thought assumes is unattainable: a complete and comprehensive theoretical structure that is readily understandable in the terms of reference of everyday experience. The present discussion covers only one of the many aspects of the Reciprocal System, but in each of the other subsidiary areas the same result has been obtained; that is, a development of the consequences of the Fundamental Postulates of this system has established a complete and logical theory for the phenomena included in the particular area: one which requires no supplemental theories or ad hoc assumptions, yet is consistent with all established knowledge throughout the field to which it applies.
XXIII
In retrospect it is clear that overconfidence in the capabilities of the theorists and in the validity of accepted modes of scientific thought has been a major factor—perhaps the most important factor—in diverting physical science from the straightforward path and into unproductive side excursions. Over and over again we find that a proposition which in reality is true only if the basic premises are valid and if no unrecognized alternative exists is accepted as a matter of logical necessity, and not infrequently is accorded a standing superior to that of the facts of observation.
The current viewpoint with respect to the propagation of the gravitational effect is typical. Modern physicists have been able to visualize only two alternatives: propagation at a finite velocity through a medium or instantaneous action at a distance. Being unwilling to accept action at a distance and thoroughly convinced that their inability to conceive of any other alternative is definite proof that no such alternative exists, they have taken it for granted that the effect must be propagated through a medium at a finite velocity, even though there is not the slightest evidence to support this conclusion, whereas there is some significant evidence to the contrary, including the inescapable fact that energy which is determined by position in space cannot be propagated through space.
Newton did not agree with the present-day viewpoint. He was equally as opposed to accepting action at a distance as the modern scientist, but he contended that the existence of gravitational effects conforming to his gravitational equation should be accepted as an empirical fact pending the discovery of some plausible explanation of the phenomenon at some future time. The developments of this work have completely vindicated Newton’s position. So far as this point is concerned, any judgment that may be passed on the merits of the present work is entirely immaterial. Whether or not the gravitational mechanism derived from the postulates of the Reciprocal System is ultimately accepted as correct by the scientific community, it cannot be denied that this does provide a third and totally different alternative in this case where present-day thought contends that no more than two alternatives are logically possible. The mere existence of this additional possibility is sufficient in itself to completely demolish the present contention that there are only two alternatives. We now know that there are at least three alternatives, and the fate of the confident assertion that only two alternatives exist should make it clear that any limitation of this kind is unsound. The contention that the possible alternatives in a case of this kind are confined to those already visualized assumes an omniscience on the part of the scientific profession, which the record certainly does not justify.
The situation with respect to the assumed contraction of objects in motion is similar. The statements that are made in this connection by modern authors are positive and categorical. “But the constancy of c in different inertial systems,” says Margenau, “requires that moving objects contract, that moving clocks be retarded, that there can be no universal simultaneity, and so forth.”109 Einstein is equally positive: “…if the velocity of light is the same in all CS (coordinate systems), then moving rods must change their length, moving clocks must change their rhythm… it is difficult to get rid of deep-rooted prejudices, but there is no other way.”110
Whatever someone else may think about the work of modern physical theorists, they have mode than ample confidence in their own results. There is no other way is about as definite and unequivocal as any statement can be. But it is now evident that it is totally wrong. There is another way; perhaps there may even be many other ways. Here again it is immaterial whether or not the new explanation presented in this work is accepted as correct. Whether correct or incorrect, the new theory derived from the Reciprocal System provides a logical and self-consistent explanation in which a constant velocity of light in all systems of reference does not require contraction of moving objects or retardation of clocks, and it thus automatically destroys all of the arguments that have been so confidently advanced by Einstein and his disciples on the basis of their assumption that “there is no other way.”
It is not appropriate to enter into an extended consideration of this aspect of modern science in a volume addressed to such a limited subject as gravitation, but one can hardly refrain from making some comment about the way in which the most astounding and fantastic conclusions are accepted by the scientific community purely on the basis of what amounts to an assumption that the collective opinion and judgment of the scientific profession are infallible. One of the standard tools of logic is the reductio ad absurdum in, which the falsity of certain assumed premises is proved by showing that the necessary and unavoidable consequences of these premises lead to an absurdity. But modern physical science now repudiates this well established doctrine and advances the weird contention that the basic premises which have been accepted by the scientific profession cannot be wrong, and hence the conclusions drawn from these premises must be correct, even if they are absurdities or near absurdities. It then follows as a matter of course that the universe itself is an absurdity. Here the physicist at least demonstrates that he has the courage of his convictions, for he does not shrink from this astounding end product of his line of reasoning. “The ‘real’ world is not only unknown and unknowable,” says Herbert Dingle, “but inconceivable—that is to say, contradictory or absurd.”111 Willem de Sitter argues that this conclusion, preposterous as it may seem, is in reality quite plausible: “After all the ‘universe’ is an hypothesis, like the atom, and must be allowed the freedom to have properties and to do things which would be contradictory and impossible for a finite material structure.”112 Even Bridgman, usually very much on the alert for fallacies of this kind, was swept along with the tide, and we find him making the flat statement: “The world is not intrinsically reasonable or understandable… ”113
Now let us bear in mind that no one is arguing that an absurd and contradictory universe is a priori more probable than a reasonable and rational one; the absurdity currently ascribed to the universe is simply a conclusion reached by developing the consequences of the initial premises from which the physicist starts his reasoning. On this basis, then, we would naturally expect that these initial premises would be of such a positive and incontestable character that there could be no reasonable doubt of their validity. But the truth is that the essential elements of these basic premises are almost invariably pure assumptions without factual support of any kind. As has been brought out in the preceding pages, the initial premises on which gravitational theory has been erected have reference to the properties of space and time, and these are the items, which Tolman says we simply “assume without examination.” The mere thought of trying to define the nature of time appalls him. Even philosophy, he says, would shrink from the task. Yet he has such overwhelming confidence in the validity of these unanalyzable basic assumptions, in spite of their dubious ancestry, that he is willing to accept the conclusion that the world is irrational and absurd rather than to concede that the initial assumptions are in any way open to question.
What has just been said with reference to Tolman and gravitational theory applies with equal force to the scientific profession as a whole and to physical theory in general. For example, the situation with respect to atomic theory which was discussed in detail in The Case Against the Nuclear Atom114 is a duplicate of the gravitational situation on a larger scale. Here again the basic premises are purely assumptions—even less than pure assumptions, we might well say, since some of them can only be justified by making the highly questionable additional assumption that existing knowledge about such matters does not apply in these particular cases—yet when these initial premises lead to absurdities, the physicist cheerfully concludes that the universe is inherently absurd and even denies the “objective reality” of the ultimate units of that universe rather than permit any shadow of doubt to be cast upon the sacrosanct assumptions on which the whole structure of currently accepted theory is based. Here is the true reason for the recurring “crises” with which modern physics finds itself faced: a situation which an outside observer, Jose Ferrater Mora, describes in these words, “Since approximately 1900 physics has been in what it is now customary to call ‘a state of crisis.’ No sooner has a theory been erected than its very foundations have started collapsing; new theories have been hastily introduced to patch up the shaky foundations only to have the same fate overtake them shortly.”115
Of course, a question such as that of the basic nature of time is not something that we can resolve by direct observation, and we have no option but to make an assumption of some kind. The fact remains, however, that when a development of the consequences of this and other basic assumptions ultimately leads to an absurdity, what we have proved is that one or more of the initial assumptions was in error, not that the universe is absurd and illogical. In arriving at the latter conclusion, the modern physicist is himself being absurd and illogical. It is quite evident that the “self-criticism” upon which physical science has relied to keep its progress headed in the right direction has failed in its appointed task, and that some more detached and less sympathetic analyses and appraisals of present-day physical theory are badly needed. As James R. Newman expresses it, the modern physicist has been allowed to “get away with murder,” and the consequences that have ensued make it clear that it is now high time that this unlimited license be revoked. No amount of sophistry or doubletalk can evade the cold, hard fact that the conclusions of modern physics as to the irrational and unpredictable behavior of the universe or portions thereof are nothing more than speculations; they are based on pure assumptions, not on solid knowledge.
Actually the theoretical physicists themselves are somewhat uneasy about the tenability of the position which they now occupy in this connection. The concept of a universe, which is basically irrational and absurd, is definitely objectionable from a philosophical standpoint, and considerable thought has therefore been applied to devising some modifications of this idea, which the scientist can live with more comfortably. Thus Herbert Dingle gives us a “new estimate” of the situation that differs materially from the uncompromising viewpoint which he expressed in the statement previously quoted:
The practice of physics has not changed, and the new estimate of its discoveries is forced on it; it is not a matter of choice. When we thought we were studying an external world our data were still simply our observations; the world was an inference from them. Until this century it was possible to make such an inference intelligibly… But now we find that… we can no longer express them as the structure of an external world unless we accept a world which is arbitrary, irrational and largely unknowable.116
In this statement Dingle has shifted his position and he now attributes the irrationality and unintelligibility not to the universe itself but to the limitations inherent in our observations: limitations which, he contends, make it impossible to deal directly with the universe itself. Here is a strange new idea totally foreign to the traditional philosophy of science. From the very beginning of scientific inquiry the great majority of scientists have agreed that the subject of their investigations is a physical universe external to and independent of the observer. But now Dingle and those who share this same viewpoint are repudiating this long-standing concept of the fundamental nature of scientific knowledge and are taking the stand that science is merely “a method of correlating sense-data.”
”On this view of science,” McVittie explains, “the Laws of Nature are simply the fundamental postulates lying at the base of a theory and are to be regarded as free creations of the human mind… Unobservable such as light, atoms, electromagnetic and gravitational fields, etc., are not constituents of an independently existing rational External World; are but concepts useful in the manufacture of the systems of correlation.”57 Heisenberg concurs: “…the new mathematical formulae no longer describe nature itself but our knowledge of nature.”117 Jeans expresses essentially the same thing: “The true object of scientific study can never be the realities of nature, but only our own observations on nature.”118
Now let us ask, what justification does modern science advance for this drastic revision of its basic philosophy? By any logical standards we are certainly entitled to be given some compelling reason for any such far-reaching change: some outstanding new discovery, perhaps, or some significant clarification of the general scientific picture. But do we get anything of this kind? Positively not. The whole case for this extraordinary alteration of the underlying philosophy of science rests on the assumption that the failure of the scientific profession to attain the goals originally envisioned cannot be due to any shortcomings on their part; it must be due to the fact that these goals are non-existent.
”In short,” says McVittie, “if the doctrine of a rational External World is accepted, past experience forces us to conclude that science is everlastingly in error, a Kepler, a Newton or an Einstein periodically ‘proving’ that his predecessors severe mistaken.”57 Most laymen would probably be willing to accept this as an eminently reasonable appraisal of the situation, aside from a certain amount of poetic license in the use of the word “everlastingly.” To them the idea that some future Smith, Brown and Robinson may continue the pattern of successive modifications of basic physical theory carried out by Kepler, Newton and Einstein is by no means inconceivable, nor does this, in their estimation, preclude the possibility that this process may ultimately culminate in a complete and fully satisfactory theoretical system. But the modern theorist will not concur in any viewpoint, which suggests that there is anything lacking in his own treatment of the problems. So far as he is concerned, what modern science has not been able to do cannot be done; where the objectives that have been established have not been reached the fault must lie in the problem, not in his methods of attack. To McVittie any inference that “science is everlastingly in error” is unthinkable, hence he regards the point brought out in the foregoing quotation as strong evidence of the falsity of “the doctrine of a rational External World,” even though to the ordinary observer there is no merit at all in this argument.
Dingle applies a similar type of reasoning in this statement: “…both relativity and quantum theory, the highlights of modern physics, are concerned not with an external world but with the operations of physicists and… they become nonsensical when they are presented as descriptions of external Nature.” If what Dingle asserts is true, then the most natural and logical conclusion is that these two “highlights of modern physics” are, in fact, nonsensical. But the present-day physicist refuses to recognize the possibility that the accepted pattern of thought of his profession may be wrong; he closes his eyes to this distressing prospect and pretends that it does not exist, thereby twisting Dingle’s point into another argument against the existence of a rational external world.
Once a more realistic appraisal of the situation is made and it is realized that it is no longer possible to avoid conceding that modern science could be wrong in its assumption of omniscience; that it could have overlooked some alternative explanations of the results of crucial experiments such as Rutherford’s scattering experiments and the Michelson-Morley experiment; that the presumed necessity of choosing between action at a distance and propagation through a medium (or the equivalent of a medium) is a result of insufficient consideration of the problem and not a reflection of the true physical situation, and so on, all such arguments against the existence of a rational external world independent of the observer simply collapse.
The new gravitational theory based on the postulates of the Reciprocal System sacrifices neither traditional logic nor the external world. Here again, as in the more specific situations previously discussed, this new theory adheres to the simple and natural viewpoint rather than introducing complicated and questionable ad hoc constructions. Just as the geometry of this system follows the familiar Euclidean pattern, physical magnitudes are fixed and unchanging, space is space, not a renamed ether, the gravitational effect is instantaneous just as our calculations have always assumed, Newton’s gravitational equation is universally valid, and so on, we also find that the gravitational effect which is revealed by our observations actually takes place in a rational external world of physical reality.
XXIV
Another feature of current scientific thought, which has been emphasized by the development of the Reciprocal System, is a strange dichotomy in the prevailing viewpoint concerning the nature of scientific proof. On the one hand, the possibility of the verification of a theory is specifically and categorically denied. Northrop tells us, for instance, “Thus no theory in mathematical physics can be established as true for all time. Nor can the probability of the truth of any given theory be scientifically formulated. For there is neither an empirical frequency nor a theoretical a priori definition of all the possibles with respect to which any particular theory can function as a certain ratio in which the number of all the possibles is the denominator term.”120 George R. Harrison goes a step farther and contends that we not only cannot prove that a theory is true, but that there is no such thing as an absolute truth. As he puts it, “…in recent years scientists have discovered, largely through such verified theories as Einstein’s Relativity, that our feeling that there is such a thing as absolute reality is incorrect, and that truth is always relative.”121
Similar statements are quite common in present-day scientific literature, but Harrison’s words are particularly interesting because he lets the cat out of the bag, so to speak, by telling us specifically where this remarkable conclusion comes from. Modern scientists have “discovered” that there is no absolute truth by means of a chain of reasoning based on the assumption that the Theory of Relativity is absolutely true. The extraordinary nature of this reasoning is still further emphasized by the extremely liberal standards that have been applied in arriving at the “truth” of the Relativity Theory. Here is a theory whose factual supports are so flimsy that, as Bondi says in the statement quoted in Part One, a “substantial minority” of present-day theoretical physicists regard them as wholly inadequate, yet this theory is accepted as a solid foundation on which to base conclusions of the most far-reaching character.
It cannot be denied that establishing the truth of a physical principle or theory is a difficult task. This fact has already been emphasized in connection with the discussion of the Relativity Theory in Part Four. This does not mean, however, that it is an impossible task, as Einstein and his disciples contend. As pointed out in the previous discussion, a theory can be proved if a correlation can be established between the theory and the facts of observation which is sufficiently complete and comprehensive to reduce the possibility of a hidden conflict somewhere in the system to a negligible level. This means that there must be an exact correspondence in a large number of cases throughout the area affected, without any inconsistency at any point, and without the use of contrived methods of evading contradictions or inconsistencies.
There is, of course, no definite rule by which we can say specifically at what point the probability of a hidden error becomes negligible; this will always be a matter of judgment. It is evident, however, that where a very large number of correlations are made and these correlations cover the entire field of application of the theory, so that the possibility of an unrecognized limitation on the scope of the theory is ruled out, there must be such a point somewhere along the line. Northrop’s contention that wee cannot arrive at the probability of the truth of a theory is thus manifestly erroneous in application to a theory which meets the requirements specified in the preceding paragraph. Here the “empirical frequency” and “definition of all the possibles” of which he speaks lose their meaning because the actual numerical values of the probabilities are no longer significant. After the term x in the function 1/x becomes so large that the difference between 1/x and zero is negligible, the exact value of x ceases to mean anything at all. No matter how much larger the term x may become, the effective value of 1/x still remains the same: it is still zero.
The present-day contention that positive proof is impossible in principle is therefore untenable; the most that can be asserted on any reasonable basis is that a rigid proof is not possible as a practical matter, and even here the facts do not support such a contention. It is true that most of the highly publicized physical theories of the current era, those which are so widely hailed as having revolutionized our entire scientific outlook, cannot be factually substantiated, since they are not only deficient in the number of correlations with observation and measurement, but are also inherently incapable of proof because they are based in part on principles of impotence. But oddly enough, the prevailing conclusions as to scientific proof in general are not applied here; in current practice these cherished products of modern ingenuity are accorded a status which puts them beyond the necessity of proof: a status which even qualifies them as basic principles that can be used to “prove” the validity of other conclusions, in the manner of Harrison’s contentions. The amazing extent to which this strange exaltation of currently popular theory has been carried is well demonstrated by the fact that no less a scientist than Sir Arthur Eddington begins one of his explanations with the statement, “One proof rests on Einstein’s theory.”122
Obviously there is much confusion in current thinking on this subject. With all due respect to Eddington, Harrison, and the many others, who have said essentially the same thing, a theory cannot be used to prove anything. We can prove the validity of a theory, in which case it becomes more than a theory, but as long as it is merely a theory and no more, it is, by definition, unproved and cannot be used to prove anything else. On the other hand, the extreme idea that nothing can be proved, an idea which, strangely enough, has been derived from considerations based on these popular theories whose validity is assumed without proof, is equally lacking in merit. Most of the broad general principles of physical science are still open to question in some degree, but there are a great many subsidiary laws and principles which meet every requirement for proof on the basic premise that proof has been attained when it has been demonstrated that the probability of error is negligible.
The case for the gravitational theory presented herein, and for the entire Reciprocal System of which the gravitational theory is a part, is based on this same concept of the nature of proof; that is, we have achieved a proof when we have reduced the chance of error to the vanishing point. In elaborating, it will be convenient to draw an analogy between scientific theory, which is a concise representation of scientific knowledge, and a map, which is a concise representation of geographic knowledge. The traditional method of map making involves first a series of explorations, then a critical evaluation of the reports submitted by the explorers, and finally the construction of the map on the basis of those reports which the geographers consider correct. Similarly in the scientific field explorations are carried out by experiment and observation, reports of the findings and the conclusions based on these findings are submitted, these reports are evaluated by the scientific community and those which are judged to be authentic are added to the scientific map: the accepted body of factual and theoretical knowledge.
But this traditional method of map making is not the only way in which a geographic map can be prepared. We may, for instance, devise some photographic system whereby we can secure a representation of an entire area in one operation by a single process. In either case, whether we are offered a map of the traditional kind or a photographic map we will want to make some tests to satisfy ourselves that the map is accurate before we use it for our purposes, but because of the difference in the manner in which the maps were produced the nature of these tests will be altogether different in the two cases. In checking a map of the traditional type we have no option but to verify each feature of the map individually, because aside from a relatively small amount of interrelation each feature is independent. Verification of the position shown for a mountain in one part of the map does not in any way guarantee the accuracy of the position shown for a river in another part of the map. The only way in which the position of the river can be verified is to compare what we see on the map with such other information as may be available concerning the river itself. Since these collateral data are often scanty or even entirely lacking, particularly along the frontiers of knowledge, the verification of a map of this kind in either the geographic field or the scientific field is primarily a matter of judgment and the final conclusion cannot be more than tentative at best.
In the case of a photographic map, on the other hand, each test that is made is a test of the validity of the process and any verification of an individual feature is merely incidental. If there is even one place where an item that can definitely be seen on the map is in conflict with something that is positively known to be a fact, this is enough to show that the process is not accurate and it provides sufficient justification for discarding the map in its entirety. If no such conflict is found, however, the fact that every test is a test of the process means that each additional test that is made without finding a discrepancy reduces the mathematical probability that any conflict exists anywhere on the map. By making a suitably large number and variety of such tests the remaining uncertainty can be reduced to the point where it is negligible, thereby definitely establishing the accuracy of the map as a whole. In making these tests it is neither necessary nor advantageous to give any consideration to items which are in any degree doubtful. It serves no purpose because there is nothing to be gained by establishing the existence of a conflict if the significance of that conflict is unknown. It is not necessary because a map of this kind includes so many hundreds or thousands of individual features that there are ample opportunities for comparisons with facts that are not open to question, even if some areas are inaccessible. The whole operation of verifying a map of this kind is therefore a purely objective process in which features that can definitely be seen on the map are compared with facts that have been definitely established by other means. The final conclusion is an unequivocal yes or no.
This is the kind of a map of the scientific field which is presented in The Structure of the Physical Universe and the more detailed discussion of the gravitational aspects of the Reciprocal System in this volume. Like the photographic map, the theoretical structure developed in this work has been produced in one operation by a single process and it is therefore subject to the same kind of positive verification. The entire work consists of the development of the consequences of two fundamental postulates without the introduction of any other factors of any kind. If the postulates are valid then certain primary consequences, including the existence of radiation, gravitating matter, electric and magnetic effects, and the other major physical phenomena, necessarily and unavoidably follow. Interaction of these primary consequences with each other and with the postulates then results in a large number and variety of secondary consequences, and further development along the same lines ultimately produces a system, which is so extensive that it constitutes a complete theoretical universe. Having been developed entirely by the application of mathematical and logical processes to the fundamental postulates, this whole system is one integral unit. If the postulates are valid then each and every one of the necessary consequences is likewise valid. Conversely, if even a single one of the thousands of these necessary consequences conflicts with a fact that has been definitely established, the postulates are thereby invalidated and the entire structure falls. But if no such conflict is found in making a very large number of comparisons with known facts the probability of the existence of any hidden conflict anywhere in the system is reduced to a negligible level. Thus the verification of this theoretical system, like the verification of the photographic map, is a purely objective process in which there is no place for judgment or opinion.
There is, however, one important precaution, which must be observed: we must be certain of the validity of the alleged facts, which we propose to use for test purposes. As has been emphasized previously, the human mind is so constituted that it does not like to admit ignorance and in those cases where we do not know there is a rather strong tendency to dress our best guess in fine clothes and parade it as knowledge. For example, one of the first items to emerge from the new theoretical development is a new concept of the structure of the atom, and the general opinion undoubtedly will be that this conflicts with a known fact: the nuclear atom. But in reality we do not know that the atom has a nuclear structure. On the contrary, the facts brought out in The Case Against the Nuclear Atom114 show that such a structure is impossible. Even during the time that it was universally accepted, the acceptance was not based on agreement between the theory and the facts of observation; it could be justified only by the assumption that the known facts do not apply in the atomic situation, either because there are some unknown forces which offset the known forces that would otherwise disrupt the hypothetical atomic structure or because the laws and principles that are valid in the known areas of the universe do not apply on the atomic scale.
Similarly the new development finds normal hydrogen (H1) more stable than helium under high temperature conditions, which rules out the conversion of hydrogen to helium as an available process for the generation of stellar energy. Here again the first reaction is likely to be that the new concept is in conflict with an established fact, but the hydrogen conversion process is not a known fact; it is actually nothing more than the best guess thus far, in spite of the virtual unanimity with which it is currently accepted. Certainly no one is able to prove that this is the process whereby energy is generated in the stars, nor can it be shown that it is a naturally occurring process anywhere. It has been demonstrated that the unstable isotopes of hydrogen can be stimulated in such a manner as to cause them to do rapidly what they will do spontaneously at a slow rate, and the stable hydrogen isotope can be altered forcibly (that is, by the expenditure of energy) but there is no evidence that this stable isotope can be caused to become unstable.
Development of the consequences of the fundamental postulates of this work results in many other conclusions which differ from currently accepted ideas but careful analysis has indicated that all of these cases are similar to those mentioned in the preceding paragraphs; that is, these popular ideas which are challenged by the new system are not factual; they are either inferences, hypotheses, or unsupported extensions of observational findings. In no case does this analysis disclose any conflict with genuine facts. Many of the theoretical conclusions cannot be tested at all, since they apply to areas in which no factual knowledge exists, but wherever and whenever the theory can be checked against solid facts the two are in agreement.
It is perhaps inevitable that such statements in favor of a new and revolutionary theory should be met with profound skepticism, but the objective of this discussion is to bring out the point that the appraisal of the new theoretical structure by the scientific community can be, and therefore should be, a purely objective check of theory against fact, without regard for the characteristically human but definitely unscientific sentimental bias in favor of familiar ideas. Nor should it be in any way surprising when this objective check does verify the validity of the new theory. After all, the most conservative assumption that we can make about the phenomena in the unknown regions of the universe, the assumption that has by far the greatest a priori probability of being correct, is that they follow the same relationships that hold good in the known regions. This work has, for the first time, explored the consequences of extrapolating all of the basic relations in the known regions, including the relationship between space and time, and in view of the high inherent probability that such an extrapolation will yield correct results, it should be no occasion for surprise or incredulity when the theoretical deductions based on these premises are found to be in full agreement with the facts.
