Chapter XXVII
Electric Current Properties
At this point it will be helpful to review the status of the various electrical quantities from the standpoint of their relationship to the basic entities, space and time. Electrical quantity, Q, has been identified as space, s, and current, I, has similarly been identified as velocity, s/t. Resistance, R, is defined in such a manner as to make it equal to mass per unit time, t3/s3 × 1/t = t2/s3. Electrical energy is interchangeable with energy in other forms and like energy in general is t/s, the reciprocal of velocity.
Energy per unit time is power, hence power is t/s × 1/t = 1/s. Power divided by current is electromotive force, which makes this quantity equal to 1/s × t/s = t/s2 . This is the general expression for force, and the electromotive force, F, IR, or emf, therefore has the same basic characteristics as other forces, gravitational, mechanical, etc. In many respects it is analogous to gas pressure, which is also a force phenomenon; that is, force per unit area. The magnitude of the emf, or potential, at any point may be increased in the same manner that gas pressure is increased, either by the introduction of more electrons of the same average velocity or by imparting a greater velocity to the electrons already present. If this location is connected by means of a conductor with a region which does not participate in the increase in potential, the force difference which is created will cause a flow of current from the high potential region to the region of lower potential. This flow will persist until the potentials are equalized. Ordinarily we deal with currents which are produced by some agency that creates a continuing potential difference, and the current flows in a circuit starting and terminating at the generating agency. It is not essential, however, that such a circuit exist; a current will flow between any two points of different potential if the necessary conductor is available.
When the potential difference which caused the flow of current is eliminated the directional movement of the electrons which constitutes the current ceases. The electrons remaining in any particular volume, however, continue to react with the moving atoms of matter and since the electrons as well as the atoms are free to move the eventual result is an equilibrium wherein the thermal motion is divided between motion of mass through space and motion of space (electrons) through matter. The nature of the equilibrium; that is, the division of motion between the electrons and the mass, is determined by the average resistance in all directions. At a given temperature the atoms of a low resistance conductor such as copper impart less velocity to the electrons than the atoms of a conductor such as iron which has a greater resistance. Under the same conditions the various conductors therefore have different electron velocities and where the density of electrons is the same the electron pressure or potential depends upon the characteristics of the conductor. It should be noted, however, that the resistance of a conductor to the thermal motion of the electrons is not necessarily identical with the resistance which this conductor offers to the flow of electric current, inasmuch as there is no requirement that the directions of these motions be coincident. The possibility of a difference in flow direction is obvious in the case of anisotropic substances but even where the conductor is isotropic the directions of movement relative to the line of action of the inter-atomic forces may not coincide.
If we place two conductors with different electron potentials, copper and zinc for example, in contact the higher potential of the electrons in the zinc will cause a flow from the zinc to the copper until the density of electrons in the copper becomes great enough to equalize the potential. We then have an equilibrium of potential between a smaller number of high velocity electrons in the zinc and a greater number of low velocity electrons in the copper. This difference in potential which becomes apparent when two dissimilar conductors are placed in contact is known as a contact potential.
The effect of temperature on any aggregate of electrons is more complex than the corresponding effect on an aggregate composed of material atoms. The latter exists in free space and consequently the reaction to addition or removal of thermal energy is determined by the properties of the material aggregate itself without any modification by the environment. The behavior of the electron aggregate, on the contrary, is determined not only by its own properties but also by the properties of the conductor in which it is located. As a result the electronic effects show a range of variation both in magnitude and direction which is totally foreign to the analogous phenomena involving material atoms.
If a conductor is heated, the primary effect on the electrons within the conductor is a decrease in potential, the reaction of the electrons (units of space) being the inverse of the reaction of the material atoms (units of time) to the same addition of energy. Simultaneously, however, the heating of the conductor causes an increase in resistance and a corresponding increase in the potential per electron, as explained in the preceding paragraphs. The net result depends on the relative magnitude of the two effects. In a low resistance conductor such as copper or silver, the increase in potential due to the heating of the conductor is smaller than the direct effect of the temperature on the electrons and there is a net loss in potential as the temperature rises. When a conductor of this type is heated at one end only the cold end acquires a higher (more negative) potential: a phenomenon known as the positive Thompson effect. In a conductor such as iron or mercury which has a higher resistance the increase in potential due to the change in resistance may be greater than the direct effect on the electrons, in which case the hot end of the conductor acquires the higher potential: the negative Thomson effect. The effective resistance for this purpose is, of course, the resistance to thermal motion of the electrons and it does not necessarily coincide with the resistance to directional flow, as previously pointed out, but there is a general qualitative correspondence between the two, as would be inferred from the examples cited.
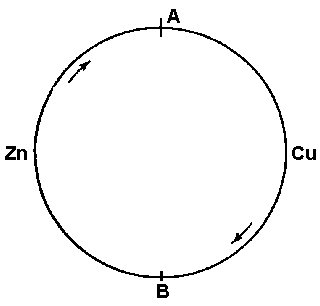
Figure 41
Now let us construct a circuit of two different conductors as in Figure 41 and cause a current to flow in this circuit. At junction A where the electrons flow from zinc to copper they leave the zinc with the relatively high potential which represents the equilibrium condition in the zinc conductor. In the copper conductor the equilibrium potential is lower, and the electrons therefore reduce their potential in the process of attaining equilibrium. This reduction in electrical potential corresponds to an increase in thermal energy and consequently the electrons absorb heat from the surroundings. The flow of electrons thus results in a cooling effect at junction A. Where the electrons return to the zinc conductor at junction B the reverse process takes place and heat is given up to the environment. This phenomenon is known as the Peltier effect.
The inverse of the Peltier effect is the Seebeck effect or thermoelectric effect. Here heat is applied to junction A. This lowers the potential per electron and since there are more electrons in the copper than in the zinc the effective potential of the copper drops below that of the zinc, causing a current flow from zinc to copper. If both junction A and junction B are at the same temperature the flow is only momentary until the necessary potential equilibrium is established but if one junction alone is heated a continuous current is produced and heat is transferred from the hot junction to the cold junction through the agency of the current.
In view of the free motion of the electrons in conductors and the establishment of thermal equilibrium between the electrons and matter it is obvious that the thermal energy will similarly tend to equalize in all parts of any system which is inter-connected electrically. It follows that the electron movement constitutes a means of heat transfer whenever a conductor is available. This type of heat transmission is called conduction.
It should be noted particularly that the motion of the electrons through matter is an integral part of the total thermal motion, not something separate. A mass m reaches a certain temperature T when the thermal velocity attains a specific average value v. It is immaterial from this standpoint whether the velocity consists entirely of motion of the mass through space or partly of such motion and partly of motion of space (electrons) through the mass. In either case the total velocity corresponding to the temperature T remains the same. In previous discussions of the theory that metallic conduction of heat is due to the movement of electrons the objection has been raised that there is no indication of any increase in the specific heat due to the thermal energy of the electron movement. The answer lies in the foregoing explanation that the thermal motion of the electrons is not an addition to the thermal motion of the atoms; it is an integral part of the atomic motion and hence has no effect on the specific heat.
Since the conduction of heat is accomplished through the same agency as the conduction of electric current—the movement of electrons—it follows that the resistance to the flow of heat is the same as the resistance to the flow of current. There is, however, a difference in the mechanism of conduction which introduces an additional factor into the heat flow. The force causing the flow of current is a directional force imposed from the outside and unaffected by the conditions within the conductor. The application of heat to one end of a conductor does not introduce any such directional force; it merely changes the average velocity of the electrons in the heated zone and the directional force gradient is a secondary effect. The greater the velocity gradient in the electron aggregate the more rapidly the velocity will be transferred, hence the effective force causing the heat flow is proportional to the temperature. The actual rate of heat transfer is the result of a combination of these two factors. As the temperature increases the resistance also increases, reducing the rate of heat flow. The same rise in temperature increases the rate of flow by reason of the greater thermal gradient. In the neighborhood of room temperature these two influences are nearly equal and the thermal conductivity, C, therefore has only a relatively small temperature variation. The general relation in this temperature range is expressed in approximate terms by the well-known Wiedemann-Franz Law:
| C = k T/R |
(120) |
For greater accuracy it is necessary to take the initial level into account in both the thermal and electrical factors. Expressing the resistance in terms of temperature and introducing the initial level in both cases, we have the revised equation:
| C = k (T-IT)/(T - IE) |
(121) |
At the higher temperatures where T is much larger than IT or IE, a variation in T has relatively little effect on C and equation 121 gives substantially the same results as the Wiedemann-Franz Law (equation 120). As the temperature decreases the difference between IT and IE becomes increasingly effective and since IE is normally larger than IT the value of C rises, slowly at first and then more rapidly. When T - IE approaches zero, however, the resistance diverges from the linear relation and follows a probability curve, as we have seen in our examination of the resistance relations. Beyond this point, therefore, further change in the denominator of the conductivity equation is relatively slow and the decrease in the numerator becomes the controlling factor. The thermal conductivity thus passes through a maximum and then drops gradually to zero at zero temperature. Here there is no resistance to the electron flow but nevertheless there is no heat conductivity because the electrons have no thermal motion.
The general shape of the experimental thermal conductivity curves agrees with the theoretical curve as described in the foregoing paragraph. In view of the uncertainties in the measurements at low temperatures, however, it has not appeared worth while to set up any detailed comparisons for this low temperature range, and since ample supporting data for the Wiedemann-Franz relation at the higher temperatures are available elsewhere, no heat conductivity comparisons are included in this presentation.
