Chapter XXXVI

The Galactic Cycle

Let us now turn to another of the major evolutionary problems: the galactic cycle. The use of the term “cycle” in this connection may seem to be putting the cart before the horse, since no evidence of any cyclic course of evolution has heretofore been recognized, but in a universe based on the Fundamental Postulates of this work a galactic cycle is mandatory. As brought out in the discussion of the permanence of the major features of the universe, half of this cycle is located in our material sector of the universe and the other half in the non-material sector.

The necessity for a means of interchange between the material and non-material sectors has already been pointed out. This, of course, involves the existence of some process whereby the rotational space displacements of the non-material universe can be converted into the rotational time displacements which we recognize as matter. The nature of this process will be discussed later, but it is evident that new matter or potential matter entering the material sector of the universe from the non-material sector as a result of such a process cannot have any preferential location in space, since the physical entities of the non-material sector are not localized in space. It will also be shown in the subsequent discussion that all of this new matter is produced in the form of individual atomic units. These newly produced atoms uniformly distributed throughout space come under the influence of gravitational forces as soon as they are formed and a process of aggregation begins. As one vast period of time follows another and gravitation continues its slow but unremitting action the aggregates grow larger, the atoms become particles, the particles become clouds, the clouds become stars, the stars gather in clusters, the clusters become galaxies, the galaxies become larger galaxies. In the meantime the space-time progression moves the galaxies outward away from each other in space and new aggregations form from new matter and remnants of the old in the areas left vacant by the larger units. In due course these new formations grow older and larger and follow in the paths of their predecessors, leaving new vacancies to be filled by still other aggregations originating in the same manner. Each generation has its period of development, comes to maturity, and finally reaches the point of reconversion into the non-material sector of the universe to start the second half of the cycle. In order to make certain that the basis for this theoretical picture is clear, let us look at the gravitational situation as defined by the Fundamental Postulates. Every location in the universe is moving outward from every other location at unit velocity because of the space-time progression resulting from the equivalence of the basic units of space and time. Simultaneously all material atoms are moving in the opposite direction, inward toward each other, because of their rotational motion. At the shorter distances the inward motion exceeds the outward motion and the atoms move closer together. As the distance increases, however, the rotational motion toward any specific location decreases according to the inverse square relation and at extreme distances the gravitational motion is reduced to the point where it is less than the oppositely-directed velocity of the space-time progression. Beyond the point of equality the net resultant motion is outward, increasing toward unity (the velocity of light) as the distance increases.

These motions control the large-scale aspects of the material universe. Within the range of effectiveness of the gravitational motion, or gravitational forces, if we wish to speak in terms of the force equivalent of the motion, all units of matter move inward toward each other and if given sufficient time must join. Various subsidiary motions may control the nature of the combinations; for instance, they may cause orbital motion rather than actual consolidation, but they cannot prevent combination other than temporarily. Within the effective gravitational range, therefore, the aggregates of matter are continually growing. At the same time the space-time progression is increasing the separation between each of these aggregates and all others which are beyond the gravitational limit. The net effect is therefore a process of aggregation and a separation of the aggregates: formation of galaxies and expansion of the universe, to use the familiar terminology.

Once more, as in the discussion of the stellar cycle, let us see how close an agreement we can find between the purely theoretical course of evolution, as derived from the Fundamental Postulates and described in the foregoing paragraphs, and the results of astronomical observations. Since we are postponing consideration of the transitions to and from the non-material sector of the universe, the question now confronting us is whether we can recognize a definite course of evolution in the galaxies and pre-galactic structures from diffuse matter to a final form of some kind.

According to the theoretical evolutionary outline which has been presented, the primary criterion of age in the galactic world is size. It must be realized, of course, that accidents of environment and other factors will affect this situation to some extent so that the principle does not necessarily apply in every individual case, but in general the ages of the various types of structures theoretically stand in the same order as their sizes. Turning from theory to observation, we find that the recognized giants among the galaxies are the spirals. There is, in fact, a rather definite lower limit below which the spiral structure does not appear at all. The other major class, the elliptical galaxies, is found all the way down to the limits imposed by the capabilities of the observational equipment but is not represented above the lower limit of the spirals, except by certain very large systems which have the shape of elliptical galaxies but are much different in other respects. The criterion of size therefore definitely places the elliptical galaxies as the younger type and the spirals as the older, as in Hubble’s original classification. It also follows on the basis of this criterion that small spirals are in general younger than larger spirals and small aggregations of the elliptical type are younger than larger elliptical galaxies.

Now let us ask what evolutionary sequence would be normal for matter subjected to the forces which exist in the galaxies. There has been a great deal of speculation as to the nature of the forces responsible for the spiral form, but the justification for such speculation is rather questionable in view of the fact that the forces which are definitely known to exist, the rotation and the gravitational attraction, are sufficient in themselves to account for the observed structure. Inasmuch as the individual units in the galaxy are independent and widely separated the aggregate has the general characteristics of a fluid. A spiral structure in a rotating fluid is not unusual; on the contrary a striated or laminar structure is almost always found in a rapidly moving heterogeneous fluid, whether the motion is rotational or translational. It is true that objections have been raised to this “coffee cup” explanation on the grounds that the spiral in the coffee cup is not an exact replica of the galactic spiral, but it must be remembered that the coffee cup lacks one of the forces that plays an important part in the galaxy: the gravitational attraction toward the center of mass. If the experiment is performed in such a manner that a force simulating gravity is introduced, say for instance by replacing the coffee cup by a bowl which has an outlet at the bottom center, the resulting structure on the surface of the water is practically a picture of the galactic spiral.

In this kind of rotational structure the spiral is the last stage, not an intermediate form. By proper adjustment of the rotational velocity and the rate of water outflow the original dispersed material on the water surface can be caused to pull in toward the center and assume a circular or elliptic shape before developing into a spiral, but the elliptic structure precedes the spiral if it appears at all. The spiral is the end product. It will be brought out later in the discussion that the manner in which the growth of the galaxy takes place has a tendency to accentuate the spiral structure, but the rotating fluid experiment shows that the spiral will develop in any event when the necessary velocity is attained. Furthermore, this spiral is dynamically stable. We frequently find the galactic spirals characterized in astronomical literature as unstable and inherently short-lived, but the experimental spiral does not support this view. From all indications the spiral structure could persist indefinitely if the rotational velocity remained constant.

However, the rotational velocity of the galaxies does not remain constant. During the early stages of galactic aggregation when the combining units are of the same general order of magnitude, it is to be expected that some rotation will develop because of non-central impacts. Once such a rotation is initiated a difference in the rate of accretion develops between the two opposite sides of the galaxy in the plane of rotation. This accretion rate is affected very materially by the velocity of the mass relative to the diffuse material through which the galaxy is moving. On one side the net velocity is the sum of the translational and tangential velocities; on the other side it is the difference. The impact of the incoming particles or aggregates is therefore asymmetric and the result is an increase in rotational velocity with the age of the structure. Here again there are individual deviations, but in general the rotational velocity is directly related to the size and age of the galaxy and it is therefore one of the criteria of age.

Closely connected with the velocity is the shape of the rotating structure. The correlation in this case is so obvious that in actual practice the velocity is generally inferred from the shape rather than measured directly, although measurements have been made in some cases where conditions are favorable. Increased rotational velocity in the elliptical galaxies results’ in greater eccentricity. Beginning with the globular clusters, which are rotating very slowly and are spherical or nearly spherical, the elliptical units pass through all stages of eccentricity down to strongly lenticular shapes. At this point the spiral disk develops. The structure of the young spiral can be described as loose: the arms are thick and widely separated and the nucleus is rather inconspicuous. As the galaxy grows older and larger the nucleus becomes more prominent and the increased rotational velocity causes the arms to thin out and wind up more tightly. In the limiting condition the galaxy is practically all nucleus and the spiral arms are wound around this central mass so tightly that in effect they become part of it. These changes in appearance in the final stage account for some of the apparent deviations from the normal relation between size and age. There are a number of very large galaxies which are classified as elliptical, although they are greatly in excess of the size which normally results in the development of the spiral structure. The logical explanation is that these are not actually elliptical galaxies; they are the tightly wound, rapidly rotating, giant spirals which have reached the end of the road as galaxies and are ready to take the next step in the evolutionary cycle. Some particularly interesting inferences along this line can be drawn from the characteristics of the giant galaxy Messier 87, one of the well-known examples of this class, and this subject will receive further attention later.

At this point it may be appropriate to digress long enough to point out that if the correlation between size and shape is as close as is indicated by this preliminary examination of the theoretical relationships, it should have some useful applications in observational astronomy, particularly in the study of the more distant galaxies. Some complications are, of course, introduced by modifications of the basic structural pattern. The most common of these modifications, the barred spiral, will be given further consideration in another connection.

The fourth criterion of age applicable to the galaxies is that of relative abundance. In the evolutionary course as outlined, each unit of aggregation is growing at the expense of its environment. The smaller units are feeding on atoms or small particles, but the larger aggregations pull in not only the particles in the immediate vicinity but also any of the small aggregates which are within reach. As a result of this cannibalism the number of units of each kind should progressively decrease with age. When we examine the existing situation we find that the order of abundance is essentially in agreement with the age as determined by other criteria. The giant spirals, the senior members of the family of galaxies according to these criteria, are relatively rare, the smaller spirals are more common, the elliptical galaxies are abundant, and the globular clusters, which may be regarded as junior elliptical galaxies, exist in enormous numbers. It is true that the observed number of small elliptical galaxies, those in the range just above the globular clusters, is considerably lower than would be predicted from this sequence, but it is evident that this is a matter of observational selection. When the majority of galaxies are observed at such distances that only the spirals and the largest of the ellipticals are big enough to be visible it is not at all strange that the observed spirals are proportionately more numerous than is predicted by theory. The number of additional elliptical galaxies discovered within the Local Group in very recent years, increasing the already high ratio of elliptical to spiral in the region most accessible to observation, emphasizes the importance of this selection process.

A fifth criterion of galactic age is provided by the ages of the constituent stars. After a galaxy has reached the stage where the complete stellar cycle is represented the evaluation of galactic age becomes a matter of determining just how many times the constituent stars have been around the cycle: a somewhat complex problem. It is, however, relatively simple to distinguish between the galaxies which are old enough to have stars in all phases of the cycle and those in which the most advanced stars have not yet reached the upper portion of the main sequence, and this distinction is all that is required for present purposes. The initial product of condensation from the primitive material is, of course, identical with the product of condensation of a diffuse mass expelled from an exploding star; that is, it is a red giant. Under normal conditions this new star, irrespective of its origin, will follow one of the usual evolutionary paths: the lines AB or AD in Figure 42.

The smallest of the stellar aggregations in the line of galactic evolution, the globular clusters, are composed primarily of stars that are in the neighborhood of the initial evolutionary line AB. In some cases the line AD is also represented and frequently there are stars along the lower portions of the main sequence, but there are no representatives of the advanced types: the hot massive stars. We therefore conclude from this evidence that the globular clusters are relatively young structures, which agrees with the testimony from other sources. The next larger aggregates, the elliptical galaxies, are composed of stars of the same general type as those of the globular clusters, the so-called Population II. Here, however, a few blue giants are occasionally found—indications that the general age level is increasing. Then when we reach the spirals the full complement of advanced type (Population I) stars makes its appearance, confirming the status of these galaxies as the oldest inhabitants of the material system.

Another possible method of identifying the age of a galaxy or other material aggregate is a determination of the proportion of heavy elements in the matter of which it is composed. As indicated in the preceding discussion, the building up of heavy elements from the hydrogen and helium atoms which are the initial products in the formation of matter is a slow but continuous process. The elements heavier than the nickel-iron group are destroyed in the stellar cycle and it can be expected that the total amount of these elements will reach an equilibrium value and will not increase above this level, but the proportion of elements in the intermediate range should continue to increase indefinitely as the aggregate grows older. If the proportion of heavy elements in an aggregate can be measured, this measurement then serves as an indication of age. Obviously an accurate determination of this quantity presents some difficult problems, but some attempts in this direction have been made and it is interesting to note that the results of these initial efforts are entirely in accord with the ages of the various structures as inferred from other data. A recent evaluation finds the percentages of elements heavier than helium ranging from 0.3 in the globular clusters, theoretically the youngest stellar aggregation available, to 4.0 in the Population I stars and interstellar dust in the solar neighborhood, theoretically the oldest material within convenient observational range.

In the preceding paragraphs we have considered six different items which should theoretically serve as criteria of galactic age: (1) size, (2) rotational velocity, (3) shape, (4) relative abundance, (5) age of the constituent stars, and (6) proportion of heavy elements. All of these criteria are in agreement that the observed galaxies and sub-galaxies can be placed in a sequence which confirms the theoretical deduction that there is a definite evolutionary path in the material universe extending from dispersed atoms and sub-material particles through particles of matter, clouds of atoms and particles, stars, clusters of stars, elliptical galaxies and small spirals to the giant spiral galaxies which constitute the final stage of the material phase of the galactic cycle. It is possible, of course, that some of these units may have remained inactive from the evolutionary standpoint for long periods of time, perhaps because of a relative scarcity of galactic “food” in their particular regions of space, and such units may be chronologically older than some of the aggregations of a more advanced type. The capture of relatively large aggregates also necessarily results in a temporary divergence from the normal relationship between age and size. Such variations as these, however, are merely minor fluctuations in a well-defined evolutionary course.

Next we turn to a different kind of evidence which gives further support to the theoretical conclusions. In the preceding discussion it has been demonstrated that the deductions as to continual growth of the material aggregates by capture of matter from the surroundings are substantiated by the fact that the ages of the various types of galaxies, as indicated by several different criteria, are definitely correlated with their respective sizes. Now we will examine some direct evidence of captures of the kind required by theory. First we will consider evidence which indicates that certain captures are about to take place, then evidence of captures actually in progress, and finally evidence of captures that have taken place so recently that their traces are still visible.

The early history of the process of aggregation must be derived principally from theory since the observation of small non-luminous aggregates is possible only to a very limited extent (at least with the facilities now available). We deduce that the atoms which constitute the initial phase of matter combine to form particles, and this deduction is confirmed by evidence of the existence of dust particles in interstellar space. We further deduce that these particles gather together into dust clouds and that stars are formed from clouds of dust and gas when the first magnetic ionization level is reached and an adequate source of heat is thereby activated. At this point the aggregates become self-luminous and the task of the observer is greatly simplified, although the enormous distances which are involved still stand as formidable obstacles to complete knowledge. From the information gathered by observation two striking facts about the formation of the stars emerge. First, we find that the stars are separated by almost fantastic distances and that the most powerful gravitational forces in the universe, those in the central regions of the largest galaxies, are not able to reduce this separation by any significant amount. (From the standpoint of this discussion binary and multiple stars are regarded as stellar units, and the term “star” should be understood as including such systems.) The second of these rather surprising facts is that, although direct observation is possible only in very limited areas, we have sufficient observational information to show that single stars and relatively large groups (globular clusters) are abundant throughout space, but there is no indication of the existence of aggregations of intermediate size.

In order to throw some light on the situation which is responsible for these somewhat bizarre relationships, let us turn back to gravitational theory. We have found that the gravitational force exerted by mass m on unit mass at distance d is m/d². At the point where the gravitational force exerted on unit mass is unity in all effective dimensions the gravitational and space-time forces are likewise in equilibrium in all dimensions. We have previously evaluated the inter-regional ratio of effective dimensions as 156.44 and we have found that a total of 3 × (156.44)³ three-dimensional units in the time region are required to produce one effective unit parallel to the time-space region forces. The ratio of the total gravitational force to the force exerted against a single one-dimensional rotational unit is therefore

3 × (156.44)³ × 3 × 156.44 = 5.391×10⁹.

On this basis the equilibrium equation between the gravitational force and the unit force of the space-time progression is

1 / (5.391×109) × m/d02 = 1

(156)

Solving for d₀, we obtain

d0 = m½ / 73420

(157)

At this distance do the gravitational motion is equal to the space-time progression and there is no resultant motion in either direction. At distances less than d₀ there is a net inward velocity. Beyond do the net velocity is outward. We thus find that for any specific mass there is a gravitational limit beyond which the net effective force reverses direction and the resultant motion is outward rather than inward.

Here, then, is the explanation for both of the extraordinary characteristics of the stellar distribution. The stars are separated by tremendous distances because each star or pre-stellar cloud continually pulls in the material within its gravitational range and this prevents the accumulation of enough matter to form another star in this space. Formation of additional stars can take place only outside the gravitational limits and when such stars originate outside these limits they move outward from all previously existing stars. The immense region within the gravitational limit of each star is therefore reserved to that star alone.

The mass of the sun has been calculated as 2×10³³ g, which is equivalent to 1.205×10⁵⁷ natural units of mass. The corresponding number of natural units of space is the square root of this quantity or 3.47×10²⁸, which amounts to 1.58×10²³ cm or 167,000 light years. Applying the coefficient of equation 157 we find that the gravitational limit of the sun is at 2.27 light years. The nearest star system, Alpha Centauri, is 4.2 light years distant and the average separation of the stars in the vicinity of the sun is estimated at 2 parsecs or 6.5 light years. Sirius, the nearest star larger than the sun, has its gravitational limit at 3.5 light years and the sun, 8.7 light years away, is well outside this limit. It is evident that this space distribution in which the minimum distance is two-thirds of the average requires some kind of a barrier on the low side; it cannot be the result of pure chance. The existence of a gravitational limit just below the minimum stellar separation explains the highly abnormal distribution.

From the foregoing figures and the relation indicated by equation 157 it can also be seen why small clusters of stars are not formed under normal conditions. Let us consider, for example, a hypothetical cluster of ten stars in a region in which the stars of the general field are uniformly spaced at a density equal to that in the neighborhood of the sun. On calculating the gravitational limit of the cluster we find that even the closest of the field stars are outside this limit. Since the density of matter in the dust clouds from which the stars are formed is no greater and probably less than that assumed for purposes of this calculation, it is apparent that a cluster of this size not only could not grow but could not even be formed in the first place. We deduce, therefore, that where a large number of stars form contemporaneously from a dust cloud of vast proportions a relatively large star cluster is formed, but that all other stars are formed as individual units.

Within the clusters the star density is greater than that in regions such as the one in which the solar system is located, but the nature of the force equilibrium in any aggregation of stars is such as to preclude any major increase in the density. Unlike the units of matter within the star, each of which exerts a force of attraction on all others, the individual stellar units within the cluster repel each other and the cluster is held together only by the gravitational attraction between the individual stars and the cluster as a whole. This limits the concentration toward the center and, except for the outer regions in which the density gradually drops to the near zero value of the surrounding space, it is probable that the density is nearly uniform throughout the cluster and does not increase appreciably with the cluster size. The average density of the globular clusters is estimated at one star equivalent to the sun per two cubic parsecs, which is about five times the density of the local star system. The absolute maximum, on the basis of the figures previously quoted, is 20 times the local density and the maximum density in the clusters must stay within this limit to keep the system stable. The observed average density indicates that this requirement is met by a substantial margin.

In the light of the points brought out in the foregoing discussion we may conclude that individual stars and clusters of the globular type are continually being formed throughout the vast expanse of inter-galactic space. Each of the individual stars is ultimately captured by one of the clusters or galaxies. The great majority of the clusters also come within the gravitational limit of one or another of the larger aggregates sooner or later and are absorbed, but a few manage to stay out of the way of their voracious larger neighbors long enough to develop into full-sized galaxies. It is not unlikely that the union of two large clusters is the event that marks the advance from cluster to galaxy status, since this not only provides the additional mass needed to speed up the capture of other clusters and smaller units, but also explains the origin of the increased rotational velocity which is characteristic of the galaxies.

Because of the continual pull exerted by the galaxies on all of the clusters within the galactic gravitational limits, we can expect to find each galaxy surrounded by a concentration of globular clusters moving gradually inward. Inasmuch as the original formation of the clusters took place practically uniformly throughout all of this space the concentration of clusters should theoretically continue to increase as the galaxy is approached, until the capture zone is reached. Furthermore, the number of clusters in the immediate vicinity of each galaxy should theoretically be a function of the gravitational force and the size of the region within the gravitational limits, both of which are directly related to the size of the galaxy. All of these theoretical conclusions are confirmed by observation. A few clusters have been found accompanying such small galaxies as the member of the Local Group located in 4 Fornax; there are at least 3 or 4 in the Small Magellanic Cloud and about a dozen in the Large Cloud; our Milky Way System has at least 150 when allowance is made for those which we cannot see for one reason or another; the Andromeda spiral, M 31, has about 200; NGC 4594, the “Sombrero Hat,” is reported to have “several hundred” associated clusters; while the number surrounding M 87 is estimated to be about a thousand. These numbers of clusters are definitely in the same order as the galactic sizes indicated by the criteria previously established. The Fornax-Small Cloud-Large Cloud-Milky Way sequence is not open to question. M 31 and our own galaxy are probably close to the same size but the latest information indicates that M 31 is the larger, as the relative numbers of clusters would suggest. The dominant nucleus in NGC 4594 shows that this galaxy is still older and larger, while all of the characteristics of M 87 suggest that it has reached the upper limit of galactic size.

Here again, as in the case of stellar evolution, observation gives us only what amounts to an instantaneous picture and to support the theoretical deductions we must rely primarily on the fact that the positions of the clusters as observed are strictly in accordance with the requirements of the theory. It is worthy of note, however, that such information as is available about the motions of the clusters of our Galaxy is also entirely consistent with this theory. In the words of Struve, we know “that the orbits of the clusters tend to be almost rectilinear, that they move much as freely falling bodies attracted by the galactic center.” According to the theory that has been developed herein, this is just exactly what they are.

Capture of galaxies by larger galaxies is much less common than capture of globular clusters, simply because the clusters are very much more abundant. We may deduce, however, that there should be a few galaxies on the road to capture by each of the giant spirals, and this is confirmed by the observation that the nearer spirals (the only ones we can check) have “satellites,” which are nothing more than small galaxies that have come within the gravitational field of the larger units and are being pulled in to where they can be conveniently swallowed. The Andromeda spiral, for instance, has at least four satellites: the elliptical galaxies M 32, NGC 147, NGC 185, and NGC 205. The Milky Way galaxy is also accompanied by at least four fellow travelers: the two Magellanic Clouds and the elliptical galaxies in Sculptor and Fornax. The expression “at least” must be included in both cases as it is by no means certain that all of the small elliptical galaxies in the vicinity of these two spirals have been identified.

Some of these galactic satellites not only occupy the kind of positions required by theory, and to that extent support the theoretical conclusions, but also contribute evidence of the second class: indications that the process of capture is already under way. Let us look first at the irregular galaxies. This galactic classification was not given a separate place in the age-size-shape sequence previously established as it appears reasonably certain that these irregular aggregates, which constitute only a small percentage of the total number of observed galaxies, are merely galaxies belonging to the standard classes which have been distorted out of their normal shapes by special factors. The Large Magellanic Cloud, for instance, is big enough to be a spiral and it contains the high proportion of advanced type stars which is typical of the spirals. Why then is it irregular rather than spiral? The most logical conclusion is that the answer lies in the proximity of our own giant system; that the Cloud is in the process of being swallowed by our big spiral and that it has already been greatly modified by the gravitational forces which will eventually terminate its existence as an independent unit. We can deduce that the Large Cloud was actually a spiral at one time and that the “rudimentary” spiral structure which is recognized in this system is in reality a vestigial structure.

The Small Cloud has also been greatly distorted by the same gravitational forces and its present structure has no particular significance. From the size of this Cloud we may assume that it was a late elliptical or early spiral galaxy. The conclusion that it is younger than the Large Cloud reached on the basis of the relative sizes is supported by the fact that the Small Cloud is a mixture of Population I and Population II stars, whereas the stars of the Large Cloud belong almost entirely to the types assigned to Population I in Baade’s original classification.

The long arm of the Large Cloud which extends far out into space on the side opposite our Galaxy is a visible record of the recent history of the Cloud. It should be recognized that the gravitational attraction of the Galaxy is exerted on each component of the Cloud individually, not on the structure as a whole, since the Cloud is not an integral unit but an assembly of discrete units in which the cohesive and disruptive forces are in balance, a balance which is precarious at best in view of the repulsion between the individual units. The differential forces due to the greater distances to the far side of the Cloud were unimportant when the Cloud was far away but as it approached the Galaxy the force differential increased to significant levels. As the main body was speeded up by the increasing gravitational pull it was inevitable that some stragglers would fail to keep up with the faster pace, and once they had fallen behind the force differential became even greater. We would expect, therefore, to find a luminous trail along the recent path of the incoming Cloud: just the kind of a structure that we actually observe.

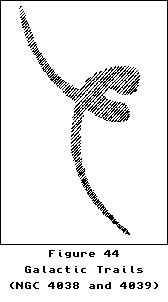
This is no isolated phenomenon. Small galaxies may be pulled into the larger units without leaving visible evidence behind, as the amount of material involved is too small to be detected at great distances, but when two of the large units, the spirals, approach each other we commonly see luminous trails of the same nature as the one that has just been discussed. Figure 44 is a diagram of the structural details which can be seen in photographs of the galaxies NGC 4038 and 4039. Here we see that one galaxy has come up from the lower right of the diagram and has been pulled around in a 90 degree bend. The other has moved down from the direction of the top center and has been pulled to the right and forward. When the action is complete there will be one giant spiral moving forward to its ultimate destiny, leaving the stray stars to be picked up by some other aggregation which will come along at a later time. Several thousand “bridges” which have developed from interaction between galaxies are reported to be visible in photographs taken with the 48 inch Schmidt telescope on Mt. Palomar. Some of these are trailing arms similar to those in Figure 44. Others are advance units which are rushing ahead of the main body. The greater velocity of these advance stars is also due to the gravitational differential between the different parts of the galaxy, but in this case the detached stars are the closest to the approaching galaxy and are therefore subject to the greatest gravitational force.

In order to produce effects of this kind it is, of course, necessary that the smaller unit be well within the effective gravitational limit of the larger. It will therefore be of interest to calculate the gravitational limit of our Galaxy, a typical large spiral, and to compare this distance with the observed separations between some of the objects which are presumably undergoing gravitational distortions. The galactic masses are usually expressed in terms of a unit equal to the solar mass and since we have already evaluated the gravitational limit for this mass we may express equation 157 in the convenient form

d0 = 2.27 (m/m8)½ light years

(158)

The mass of our Galaxy is estimated all the way from 10¹¹ to 5×10¹¹ solar masses. The probable accuracy of these estimates will be discussed later, but if we accept an intermediate value for present purposes equation 158 gives us a gravitational limit of about a million light years. The distance to the Magellanic Clouds is variously estimated from about 150,000 to some 230,000 light years, but in any event it is apparent (1) that the Magellanic Clouds are well inside the gravitational limit of the Galaxy, and (2) that the diameters of the Clouds, approximately 20,000 and 30,000 light years, are large enough in proportion to the distance from the Galaxy to give rise to significant differentials in the effective gravitational forces. The calculation thus verifies the conclusion that the Magellanic Clouds are well on their way to capture by the Galaxy. The diameter of the Galaxy is about 100,000 light years and we may therefore generalize these findings for application to distant systems by observing that considerable deformation and loss of material from a large incoming unit are produced at any distance less than the equivalent of two diameters of the larger galaxy. There are many visual pairs of galaxies which show no indications of gravitational distortion although they appear to be within the two diameter range, but in these instances we must conclude that there is actually a radial separation which puts them beyond the effective distance.

Irregularities of one kind or another are relatively common in the very small galaxies but these are not usually harbingers of coming events like the gravitational distortions of the type experienced by the Magellanic Clouds. Instead they are relics of events that have already happened. Capture of a globular cluster by a small galaxy is a major step in the galactic course of evolution, consolidation with another small galaxy is a revolutionary development. Since the relatively great disturbance of the galactic structure due to either of these events is coupled with a slow return to normal because of the low rotational velocity, the structural irregularities persist for a longer time in the smaller galaxies and the number of small irregular units visible at any particular time is correspondingly large.

Although the general spiral structure of the larger galaxies is regained relatively soon after a major consolidation because of the high rotational velocity which speeds up the mixing process, there are variations in some of these structures which seem to be correlated with recent captures. We note, for instance, that a number of spirals have semi-detached masses or abnormal concentrations of mass within the spiral arms which are difficult to explain as products of the development of the spiral itself, but could easily be the results of captures. The outlying mass, NGC 5195, attached to one of the arms of M 51, for example, has the appearance of a recent acquisition. Similarly the lumpy distribution of matter in M 83 gives this galaxy the aspect of a recent mixture which has not been thoroughly stirred. A study of the structure of the so-called “barred” spirals also leads to the conclusion that these units are galactic unions which have not yet reached the normal form. The variable factor in this case appears to be the length of time required for consolidation of the central masses of the combining galaxies. If the original lines of motion of the two units intersect, the masses are undoubtedly intermixed quite thoroughly at the time of contact, but an actual intersection of this kind is not a requirement for consolidation. All that is necessary is that the directions of motion be such as to bring one galaxy well within the gravitational limit of the other at the closest point of approach. The gravitational force then takes care of the consolidation. Where the gap to be closed by gravitational action is relatively large, however, the rotational forces may establish the characteristic spiral form in the outer regions of the combined galaxies before the consolidation of the central masses is complete and in the interim the galactic structure is that of a normal spiral with a double center.

Figure 45 (a) shows the structure of the barred spiral galaxy NGC 1300. Here the two prominent arms terminate at the mass centers a and b, each of which is connected with the galactic center c by a bridge of dense material which forms the bar. On the basis of the conclusions reached in the preceding paragraph we may regard a and b as the original nuclei of Galaxies A and B, the two units whose consolidation produced NGC 1300. The gravitational forces between a and b are modifying the translational velocities of these masses in such a manner as to cause them to spiral in toward their common center of gravity, the new galactic nucleus, but this process is slowed considerably after the galaxy settles down to a steady rotation as only the excess velocity above the rotational velocity of the structure as a whole is effective in moving the mass centers a and b forward in their spiral paths. In the meantime the gravitational attraction of each mass pulls individual stars out of the other mass center and builds up the new galactic nucleus between the other two. As NGC 1300 continues on its evolutionary course we can expect it to gradually develop into a structure such as that in Figure 45 (b), which shows the arms of M 51. Figure 45 (c) indicates how M 51 would look if the central portions of the arms were removed. The structural similarity to NGC 1300 is obvious.

Another valuable source of information corroborating the theoretical deductions with respect to the capture process is provided by the globular clusters. These clusters are too small to affect the shape of the larger galaxies which may absorb them and they are also too small for the development of noticeable distortion effects within their own structures such as those which we see in the Magellanic Clouds. On the other hand the process of capture of these units is taking place practically on our doorstep and we are able to follow the clusters into the main body of the galaxy and to read their history in much greater detail than is possible in the case of the larger and more distant aggregates.

We see the globular clusters as a roughly spherical halo extending out to a distance of about 100,000 light years from the galactic center. There is no definite limit to this zone; the clusters gradually decrease in concentration until they reach the cluster density of inter-stellar space, and individual clusters have been located out as far as 500,000 light years. Since the visible diameter of the average cluster is in the neighborhood of 100 light years and the actual over-all dimensions are undoubtedly greater, there should be a substantial gravitational differential between the near and far sides of the cluster at distances within 100,000 light years. We can therefore deduce that the clusters are experiencing an increasing loss as they approach the Galaxy, both by acceleration of the closest stars and by retardation of the most distant. The effect of slow losses of this kind on the shape of a nearly spherical rotating aggregate is minor and the detached stars merge with the general field of stars which is present in the same zone as the clusters. The process of attrition is therefore unobservable from our location, but we can verify its existence by comparing the sizes of the clusters before and after losses of this kind have taken place. Studies which have been made on the clusters accessible to observation indicate that the average size of the units at 25,000 parsecs from the galactic center is 30 percent greater than the average size of those only 10,000 parsecs distant. From this it would appear that the cluster loses more than half of its mass by the time it reaches what may be regarded as the capture zone, the region in which the gravitational action is relatively rapid.

In this capture zone the losses are still greater and by the time the cluster arrives in the vicinity of the galactic plane the remaining stars are numbered in the thousands instead of in the tens or hundreds of thousands. On entry into the rapidly rotating spiral disk still further disintegration occurs, and the original globular cluster becomes a number of separate galactic clusters, the largest of which has only a few hundred members. Since the gravitational attraction of this small group is not sufficient to offset the effect of the non-uniform rotational forces of the Galaxy, the galactic clusters slowly break up and the individual stars go their separate ways. In the meantime, however, the evolutionary development of the stars is speeded up by the greatly increased amount of “food” available in the galactic disk and the stars in the older galactic clusters are quite different from those in the units just making the transition from the globular to the galactic status.

This evolution of the constituent stars is the feature which enables us to identify the relative ages of the clusters and thereby to confirm the theoretical deductions as to the history of these units. The original globular clusters are relatively young aggregates and the spread between the oldest and youngest stars in each cluster, excluding strays from older systems that may have been picked up along the path, only represents a fraction of the total evolutionary cycle. After the cluster arrives in the immediate vicinity of the Galaxy it ceases to grow and there is no further increase in the age spread. The sector of the cycle on the H-R diagram occupied by the constituent stars then simply moves forward around the circle as the cluster grows older and passes through the various evolutionary stages.

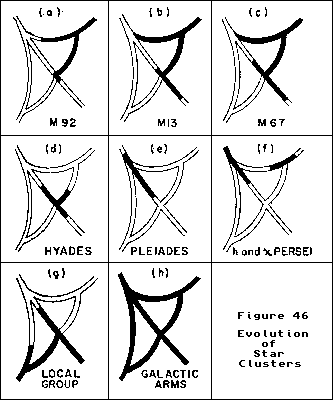
Figure 46 is a series of clusters arranged in order of increasing age. As a means of facilitating identification of the position of each group with reference to the complete evolutionary cycle, the entire stellar cycle is shown in outline in each diagram and the sectors occupied by the stars of the particular group are filled in with heavy lines. We have already noted that the globular clusters are composed of very young stars in the early evolutionary region at the upper right of the H-R diagram. In Figure 46, diagram (a) shows the composition of a typical globular cluster, M 92. Here the most advanced stars have barely reached the main sequence, the youngest are still in the formation zone, and the great majority of the constituent stars are in the intermediate region on one of the paths AB or AD. Diagram (b) is a similar representation of the globular cluster M 13, which is in a slightly more advanced stage, a larger proportion of the stars having arrived in the lower section of the main sequence. The composition of the galactic cluster M 67, diagram (c), is very similar to that of M 13, indicating that M 67 is a very recent arrival in the galactic disk, a conclusion which is corroborated by the fact that this is one of the most populous of the known galactic clusters and one of the highest above the galactic plane (about 440 parsecs). In an older cluster, the Hyades (d), a few stars still remain on the contraction path AB but the majority have reached the main sequence. Next is a still older cluster, the Pleiades   (e), in which the last stragglers have attained gravitational equilibrium and the entire body of stars has moved up along the main sequence.

Further development of the Pleiades cluster in the future will bring the hottest stars in this group to the destructive limit at the top of the main sequence and will cause these stars to revert back to the red giant status via the explosion route. In the double cluster h and X Persei (f) we find that such a process has already begun. Here the main body of stars is in the region just below the upper limit but a number of red giants are also present. We can identify these giants as explosion products rather than new stars as the former explanation keeps all of the stars in the cluster in an unbroken sequence along the evolutionary path, whereas if these were young stars of cycle A they would be totally unrelated to the remainder of the cluster: a highly improbable situation.

The identification of still older clusters of stars is more difficult because the stars of the clusters separate in the course of time and there are some problems involved in recognizing these stellar associations when they are no longer compact groups. It appears probable, however, that the sun and its immediate neighbors constitute a group with a common origin and diagram (g) represents the stars of this Local Group. Here we have evidence that the group is well along in the second cycle. There are no giants among these stars but the presence of white dwarfs in such systems as Sirius and Procyon and the planets in the solar system shows that the group has been through the explosion phase. We may interpret the lack of red giants as indicating that the former giants such as Sirius have had time to get back to the main sequence while their slower white dwarf companions are still on the way. It is not certain that all of the nearby stars actually belong in this same age group, as some younger stars may also be present, but there are no obvious incongruities. Finally in diagram (h) we have the full complement of Population I stars as found in the spiral arms, an assortment which includes stars in all phases of the evolutionary cycle.

Thus far the terms Population I and Population II have been used in the customary manner to refer to the two general classes of stars first distinguished by Baade, and characterization of the stars of Figure 46 (h) as Population I follows this practice. As the diagram shows, however, classifying the stars of the spiral arms as Population I makes this category so broad that its usefulness is severely limited and it therefore seems appropriate to modify these classifications to bring them into line with the relations which have been developed in the foregoing pages. The general significance of the two designations will be retained but new definitions will be set up, based on position in the evolutionary cycle. In this revision the Population I designation will be applied to main sequence stars only, and all of the pre-main sequence stars will be assigned to Population II. These I and II classifications will then be subdivided according to the particular evolutionary cycle in which the stars are located, using the letter A to refer to the first cycle (the pre-explosion stage) and B, C, etc., to identify the subsequent cycles.

On this basis the early type first cycle stars of the globular clusters and elliptical galaxies, which were placed in Population II by Baade, will fall in Population II-A. The stars of the galactic clusters (except the very young systems such as M 67) and the other first generation main sequence stars of the spiral arms, which formed part of Baade’s Population I, will become Population I-A. In most spiral galaxies the stars of the nuclei resemble those of the globular clusters and were included in Population II in the original classification. From the facts that have been developed herein it is apparent that these are actually the oldest stars in the galaxies and they do not belong with the young stars of the clusters. They are similar to the latter in many respects only because they have gone all the way around the cycle and are back to the same position on the H-R diagram that is occupied by the young stars. Under the new definitions this position keeps the stars in Population II but since they are in the second cycle the classification is II-B. The second generation main sequence stars, the group to which the sun belongs, are Population I-B.

Theoretically the stars of the galactic nucleus should continue moving around the cycle as they grow older, until the galaxy finally reaches the end of its life span, but detailed observation of the individual stars in this region is feasible only to a very limited degree with the facilities now available and it is difficult to determine just how far this cyclic course actually extends. We do observe, however, that the light from the nucleus of a galaxy does not always have the red color characteristic of the Class II populations. In a number of galaxies, perhaps as many as ten percent of the total, the light from the galactic center is reported to be as blue as that from the disk. This indicates that in these units a large proportion of the total light is coming from the most advanced members of Population I-B. The existence of I-B stars in relatively large numbers in other nuclei may then be inferred, since the presence of the upper main sequence stars of the second generation in some nuclei means that many slightly younger galaxies must contain lower main sequence stars of the same cycle. These early I-B stars are in the same spectral classes as the II-B group and cannot be distinguished by color. The same is true of the II-C stars, the class which follows the late type I-B stars that are responsible for the blue color in galactic nuclei where it appears. We can logically infer than at least some of these II-C stars are present but we cannot identify them in the nuclei with the facilities now available, and we cannot determine whether still older populations are present.

From the foregoing it can be seen that the characteristics of the composite light emitted by a galaxy or by one of its constituent parts constitute another means of identifying the age of the aggregate, supplementing the criteria previously discussed. The integrated light from the elliptical galaxies belongs to spectral type G. In the early spirals the emission rises to type F, or even A in some cases, because of the large number of stars which move up to the higher portions of the main sequence. As these stars pass through the explosion stage and revert to the II-B status, accumulating largely in the galactic nucleus, the light gradually shifts back toward the red and in the oldest spirals the color is very much like that of the elliptical galaxies. Summarizing this color cycle, we may say that the early structures are red, there is little change in the character of the light during the development of the elliptical galaxy, then a rapid shift toward the blue as the transition from elliptical to spiral takes place, and finally a slow return to red as the spiral ages. In order to lay the foundation for an explanation of these variations in the rapidity of change it will now be necessary to take up a consideration of the behavior of the interstellar dust and gas.

Since matter is continually forming throughout all space and is moving hither and yon under the influence of gravitation and other forces, there is a certain minimum amount of material subject to accretion in any environment in which a star may be located. Immediately after the formation of a star cluster by condensation of the denser aggregates of matter in a particular volume this thin diet of primitive material is all that is available for growth and the development of the structure is correspondingly slow. As time goes on the rate of action speeds up when material begins to arrive from the more distant regions which were not stripped of their substance by the initial condensation process. Furthermore, the increasing mass accelerates the rate of progress considerably as it not only extends the gravitational limit and puts additional material within reach but also makes the capture of larger aggregates feasible. As we have already noted, observation shows that the larger elliptical galaxies have reached the point where they are beginning to pull in globular clusters in addition to single stars and diffuse material.

We cannot see what is happening to the non-luminous material, but this matter is subject to the same gravitational forces as the luminous aggregates, and we can deduce that when the elliptical galaxies reach the size that permits them to start capturing globular clusters they simultaneously begin picking up pre-stellar clouds of similar size. The dust and gas clouds arrive too late in the elliptical stage of galactic evolution to have much effect on the properties of the elliptical units, although they are no doubt responsible for the development of the small representation of hot blue stars previously mentioned. But when the elliptical structure breaks up and spreads out to form the spiral, the stars of the galaxy are thoroughly mixed with the recent acquisitions of dust and gas and the stage is set for a period of rapid advance along the path of stellar evolution. This relatively fast progress is still further magnified when it is viewed from the standpoint of light emission since the hot stars at the upper end of the main sequence may be thousands of times as luminous as the average Population II star.

The identification of these conspicuous hot and luminous stars with the spiral arms was the step which led to the original concept of two distinct stellar populations, but the new information which has been developed herein makes it clear that the galactic arms actually contain a rather heterogeneous population and a more definite correlation between the various types of stars and the general stellar populations is in order. Population I as herein defined is composed entirely of stars of the main sequence, the most conspicuous being the blue giants at the top of the sequence. The various classes of hot and massive shell stars also belong in this group and we can include the supernovae, which mark the end of the dense phase of the stellar cycle. The Population II stars of all cycles on the minimum accretion branch are the red giants and sub-giants. The white dwarfs join this group after the first explosion; that is, in Class II-B and beyond.

The rapid accretion branch of the Population II-A stars is a group of variable stars sometimes called Type II Cepheids and including, in the order of increasing age and decreasing period, the stars of the RV Tauri, W Virginis, and RR Lyrae groups. The II-B variables, the corresponding stars of the next cycle, are similar but not identical and the groups which make up this class, listed in the same order as before, are the long period variables, the semi-regular variables, and the classical Cepheids. Since these are second generation stars they are binary or multiple systems and they are shifted upward on the H-R diagram relative to the corresponding II-A stars. According to recent determinations, the average difference in luminosity for stars of the same period is about 1½ magnitudes. Population II-B also includes a similar group of variables on the other side of the main sequence which is absent from the pre-explosion Population II-A. Here we have, also in the order of increasing age, the planetaries, the classical novae, the recurrent novae, and the dwarf novae of the U Geminorum and similar types. Population II-C and later variables no doubt extend the differences between the II-B and II-A classes still farther, but this point cannot be checked against observation because the available information regarding the third cycle stars is still quite incomplete. Table CXII is a summary of the stellar types included in each classification.

Table CXII
Composition of Stellar Populations

Population I (all cycles)
	Main sequence stars
	Shell stars
	Supernovae
Population II
Stable stars (all cycles)	Red giants
	Sub-giants
Stable stars (II-B and later)	White dwarfs
Variable stars (II-A)	RV Tauri
	W Virginis
	RR Lyrae
Variable stars (II-B)	Long period variables
	Semi-regular variables
	Classical Cepheids
	Planetaries
	Classical novae
	Recurrent novae
	Dwarf novae

From the nature of the growth processes as they have been described it is apparent that no aggregate consists entirely of a single stellar population, but the very young structures approach this condition quite closely since these young aggregates are formed from young stars and the only dilution by older material results from picking up an occasional stray such as one of the stars that are left behind on trails similar to those shown in Figure 44. The earlier globular clusters, under normal conditions, are therefore practically pure Population II-A and their H-R diagrams are similar to that of M 92, Figure 46 (a). The component stars are red giants, sub-giants, and variables of the RR Lyrae and other II-A groups. In the older globular clusters and the elliptical galaxies some of these same stars are present but a substantial number of stars have reached positions on the main sequence. On the basis of the classification which has been set up in this work both the older globular clusters and the elliptical galaxies will have to be regarded as being composed of mixed II-A and I-A populations. The earlier galactic clusters are in the same evolutionary stage as the elliptical galaxies and the H-R diagrams of M 67 and the Hyades, Figs. 46 (c) and (d), are to some extent representative of the phases through which the elliptical galaxies pass, although it should be remembered that the early end of the age distribution is not cut off in the growing galaxies as it is in the disintegrating clusters and the diagram for an elliptical galaxy in the same evolutionary stage as the Hyades would extend the sector occupied by the Hyades stars all the way back through the globular cluster sector to the original zone of star formation.

The rapid development in the early spiral stage eliminates most of the II-A units, except those in the incoming stream of captured material, and the stars of these early spirals are predominantly Population I-A. Further aging of these spirals then results in the appearance of second generation stars, beginning with Population II-B. The fact that the development of the spiral structure antedates the formation of the second generation stars results in a general distribution principle which has important implications for observational astronomy. With the qualification “except for strays from older systems” which will have to be understood as attached to all statements in this discussion of stellar populations, we may say that the second and later population stars, long period variables, classical Cepheids, white dwarfs, novae, etc., are confined exclusively to the stellar disks (including the nucleus). At the other extreme the early first generation stars (Population II-A) are distributed throughout all space, with the main sequence stars of the first generation (Population I-A) occupying an intermediate position.

In our own galactic system, for example, we find the typical Population II-A stars, red giants and RR Lyrae stars, in all of the observable region surrounding the Galaxy, both as individuals and in the globular clusters. On the other band, the classical Cepheids and the novae, the most easily identified of the second generation stars, are strongly concentrated toward the galactic plane and these stars are not found in the globular clusters. A few long period variables have been reported in the globular clusters and among the high velocity stars which are outside the disk of the Galaxy, but the large degree of irregularity in these stars makes it rather difficult to classify them accurately and it seems likely that these apparently misplaced second generation stars are actually long period Type II variables (Population II-A). The distribution of the white dwarfs cannot be determined from observation as they are too faint to be seen at great distances, but we can at least say that there is no evidence which conflicts with the theoretical conclusions as to the evolution of these stars.

One of the very significant points brought out by the theoretical development is that the first cycle stars should be single units whereas those of the second and later cycles should be binary or multiple systems. The second part of this conclusion is given strong support by statistical studies of the stars in the local environment. These studies indicate that about two-thirds of the near-by stars with masses greater than that of the sun are binaries or multiple stars. As the stellar mass decreases this proportion falls off rapidly but the reason for this is clearly indicated in the previous discussion of the formation of planetary systems. We know that a planetary system can be formed in lieu of a binary star when the central mass is equal to that of the sun, and it is obvious that a smaller stellar mass is still more favorable for the appearance of a planet or system of planets rather than a star as the minor component of the post-explosion star system. The drop in the proportion of binary stars as the mass decreases is merely a reflection of the shift from visible stars to invisible stars or planets; it does not indicate any actual decrease in the number of two-component systems. The absence of binary or multiple units in the first cycle stars is more difficult to establish because of the relative inaccessibility of these stars, and the evidence thus far available is somewhat spotty. There are a number of reports of binary stars in the galactic clusters, where they should theoretically be absent except in Cycle B clusters and in the post-explosion members of the most advanced Cycle A units, such as the double cluster in Perseus. If any binary stars are actually present in the early type galactic clusters they are probably stars which have become mixed with the cluster stars during the entry of the cluster into the galactic disk.

It should be recognized, however, that the identification of some of these clusters as Cycle A structures is only tentative. It appears that the break-up of the clusters should proceed more rapidly than the evolution of the stars of which they are composed and for this reason the easily distinguished, homogeneous clusters are presumed to be relatively recent additions to the Galaxy. It is not impossible, however, that some of these clusters may have evolved quite rapidly and are already in the second cycle. We have already noted that the stellar evolution speeds up considerably in regions of high dust and gas concentration. A good illustration of the way in which the normal relationship between chronological age and evolutionary age can be modified by such an environment is provided by the globular clusters which are located in the Large Magellanic Cloud. Here the gravitational distortion of the galactic structure has resulted in an irregular distribution of the dust and gas clouds and some globular clusters have entered high density regions of this kind. As a result the evolution of the stars in these clusters has been much faster than normal and while the shape, size, and location of these clusters are those of normal globular clusters, the stars are similar to those of the galactic clusters: members of Population I-A. If the high percentages of binary stars reported by some observers for such clusters as Praesepe and the Hyades are confirmed it will be necessary to revise the tentative conclusions as to the evolutionary stage of these clusters and place them in Cycle B. There are also a large number of loose, heterogeneous clusters which quite definitely belong in the second cycle. One group of this kind which has been given extensive study is NGC 6231. Here we find a large proportion of Population II stars, indicating that this cluster is either considerably older or considerably younger than a main sequence cluster such as the Pleiades. Since the structure, or lack of structure, of the cluster indicates that it has undergone severe modification since entering the Galaxy we conclude that it is older and that the Population II stars belong to Class II-B. This conclusion is supported by evidence which indicates that the stars of the cluster are largely binaries.

As mentioned in the discussion of the spiral structure, the material of which a galaxy is composed is in such a physical condition that it has the general characteristics of a fluid. In such an aggregate the heavier material moves toward the center of gravity, displacing the lighter units, which concentrate in the outer regions (the galactic disk). The dust and gas clouds and the early type stars are therefore found mainly in the disk while the older and heavier stellar systems sink into the nucleus. The segregation process is very slow and irregular because of the effects of the galactic rotation and in spite of the general separation of the older material from the younger it can be expected that many of the older star systems will be found scattered through the predominantly Cycle B population of the spiral disk. The average mass of these systems is greater than the corresponding average of any of the earlier groups but in view of the large variation between individuals within any group this characteristic is not a positive means of identification. Multiple systems are more distinctive. From the points brought out in the discussion of the formation of planetary systems it can be seen that the ultimate result of a stellar explosion is a binary star or star and planet, probably with some additional small companions. While it is possible that one of these companions may be large enough to qualify as a star, the nature of the aggregation process is such as to make this quite unlikely, and in general we may regard a multiple star system as one which has passed through the explosion stage more than once.

It has been estimated that five percent of all visual binaries are members of multiple systems. In addition to these systems in which evidence of multiplicity has been detected by observation, there are also a substantial number of observed binaries which are associations of two type A stars or two type B stars and which, according to the binary star theories that have been developed, must have additional unseen components on the other side of the main sequence. The systems of the Algol type, for instance, consist of main sequence stars paired with sub-giants of somewhat smaller mass. The main sequence star cannot be the B component because it is the larger of the two units and the more advanced from an evolutionary standpoint, and the sub-giant cannot be the B component because it is above the main sequence. We must therefore deduce that these star systems have undergone a second set of explosions and that each of the observed stars is accompanied by a small B component. As mentioned earlier, at least one and possibly both of the additional components predicted by theory have been located in Algol itself and the theory merely requires that the other systems of the same kind be similarly constructed.

We have seen that the two stars of a binary system tend to approach equality of mass as they near the upper end of the main sequence. When one explodes the other should follow suit within a relatively short time, particularly since it will receive substantial amounts of matter and thermal energy from its disintegrating companion. The great majority of multiple systems should therefore contain even numbers of stars. The normal progression is from binaries to four-member systems such as Algol and then to six-member systems on the order of Castor. The latter may be regarded as one of the oldest star systems within our field of vision.

We have found thus far in our examination of the aggregation process that the primary units of matter, the atoms, respond to the gravitational forces by continually combining until they finally build up into units of the maximum size possible for simple aggregates. These secondary units, the stars, likewise gravitate into still larger aggregates, the galaxies. The question now arises, is this the end of the aggregation process or do the galaxies again combine into super-galactic aggregates? The existence of many definite groups of galaxies with anywhere from 10 to 1000 members would seem to provide an immediate answer to this question, but the true status of these groups or clusters of galaxies is not clear as that of the stars and the galaxies. Each of the stars is a definite and tangible unit, constructed according to a specific pattern from subsidiary units which are systematically related to each other. The same can be said of the galaxies. It is by no means certain, however, that this statement can be applied to the clusters of galaxies; on the contrary, the information now available suggests that it cannot.

Let us then turn to a theoretical examination of the question. It is immediately apparent that the basic situation is very similar to that involved in the combination of stars into galaxies. All of the smaller units which are formed within the gravitational limit of a giant spiral, or are brought within it by the relatively rapid extension of the limit due to the growth of the galaxy, are ultimately consolidated with the spiral; those outside this limit are continually receding. The question then reduces to a matter of whether or not the galaxies can extend their gravitational influence still farther by the formation of super-galaxies in the same manner that the stars extend their gravitational limits by the formation of star clusters. The mathematical relations are similar and since we find that the minimum star cluster contains thousands of stars we must conclude that if there are any super-galaxies the small clusters of galaxies now recognized do not meet the requirements. On the other hand we know from observation that our Galaxy cannot be a member of a giant super-galaxy since all galaxies other than the few in our immediate vicinity are observed to be receding. (According to theory the members of the Local Group, are also moving outward away from us but this movement is so slow that it is masked by the random motions of the galaxies.) Furthermore, the recession is observed to be uniform throughout the vast space accessible to present-day telescopes and it therefore follows that super-galaxies cannot exist anywhere in this region of space.

Another line of reasoning brings us to the conclusion that the situation which we find in the observable region is typical and that there are no super-galaxies. The Fundamental Postulates require all basic processes to be cyclical, and the formation of super-galaxies is therefore impossible unless a process also exists whereby their existence can be terminated. But there are no more destructive limits on which such a process could be based. The lower and upper destructive limits of matter are reached in the supernovae and the mature galaxies respectively, and there are no others. We must therefore conclude that the existence of super-galaxies is inconsistent with the postulates.

What, then, is the nature of the observed clusters? A clue to the answer to this question can be found by examination of the contents of these groups. In our Local Group, for example, we find three major spirals, in which the bulk of the mass is concentrated, and fifteen or twenty small units. A striking contrast is supplied by the Coma cluster which contains at least 800 units, but few, if any, spirals. When we take a second look at this situation, however, it becomes apparent that the difference between the two groups is merely a matter of age. The Coma cluster is a relatively young aggregation in which the individual units are numerous but small; the Local Group is an old system in which the greater part of the mass has gravitated into a few large galaxies. Each of these giants is equivalent to 100 or more of the elliptical galaxies of the Coma cluster and when we take this factor into consideration the two groups are seen to be associations of comparable size, differing only in age and the characteristics accompanying age. We have already deduced that new galaxies are formed in regions which have been left vacant by the outward motion of the previously existing galaxies. Presumably this process can and does take place on a single galaxy basis in many, if not most, instances but the galactic associations can easily be explained if we recognize that larger regions will on occasion be left open through chance, and still further irregularities in the size of these vacant regions will be introduced through the disappearance of the mature galaxies by means of a process which will be discussed later. When an extensive region is thus left vacant new galaxies begin to develop throughout all of this empty space and because these galaxies originate at approximately the same time they pass through the various stages of evolution together and we can recognize the same kind of age characteristics in each group as a whole that we normally see in the individual galaxies.

The very early groups, those whose largest aggregates are globular clusters or the loose irregular galaxies resulting from the union of two or three clusters, are invisible unless relatively close. As the growth process continues the regular elliptical form is developed and the groups arrive at the stage represented by the Coma cluster and the cluster in Corona Borealis, in which there are a large number of small elliptical and irregular galaxies spaced relatively close together. Here the characteristics of the group as a whole are identical with the characteristics of the individual elliptical galaxy. Almost all of the component stars belong to the first generation families, Populations II-A and I-A, the composite light from the cluster is red, and there is no evidence of dust accumulations. As the group ages it decreases in numbers because of the consolidation of units but it spreads out into more space. While these processes are taking place the other signs of maturity appear: spiral galaxies are formed and go through their evolutionary stages, stars of the hot massive types are developed, and so on. In the later stages the cluster is essentially nothing more than a region of approximately average concentration in the general field of galaxies.

A highly significant fact about these mature groups of galaxies is that the giant spirals into which most of the mass has been concentrated are in general well outside the gravitational limits of their nearest contemporaries. In the-Local Group, for example, the gravitational limit of M 31 is in the neighborhood of one million light years, whereas the distance from the Milky Way is double this figure. The average distance between bright galaxies of all kinds has been estimated at 2.4 million light years. Even within the groups, therefore, the major units have a general outward motion, although this velocity is small and the direction of the net movement can be reversed in any individual case by the random motion of the galaxy.

Calculation of the velocities of recession is complicated by uncertainties as to the true masses of the galaxies and the inter-galactic distances, but we may utilize the best available information to arrive at some tentative figures for comparison with the values indicated by the spectral red shifts. As we have found previously, equilibrium between the gravitational force due to the atomic rotation and the force of the space-time progression is reached when the gravitational force has unit value in each effective time region dimension. At greater distances the gravitational force falls below the level of the space-time force, which means that from this point on the net resultant of the two forces is directed outward rather than inward. Gravitation does not actually reach zero as long as it amounts to the equivalent of unity in at least one time region dimension but it vanishes on dropping below this unit level, as less than unit force, does not exist. We may express the equilibrium at the limiting distance, d₁, by substituting unity for the expression 9 × (156.44)³ in equation 156, which gives us

m / (156.44 d12) = 1

(159)

The limiting distance beyond which all galaxies recede with the full velocity of light then becomes

d1 = m½ / 12.5

(160)

which can be expressed in terms of solar masses as

d1 = 13350 (m/m8)½ light years

(161)

The mass of the Galaxy is a difficult quantity to measure and the most recent determinations run all the way from 10¹¹ to 5.0×10¹¹ solar masses. If we accept the highest value for our tentative calculations, d₁ becomes 13350 (5×10¹¹)^½ = 9440×10⁶ light years. Between d₀ and d₁ the decrease in gravitational velocity and the corresponding increase in the velocity of recession are linear. Disregarding the relatively short distance between the Galaxy and d₀, we may then calculate the distance from our Galaxy to any other galaxy of the same or smaller mass by converting the red shift in the spectrum of that galaxy to natural units and multiplying by 9440×10⁶ light years or 2900×10¹¹ parsecs. In Table CXIII the distances thus obtained are compared with a few of the values calculated from observational data.

Table CXIII
Relation of Red Shift to Distance

Cluster	Velocity km/sec	V/V1	Distance (millions of parsecs)
			Calculated	Observed
Virgo	1200	0.004	12	10
Ursa Major	15000	0.050	145	100
Corona Borealis	21500	0.072	210	150
Bootes	39000	0.130	375	250
Hydra	61000	0.203	590	400

In view of all the uncertainties that enter into these calculations, the uncertainty as to the true mass of the Galaxy, the confused state of the distance determinations since the overthrow of the previously accepted yardsticks, and the possibility that some factors may have been overlooked in the very considerable extension of theory upon which the calculations are based, the best that can be expected is to arrive at comparative values which are of the same general order of magnitude and the amount of divergence between the figures in the last two columns of Table CXIII is not significant. The calculations lead to a value of 104 km/sec per million parsecs for Hubble’s constant, the relation between red shift and distance. The 1954 distances shown in Table CXIII correspond to a constant of about 150, some more recently published values fall between 80 and 90, and it has been suggested that the true figure may be as low as 55. Since the accepted value before 1952 was 540 km/sec per million parsecs it is apparent that this whole situation is rather fluid at present and no firm conclusions are warranted. The calculated value would be increased to 230 km/sec per million parsecs if the minimum estimate of 10¹¹ solar masses were used as the mass of the Galaxy, and it could just as easily be reduced below the 104 figure by an upward revision of the Galactic mass.