Chapter 3
BASIC RELATIONS
Because of the reciprocal relationship between space and time and the limitation of both of these quantities to discrete units there are important differences in the various physical phenomena depending on whether the magnitudes involved are above or below the unit levels. We may conveniently regard these unit levels as dividing the universe into several general regions. At one extreme where space is less than unity there are time units only and space, as such, does not exist. This we will call the time region. Next we have a region in which one or more units of space is associated with a greater number of units of time. this region where the space-time ratio, or velocity, is below unity will be termed the time-space region. A similar region on the other side of the neutral axis where the space-time ratio is greater than unity is the space-time region, and at the far extreme we have the space region, where time is less than unity and therefore has no actual existence.
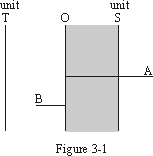
If we set up a scale representing space we may depict magnitudes in the first two of these regions as in Figure 3-1. The line OA is a magnitude in the time-space region extending from zero space to n units of space. The space displacement is represented by the portion SA of the line and is equal to OA minus one unit. From a purely numerical standpoint it should be possible to indicate a magnitude in the time region by a similar shorter line since the space equivalent of a time region quantity is a fraction of a unit, but it will be noted that this would put the entire quantity within the area of zero displacement, whereas time region quantities actually do have time displacements. It is therefore necessary to represent the time region quantity OB as extending in the opposite direction from infinite time (the equivalent of zero space) to B units of time (equivalent of 1/B units of space).
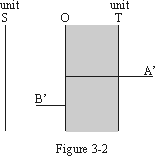
We cannot show magnitudes in the space-time and space regions on this same diagram as the initial point at zero time is equivalent to infinite space and cannot be adequately represented on a finite scale. However, if we change to a time scale we can draw the lines OA’ representing a space-time region quantity and OB’ representing a space region quantity (Figure 3-2) in the same positions as OA and OB in Figure 3-1.
It should be noted that no magnitudes can extend to the left of unit space in Figure 3-2 since this would represent less than unit space, which by the First Postulate is time and hence will be shown in in the direction OT. Similarly in Figure 3-1 no quantities can extend to the left of unit time. If we start at zero space (infinite time) and proceed in the direction of increasing space we will first decrease time displacement. The boundary line of the time region is reached when the time displacement becomes one unit (OB = OT in Figure 3-1). Any further increase in space requires a reversal of direction and entry into the time-space region along the line OA. It is important to note that the quantity transferred to the time-space region in this transaction is one displacement unit and the resultant time-space magnitude is not the one unit quantity OS which corresponds to zero displacement but OS plus the one unit initial level.
Any one-dimensional magnitude makes the transition from the time region to the time-space region immediately on reaching unit displacement. Two-dimensional and three-dimensional magnitudes, however, cannot enter as a whole into the time-space region until unit displacement has been reached in all dimensions. these multi-dimensional quantities may therefore exist in intermediate conditions in which one or two dimensions may have entered the time-space region while the remainder are still in the time region. Since this partial transition will have an important effect on physical properties we will recognize an intermediate time region between the time and time-space regions and a similar intermediate space region on the space side of the neutral axis.
To begin an examination of the regional characteristics we will look first at the time-space region, where units of space are associated with units of time. In the absence of space-time displacement any location A in space moves n space units in n units of time, since the ratio of space to time under these conditions is unity. Location A at time A therefore becomes A+n at time A+n. It should be emphasized particularly that this statement does not refer to some object that might occupy the location A, it refers to the location itself. Of course, if no other factor intervenes any object which might occupy location A at time A would also be found at location A+n in space after n units of time had elapsed, but this would not involve any movement of the object itself. The object remains at rest in space-time but the location in space which it occupies moves.
This concept of space location as a constant progression rather than an entity at rest may seem somewhat confusing at first glance but it is merely an extension of the universally accepted concept of the progression of time. As pointed out earlier, the assumption of progressive time with stationary space could be reversed so that we would have progressive space and stationary time: a hypothesis which in most simple relations would serve equally as well as the more conventional assumption. Since we have postulated time and space as reciprocal forms of the same entity, however, it becomes apparent that the progression is a joint phenomenon resulting from the mathematical equality of the two space-time components in the undisplaced state.
Generalizing the relations brought out in the foregoing discussion we may say that any two undisplaced locations within the time-space region, which differ by n units of space also differ by n units of time. When an additional m units of time have elapsed they differ by n+m units of time and also by n+m units of space, since the ratio of space to time, the velocity of the space-time progression, is unity in this region as a consequence of the equivalence of the undisplaced space and time units.
According to the Second Fundamental Postulate space and time are absolute in magnitude. Velocity, the ratio of the two, is therefore also absolute, but this does not mean that velocities are directly additive. If the velocities are low the departure from an additive relation is so small that no appreciable error is introduced by neglecting it. For instance, if two trains start from the same point and travel in opposite directions at velocities of 50 miles per hour each, we can say that the relative velocity, the rate at which the two trains move away from each other, is the sum of the two, or 100 miles per hour.
But if we replace these relatively slow-moving rains with two objects moving at unit velocity the situation is quite different. Object A moves unit distance in one direction in unit time. Object B moves unit distance in the opposite direction in unit time. the two objects are now separated by two units of distance and if we were to adopt the “uniform flow” theory of time we would say that since the separation amounting to two units of space was accomplished in one unit of time the velocity was two units of space per unit of time, which maintains the additive relation. But the principles brought out in the previous discussion show that the separation in time between objects A and B is not one unit but two units and the relative velocity is 2/2 or unity. The same relation will hold good regardless of the angle between the directions of motion.
This brings us back to the fact that unit velocity is the condition of rest in the space-time universe, the zero level of activity. Unit velocities add up to unit velocities in all directions simply because the sum of any number of zero components is zero. The real magnitude of any other velocity is not the numerical measurement of the velocity itself but the velocity displacement: the departure from unity. Small velocities can be added without introducing any appreciable error because the corresponding displacements are large and the error due to ignoring the one unit of difference between velocity and displacement is negligible, but this error increases as the velocities become greater. In the limiting case where unit velocity is added to or subtracted from another velocity the velocity displacement is not changed at all.
The converse of this proposition is that where unit velocity is measured in some manner, the measurement is always the same regardless of the system of reference. It is immaterial, for instance, whether the measured quantity is the sum of the reference velocity and unit velocity or the difference between the two since the result is the same in either case: a+0 = a-0. This is a principle of some importance and we may express it specifically as follows:
Unit velocity has the same magnitude relative to all reference systems.
The validity of the foregoing statement has been substantiated by careful measurement, notably in the celebrated Michelson-Morley experiment, and the inability of Newtonian mechanics to supply an adequate explanation for it provided the incentive for the development of Einstein’s relativity theory. We can concur in Einstein’s second postulate, the constancy of the velocity of light, which we find to be merely one aspect of the status of unit velocity as the condition of rest in the universe, but we cannot go along with the relativity theory any farther as neither the first Einstein postulate, which denies the existence of absolute velocity, nor the concept of space-time as four-dimensional, is in accord with the findings of this work.
It is interesting to note in this connection that those consequences of the relativity theory which have been the most difficult to reconcile with ordinary human experience are reduced to readily acceptable terms by the postulate of three-dimensional time. For instance, proponents of the relativity theory have indulged in the interesting speculation that if it were possible for someone to leave the earth and travel on a rapidly moving object through space, returning at some later time, the elapsed time on the rapidly moving object would be less than the elapsed time on earth and consequently the individual would return to find that all of his associates had grown old during the (to him) brief interval that he was gone. Such sensational but highly incredible possibilities are flatly denied by the concept of absolute three-dimensional space-time. From the relations which have been developed in this work we find that the hypothetical traveler would indeed move away from the earth in time as well as in space but on his return trip he would reverse his direction both in time and in space and at the end of his journey would be back to earth time. Furthermore, his clocks, contrary to the relativity assumptions, would not alter their registration, his aging would continue at the normal rate, and the time difference through which his frame of reference passed would remain unknown to him. Clocks merely indicate the relative motions of their parts, relations which are totally unaffected by the velocity of the system in which they are situated.
Where no impediment to motion exists only unit velocity is possible. Hence if there is any displacement of space-time whereby the amount of one component becomes greater than than of the other there must be a reversal of direction so that the same unit of the smaller component can be traversed repeatedly. This is a vibratory motion, which we call a frequency.
A frequency greater than unity is a multiplace space vibration; that is, n units of space per unit of time. This is quite easily visualized. We could, for example, construct an instrument in which a pointer moves back and forth over a fixed path. If we adjust the speed of movement so that the pointer traverses the full path in exactly one unit of time we have a representation of unit frequency. then if we speed up the movement we can cause the pointer to traverse its path n times in one unit of time. Here we have a frequency of n units of space or half-cycles per unit of time. A frequency less than unit is a multiple time vibration: n units of time per unit of space. Although this is somewhat more difficult to visualize it is clearly the same thing in the reciprocal form.
This vibratory motion provides us with an illustration, which shows how it is possible for n units of time (or space) to be associated with one unit of space (or time) in a particular phenomenon, even though basically a unit of space and a unit of time are equivalent. In undisplaced space-time there is a progression of one unit of space from A to B simultaneously with the progression of one unit of time from A to B. Because of the directional properties of the universe, however, we may have a second unit of time progressing in the original direction AB to C, while space reverses and progresses one unit from B to A. The motion as a whole then involves two time units AB and BC, but only one space unit AB, which has been traversed in both directions.
Looking at this situation purely from the standpoint of the individual units, there has been a progression of one unit of space simultaneously with each unit of time, as required by the Fundamental Postulates. From the standpoint of the frequency phenomenon as a whole, however, only one unit of space has actually taken part in the action and so far as this phenomenon is concerned, the two units of time are associated with only one unit of space.
The concept of a frequency introduces into our study for the first time a something which can take part in physical phenomena. Heretofore it has been necessary to use indefinite terms such as entities, objects, etc., in developing the general relations but a frequency is a definite entity and can therefore take the place of the indefinite object or entity as the actor on the space-time stage.
Let us now assume that a frequency originates at some point A in space-time. After n units of time have elapsed space and time will have progressed to A+n. The frequency, which must remain stationary in space-time, as it has no mechanism of movement, is carried along with the space-time progression and hence moves outward at unit velocity from the point of origin A. If we now set up a theoretical three-dimensional system of reference points that occupy fixed locations relative to A and do not progress with space-time, we find that the direction of motion of the frequency with reference to our fixed coordinates is indeterminate. Outward from point A may be in any direction relative to our three-dimensional reference system. All directions are equally probable under the circumstances and if a large number of frequencies originate at the same point A the probability relations require that they be distributed equally in all directions. If we observe a source of frequencies from a three-dimensional reference system, we will find that the frequencies are moving away from the source in all directions at unit velocity, the frequencies emitted simultaneously traveling in the form of an expanding spherical surface. This is the phenomenon which we know as radiation.
This radiation is not propagated through a medium. Neither does any effect which may result from the radiation represent “action at a distance.” From a space-time standpoint the frequency is not moving at all. It remains at the point of origin in space-time but that point itself moves, or we might say that it is succeeded by a series of other locations with different space and time coordinates, just as we ordinarily conceive of one instant of time following another.
In order to follow out the program outlined in the introductory chapter and compare the hypothetical universe developed from the two fundamental postulates with the actual physical universe quantitatively as well as qualitatively, it will be necessary to ascertain the relationship between the natural units in which our calculations will be made and the arbitrary units, which have been taken as standards for the customary systems of weights and measures. Most of the accepted units of measurement are secondary; that is, they are derived from other units, but there are a few which are fundamental and the only means by which we can establish the relations between these basic units and the corresponding natural units is to select some readily identified physical magnitude involving each unit and compare the values which are obtained for this magnitude by the two methods. The unit of frequency is an appropriate quantity from which to determine one of these conversion factors.
The value of unit frequency in the c.g.s. system has been calculated from related frequencies. This value, know as Rydberg's fundamental frequency, is 3.2888 x 1015 cycles per second. It will be noted, however, that the cycle per second has been taken as a unit on the assumption that frequency is a function of time only. From the explanation in the foregoing paragraphs it is apparent that a frequency is a velocity, space divided by time, and consequently the natural unit of frequency is one unit of space divided by one unit of time. This is equivalent to one half-cycle per unit of time rather than one full cycle. Expressed in the c.g.s. system the natural unit of frequency is 6.5776 x 1015 half-cycles per second.
With the aid of this natural unit of frequency we are now able to evaluate the natural unit of time. The natural unit of frequency is one natural unit of space per natural unit of time, but the failure to recognize the role of space as a component of frequency hes had the effect of using the natural unit of space in combination with the c.g.s. unit of time as the c.g.s. unit of frequency. In other words, omitting consideration of the space factor in the value of the unit has the same effect as giving it a value of unity. The natural unit of time in c.g.s. units is therefore the reciprocal of the natural unit of frequency or .1520 x 10-15 second.
The natural unit of velocity is the ratio of unit space to unit time. We have fund that radiations travels with unit velocity and that the true velocity of radiation can be obtained by measurement relative to any system of reference, The measured velocity of light in vacuum is evidently of natural unit of velocity in customary units. The c.g.s. value is 2.9989 x 1010 cm/sec.
Since the natural unit of velocity, 2.9989 x 1010 cm/sec, is one natural unit of space per natural unit of time, we multiply this figure by the natural unit of time,
.1520 x 10-15 sec, and obtain the natural unit of space, .4559 x 10-5 cm.
Here we have the explanation of our distorted view of the space-time relations: the reason why space seems so much more real and understandable to us than time. The region of the universe is which human activities are centered is displaced far over on the time side of the neutral axis and hence we are dealing with relatively large time magnitudes and relatively small space magnitudes. As a result we get a close-up view of space and a distant view of time.
The common units of space and time are not directly comparable since they were set up independently without any idea that there was a definite relationship between the two phenomena, however their practical utility depends on their being of the same order of magnitude with respect to human sensation. Because they are designed to be useful the centimeter and the second or any similar pair of practical unit of space and time are approximately equal from the human standpoint; that is, they are about equally distant from the threshold of sensation. But the second, the unit of time which to us is of the same order of magnitude as the centimeter, is actually 3 x 1010 times as large. No wonder time seems elusive and mysterious compared to space when time phenomena must be ten billion times greater than space phenomena in order to make them equally perceptible to us. This enormous difference in our ability to recognize the same natural magnitudes is obviously the reason why we fail to credit time with the properties the we distinguish readily in space.
We have here a difference comparable to looking at a forest first from a distance of a few yards and then from an airplane several miles up. From the close-up view-point we able to distinguish the details: the kind of trees, their size, spacing, etc. Furthermore it is quite apparent that the forest is three-dimensional. On the other hand we learn nothing at all about the extent or shape of the wooded area. From the plane the latter information is ascertained but we can gain no knowledge about these details which were so easily observed from the first vantage point. Here we are even be able to recognize more than one dimension.
Form our position in space-time far over in the time direction we can get a close-time view of space, enabling us to recognize details such as the multiple dimensions, but or field of vision ia too narrow to bring out the characteristics of space in the aggregate. Our view of time from across on the other side of the universe discloses the major features such as the continuous progression but furnishes no details.
Lets us now return to a further consideration itself as radiation the frequency may require a rotational motion, in which case it gives rise to an entirely different character of phenomena and we are justified in considering it as having become an entity of a different kind. These new effect, however, are not due to any differences in the motion itself; all motion in space-time is governed by the same laws. The result entirely from the directional characteristic of rotation.
From a translatory standpoint the net result of a rotational cycle at unit velocity is zero. Since both time and space are directional, the path of rotation is curved in time as well as in space and when the cycle complete the rotating point has returned to the same location in space. Progress in any particular direction has been offset by an equal amount of progress in the revers direction, whit a resultant of zero both in space and in time.
This principle may be further extended by the observation that the path followed in motion from point A to point B has no bearing on the final result, as long as unit velocity is maintained throughout. It is immaterial whether the motion is entirely in translation, entirely in rotation, or is combination of the two. Any changes in space direction are exactly paralleled by corresponding changes in time direction and when point B is reached in space it is also reached in time.The essence of the situation is again the fact that unit velocity is a state of rest in the space-time universe, in rotation equally as well as in translation.
When rotational velocity differs from unity; that is, when a rotational displacement exists, there is a translatory as well as a rotational effect inasmuch as the rotational velocity is is always directed tangentially. The rotation may assume either of two directions: clockwise or counterclockwise, according to the usual terminology. One of these directions is obviously the direction space-time progression and the other it therefore opposite to the progression. A net rotation in the direction of the space-time progression is impossible since this, Together with the progression itself would mean a velocity greater than unity and, as we have found in our consideration of translatory motion, the result would be an oscillation. The independent rotation must therefore be in the direction opposite to the space-time progression.
Let consider a frequency A which has rotation with respect to reference point B actual in magnitude but opposite in direction to the space-time progression. We will also assume for present purposes that A and B are so located that the space-time progression is inward, tending to cause these two points to approach each other. (The factor influencing the direction of the space-time progression will be discussed later). Here we have a conflict. The rotational motion tends to cause A and B to move outward away from each other. This balances the inward space-time progression and as a result there is no net change of position in either direction.
In this illustration it is quite clear that both motions are actually taking place and that the apparent lack of movement is due to one motion cancelling the effect of the other. For many purposes, however, it will be convenient to regard the potential motion in each direction as having been suppressed by the potential motion in the opposite direction. Looking at the situation from this standpoint each of the potential velocities is a tendency to cause motion rather than a actual motion. Here we have concept of force: that which would cause motion if not restrained by opposing forces.
Because of the important role played by force in the physical universe it is desirable to establish definite mathematical relations between this and related quantities before proceeding farther.
From the fundamental entity space-time and its reciprocal forms space and time we have derived velocity: the ratio of space to time. To these we may now add acceleration which will be defined as the rate of change of velocity.
| a = v / t = s / t² |
For more rigorous mathematical treatment both velocity and acceleration should be set forth as differentials:
| v = ds / dt |
| a = dv / dt = d²s / dt² |
The natural unit of acceleration is the natural unit of velocity divided by the natural unit of time. In the c.g.s. system it is
| 2.9989 x 1010 cm/sec | |
| ————————– | = 1.97 x 1026 cm/sec² |
| .1520 x 10-15 sec |
in order to complete the coverage of the velocity group it should be noted since both space and time exist in three dimensions, velocity can also be two-dimensional or three-dimensional. We therefore compute the natural unit of two-dimensional velocity.
| v² = s² / t² = (2.9989 x 1010 cm/sec)² = 9 x 1020 cm²/sec² |
and natural unit of three-dimensional velocity
| v³ = s³ / t³ = (2.9989 x 1010 cm/sec)³ = 9 x 1030 cm³/sec³ |
Now were are comforted with a new concept, that of force, and the immediate problem is to relate it to the velocity group from which it differs in important respect. We find that one set of conditions existing in the system under consideration would normally result in velocity in a particular direction. Another set of conditions existing simultaneously calls for velocity in some other direction. In the kind of a universe which we have postulated both motions cannot manifest them-selves by corresponding changes in actual position. To some extent, therefore, there must be a substitution of tendency to move for actual motion: a substitution of force for velocity.
One fact that stands out clearly in this preliminary consideration is that a force cannot exist alone. Force comes into being only when motion is prevented and it exist as force only as long as the impediment persists. When the impediment is removed the force is transformed into motion.
Now let us take a look at the nature of thus impediment: the something that resist the efforts of force to cause motion. It must, of course, be some function of x velocity, since the tendency to move in a contrary direction in the basis of the conflict that brings force into existence. On the other hand it is diametrically opposite to velocity in character since velocity is a measure of motion whereas we are now dealing with the capacity to resist being moved. A further characteristic of this entity is that it must be three-dimensional as there would be no impediment to the space time progression in any vacant dimension that might exist.
Taking all of these points into consideration we find that we have a picture of an entity which has the properties of the reciprocal of three-dimensional velocity. We will call this entity mass.
The natural unit of mass is equal to the cube of unit time divided by the unit cube of unit space.
| m = t³ / s³ |
In the c.g.s. system the unit can be evaluated as follows:
| (.1520 x 10-15 sec)³ | |
| ———————— | = 3.7 x 10-32 sec³/cm³ |
| (.4559 x 10-5 cm)³ |
This unfamiliar (but convenient) expression can be converted to any desired scale of mass by dividing by the appropriate gravitational constant. The measured value of this constant in common units is simply the ratio of the natural unit of mass to the arbitrary unit of the system of measurement and it is the third of the measured quantities which we will use as a basis for the conversion factor that are needed to express the calculated magnitudes in terms of common unit. In the c.g.s. system this gravitational constant has the value
6.658 x 10-8 and unit mass becomes
| 3.7 x 10-32 | |
| ————— | = .556 x 10-24 grams |
| 6.658 x 10-8 |
This is approximately one-third of the observed mas of the smallest unit of matte, the Hydrogen atom. The exact relation of the Hydrogen mass to the natural unit will be developed later in the study.
We are now in a position to define force with more precision. Since mass is the entity to which the force is applied and acceleration is the rate of change of velocity, the effect of a force, which we may consider to be a reflection of its intensity, is measured by the product of the two.
| F = ma |
Breaking these quantities down into thier component parts we have
| F = t³ / s³ x s / t² = t / s² |
This indicates that force is the analogue of acceleration, the form of the fundamental equation being the same whit time and space interchanged. It should be noted, however, that these two entities do not stand in reciprocal relation to each other as do time and space, mass and three-dimensional velocity, and other pairs of physical quantities which will be studies later.
The natural unit of force is unit time divided be the square of unit space. In c.g.s. unit it is
| .1520 x 10-15 sec | |
| ——————— | = 7.29 x 10-6 sec/cm² |
| (.4559 x 10-5 cm)² |
Again dividing by the gravitational constant
| 7.29 x 10-6 | |
| ————— | = 109.5 dynes |
| 6.658 x 10-8 |
An interesting point disclosed by the foregoing discussion is that force is actually simpler from a dimensional standpoint than mass, involving only two dimensions of space and one of time, whereas mass involves three dimensions of each. This suggests a further dimensional simplification on to yield t/s the reciprocal of velocity, which could logically be expected, on the basis of the facts already developed, to be a fundamental quantity of major significance in physical relation.
This expectation is very definitely borne out. To obtain the quantity t/s we must multiply force by distance. But force time distance is the expression for work or energy.
| E = W = Fs |
Energy then is, the reciprocal of velocity. Where motion is not impeded the space-time displacement manifests itself as velocity; where an impediment exist it manifests itself as energy. We recognize two general forms of energy: potential energy, which is simple impeded motion, and kinetic energy, which is velocity of a mass. The latter. although it is a velocity, is an inverse velocity; that is, velocity of a (three-dimensional) velocity, and it therefore has the dimensions of energy, as we can see if we express both mass and the square of velocity in space-time terms and multiply the two.
| t³ / s³ x s² / t² = t / s |
On this basis kinetic energy can be expressed as **, the factor ½ being a mathematical consequence of the integration process.
The natural unity of energy is one unit of time divided by one unit of space. In c.g.s.units it is **
| .1520 x 10-15 sec | |
| ——————— | = .333 x 10-10 sec/cm |
| .4559 x 10-5 cm |
Dividing by the gravitational constant
| .333 x 10-10 | |
| ————— | = 5.0 x 10-4 ergs |
| 6.658 x 10-8 |
Another basic quantity which should be considered at this time is momentum, the product of mass and velocity. Breaking this expression down into space-time therms we have
| M = mv = t³ / s³ x s / t = t² / s² |
which shows that momentum is the second power of energy, just as mass is the third power. The natural unit of momentum is the square of unit time divided by the square of unit space.
| (.1520 x 10-15 sec)² | |
| ———————– | = .111 x 10-20 sec²/cm² |
| (.4559 x 10-5 cm)² |
Again dividing by the gravitational constant
| .111 x 10-20 | |
| ————— | = 1.665 x 10-14 gm cm/sec |
| 6.658 x 10-8 |
Closely related to momentum is impulse, the product of force and time. Here again we have the second power energy.
| Ft = t / s² x t = t² / s² |
The natural unit of impulse is therefore the same as the natural unit of momentum.
In the foregoing discussion it has been established that mass and the fundamental quantities associated with mass constitute a family group whose relations to time are parallel to the relations which the corresponding members of the velocity group bear to space. To summarize the situation the following tabulation has been prepared.
|
s-t space-time
|
|||
| s, s², s³ | space | t, t², t³ | time |
| s / t | velocity | t / s | enrgy |
| s / t² | acceleration | t / s² | force |
| s² / t² | two-dimensional velocity | t² / s² | momentum |
| s³ / t³ | three-dimensional velocity | t³ / s³ | mass |
The relations treated in the foregoing discussion form the basic for Newton’s celebrated Laws of Motion. The first and second laws are derived directly from the expresion
F = ma and can be stated as follows:
First Law Motion continues unchanged in velocity and direction indefinitely unless acted upon be an external force.
Second Laws Change of moiton is proprtional to the impressed force and takes place on the direction of the force.
For the first law we let F = 0 and we then find that a must also equal 0. A zero rate of change is, of course, no change at allan dthe motion must therefore continue uniformly. This applies to direction as well as to the scalar magnitude of the velocity since accelration is a vector quantity. This first law is often expressed in a menner which draws a distinction between bodies at rest and bodies in motion, a distinction which serves no useful purpose as a body at rest is merely in the limiting condition of motion where the velocity is zero.
The second law *****. This equation also holds good in vector as well as scalar from, hence it applies to both magnitude and direction.
The third law is a statement of the General Reaction Law as it applies to this particular field.
Third Law Every action is accompanied by an equal and opposite reaction.
Analogous to the Third Law of Motion which is an application of the General Reaction Law to a limited field we have the various Conservation Laws which are applications of the General Conversation Law to limited fields. These subsidiary laws may be summed up in one.
Dimensional Conservation Law The General Conservation Law applies to each dimension individually except to the extent that dimensional changes occur.
This is a mere truisum but it leads to the most useful expression of the General Conservation Law as it means that the total space-time displacement in dimensions canot be altered by any process within the physical universe except one that cause transfers from one dimension to another. In one dimension this is the familiar Law of Conservation of Energy, in two dimensions it is the Law of Conservation of Momentum, and in three dimensions it is the Law of Conservation of Mass.
While it has been neccesary to qualify the Dimensional Conversation Law by a significant reservation, this law is nevertheless one of great practical usefulness at its several forms are valid troughout the entire range of ordinary human experience. Only in axceptional situations does the posibility of a dimensional change enter the picture. The outstanding instance in which such a change does take place is the transformation of mass into energy, a process which involveles a transition from t³ / s³ to t / s.
From this relation it is evident that one natural unit of enrgy will be released for each natural unit of mass converted. Owing to the great disparity in size between the two units from our one-sided human viewpoint, however, the amount of energy relased appears to be extremely large inpropoortion to the mass involed. The quantitative aspects of this transition will be examined in a subscequent chapter after the property of mass has been studied in more detail.
