CHAPTER 11
Thermoelectric Properties
As brought out in Chapter 9, the equivalent space in which the thermal motion of the atoms of matter takes place contains a concentration of electrons, the magnitude of which is determined, in the first instance, by factors that are independent of the thermal motion. In the thermal process the atoms move through the electron space as well as through the equivalent of extension space. Where the net time displacement of the atoms of matter provides a time continuum in which the electrons (units of space) can move, a portion of the atomic motion is communicated to the electrons. The thermal motion in the time region environment therefore eventually arrives at an equilibrium between motion of matter through space and motion of space (electrons) through matter.
It should be noted particularly that the motion of the electrons through the matter is a part of the thermal motion, not something separate. A mass m attains a certain temperature T when the effective energy of the thermal motion reaches the corresponding level. It is immaterial from this standpoint whether the energy is that of motion of mass through equivalent space, or motion of space (electrons) through matter, or a combination of the two. In previous discussions of the hypothesis that metallic conduction of heat is due to the movement of electrons, the objection has been raised that there is no indication of any increment in the specific heat due to the thermal energy of the electrons. The development of the Reciprocal System of theory has not only provided a firm theoretical basis for what was previously no more than a hypothesis—the electronic nature of the conduction process—but has also supplied the answer to this objection. The electron movement has no effect on the specific heat because it is not an addition to the thermal motion of the atoms; it is an integral part of the combination motion that determines the magnitude of that specific heat.
Because the factors determining the electron capture from and loss to the environment are independent of the nature of the matter and the amount of thermal motion, the equilibrium concentration is the same in any isolated conductor, irrespective of the material of which the conductor is composed, the temperature, or the pressure. All of these factors do, however, enter into the determination of the thermal energy per electron. Like the gas pressure in a closed container, which depends on the number of molecules and the average energy per molecule, the electric voltage within an isolated conductor is determined by the number of electrons and the average energy per electron. In such a isolated conductor the electron concentration is uniform. The electric voltage is therefore proportional to the thermal energy per electron.
The energy level at which the electrons are in thermal equilibrium with the atoms of a conductor depends on the material of which the conductor is composed. If two conductors of dissimilar composition, copper and zinc, let us say, are brought into contact, the difference in the electron energy level will manifest itself as a voltage differential. A flow of electrons will take place from the conductor with the higher (more negative) voltage, the zinc, to the copper until enough electrons have been transferred to bring the two conductors to the same voltage. What then exists is an equilibrium between a smaller number of relatively high energy electrons in the zinc and a greater number of relatively low energy electrons in the copper.
In this example it is assumed that the voltages in the conductors are allowed to reach an equilibrium. Some more interesting and significant effects are produced where equilibrium is not established. For instance, a continuing current may be passed through the two conductors. If the electron flow is from the zinc to the copper, the electrons leave the zinc with the relatively high voltage that prevails in that conductor. In this case the lower voltage of the electrons in the copper conductor cannot be counterbalanced by an increase in the electron concentration, as all of the electrons that enter the copper under steady flow conditions pass on through. The incoming electrons therefore lose a portion of their energy content in the process of conforming to the new environment. The difference is given up as heat, and the temperature in the vicinity of the zinc-copper junction increases. If the section of the conductor under consideration is part of a circuit in which the electrons return to the zinc, this process is reversed at the copper-zinc junction. Here the energy level of the incoming electrons rises to conform with the higher voltage of the zinc, and heat is absorbed from the environment to provide the electron energy increment. This phenomenon is known as the Peltier effect.
In this Peltier effect a flow of current causes a difference between the temperatures at the two junctions. The Seebeck effect is the inverse process. Here a difference in temperature between the two junctions causes a current to flow through the circuit. At the heated junction the increase in thermal energy raises the voltage of the high energy conductor, the zinc, more than that of the low energy conductor, the copper, because the size of the increment is proportional to the total energy. A current therefore flows from the zinc into the copper, and on to the low temperature junction. The result at this junction is the same as in the Peltier effect. The net result is therefore a transfer of heat from the hot junction to the cold junction.
Throughout the discussion in this volume, the term “electric current” refers to the movement of uncharged electrons through conductors, and the term “higher voltage” refers to a greater force, t/s2, due to a greater concentration of electrons or its equivalent in a greater energy per electron. This electron flow is opposite to the conventional, arbitrarily assigned, “direction of current flow” utilized in most of the literature on current electricity. Ordinarily the findings of this work have been expressed in the customary terms of reference, even though in some cases those findings suggest that an improvement in terminology would be in order. In the present instance, however, it does not appear that any useful purpose would be served by incorporating an unfortunate mistake into an explanation whose primary purpose is to clarify relationships that have been confused by mistakes of other kinds.
A third thermoelectric phenomenon is the Thomson effect, which is produced when a current is passed through a conductor in which a temperature gradient exists. The result is a transfer of heat either with or against the temperature gradient. Here the electron energy in the warm section of the conductor is either greater or less than that in the cool section, depending on the thermoelectric characteristics of the conductor material. Let us consider the case in which the energy is greater in the warm section. The electrons that are in thermal equilibrium with the thermally moving matter in this section have a relatively high energy content. These energetic electrons are carried by the current flow to the cool section of the conductor. Here they must lose energy in order to arrive at a thermal equilibrium with the relatively cold matter of the conductor, and they give up heat to the environment. If the current is reversed, the low energy electrons from the cool section travel to the warm section, where they absorb energy from the environment to attain thermal equilibrium. Both of these processes operate in reverse if the material of the conductor is one of the class of substances in which the effective voltage decreases with an increase in the temperature. There are also some substances in which the response of the voltage to a temperature increment changes direction at some specific temperature level. A similar reversal of the Thomson effect occurs whenever a change of this kind takes place.
The quantitative measure of capability to produce the thermoelectric effects is the thermoelectric power of the various conductor materials. This is the electric voltage, expressed either relative to some reference substance, usually lead, or as an absolute value measured against a superconducting material. Neither the theoretical study nor the experimental measurements are far enough advanced to make a quantitative comparison of theory with experimental results feasible at this time, but some of the general considerations that are involved in the quantitative determination can be deduced from theoretical premises.
The basic difference between the thermal motion of the electrons and that of the atoms of matter is in the location of the initial level, or zero point. The zero for the thermal motion of the atoms is the equilibrium condition, in which the atom is stationary in a three-dimensional coordinate system of reference because the motion imparted to it by the progression of the natural reference system is counterbalanced by the oppositely directed gravitational motion. On the other hand, the zero for the thermal motion of the electrons, the magnitude of the motion of the electrons in the absence of thermal motion, is the natural zero, which, in the context of the stationary reference system, is unit speed, the speed of light. The measure of the energy of the electron motion in matter is the deviation of the speed upward or downward from this unit level.
The fact that the zero energy levels of the positive and negative electron motion are coincident explains why each thermoelectric effect is a single phenomenon in which the zero level is merely a point in a continuous succession of magnitudes, rather than a discontinuous phenomenon such as the resistance to current flow. The difference between a small positive electron speed and a small negative electron speed is itself relatively small, and within the limits of what can be accomplished by a change in the conditions to which the conductor is subject. Such a change in conditions may therefore reverse the motion. But a substance that is a conductor in one temperature or pressure range does not become an insulator in another range, because the positive zero is the equivalent of the negative infinity, rather than the negative zero, and in application to the atomic motion. there is, as a consequence, an immense gap between a small positive thermal speed and a small negative speed.
The status of the electron motion as positive or negative is determined by the position that the interacting atom occupies in its rotational group, in the same manner as the effective electric displacement of the atom. Each of these rotational groups consists of two divisions that are positive from the atomic standpoint, followed by two negative divisions. But since the electron is a single rotating system, instead of a double system of the atomic type, the various subdivisions of the atomic series are reduced to half size in application to the electrons. The reversals from positive to negative therefore occur at every divisional boundary in electronic processes, rather than at every second division.
Identification of individual elements as positive or negative from the thermoelectric standpoint is necessarily subject to some qualifications because, as previously mentioned, some elements are positive in one temperature range and negative in another, but a reasonably good test of the theoretical conclusions can be accomplished by comparing the sign of the thermoelectric power as observed at zero degrees C with the divisional status of the elements for which thermoelectric data are available in one of the recent compilations. Table 27 presents such a comparison, omitting the Division I elements of displacements 1 and 2.
Table 27—Thermoelectric Power
| Division | |||||
|---|---|---|---|---|---|
| I | II | III | IV | ||
| Al+ | Co- | Cu+ | W+ | Si- | |
| Ce+ | Fe- | Zn+ | Ir+ | Pb- | |
| Ni- | Ge+ | Pt- | Bi- | ||
| Mo+ | Ag+ | Au+ | |||
| Pd- | Cd+ | Hg- | |||
| In+ | Tl+ | ||||
| Sn+ | |||||
The reason for the omissions from the tabulation is that the first two Division I elements of each rotational group follow a distinctive pattern of their own. In these elements the factor controlling the thermoelectric power is the magnetic rotational displacement, rather than the electric displacement. Because of the single rotation of the electron, the range of magnetic displacements from 1-1 to 4-4 becomes two divisions, with a reversal of sign at the boundaries. For reasons of symmetry, the interior section from 2-2 to 3-3 constitutes one division, in which the displacement one elements, sodium, potassium, and rubidium, have negative thermoelectric voltages. The corresponding members of the outer groups, lithium and cesium, have positive voltages. The displacement two elements may follow either the magnetic or the electric pattern. One of those included in the reference tabulation, calcium, has the same negative voltage as its neighbor, potassium, but magnesium, the corresponding member of the next lower group, takes the positive voltage of the higher Division I elements.
While the theoretical development that is being described in this work has not yet been extended to the quantitative aspects of the thermoelectric effects thus far discussed, it is of interest to note that the relation of the thermoelectric power to temperature has many of the characteristics that we encountered in our previous examination of the response of other properties of matter to temperature changes. This is well illustrated in Figure 16, which shows the relation between temperature and the absolute thermoelectric power of platinum. Without the captions it would be difficult to distinguish this diagram from one applicable to thermal expansion, or to the specific heat of an element of one of the lower groups. This is no accident. The curves look alike because the same basic factors are applicable in all of these cases.
Figure 16: Absolute Thermoelectric Power—Platinum
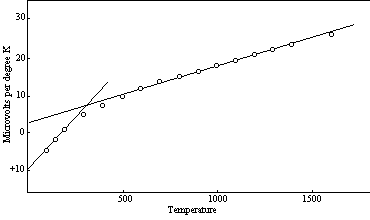
In the platinum curve the initial level is positive and the increments due to higher temperature are negative. This behavior is reversed in such elements as tungsten, which has a negative initial level and positive temperature increments up to a temperature of about 1400 K. Above this temperature there is a downward trend. This downward portion of the curve (linear, as usual) is the second segment. At the present stage of the theoretical development it appears probable that a general rule is involved here; that is, the second segment of each curve, the multi-unit segment, is directed toward more negative values, irrespective of the direction of the first (single-unit) segment.
Another thermoelectric effect is the conduction of heat. This is a process that is more important from a practical standpoint than those effects that were considered earlier, and it has therefore been given more attention in the present early stage of the development of the theory of the universe of motion. Although the examination of the subject was a somewhat incidental feature of the review of electric current phenomena undertaken in preparation for the new edition of this work, it has produced a fairly complete picture of the heat conductivity of the principal class of conducting metals, together with a general idea of the manner in which other elements deviate from the general pattern. It was possible to achieve these results in the limited time available because, as it turned out, the metallic conduction of heat is not a complex process, involving difficult concepts such as phonons, orbitals, relaxation processes, electron scattering, and so on, as seen by conventional physics, but a very simple process, capable of being defined by equally simple mathematics, closely related to the mathematical relations governing purely mechanical processes.
In the first situation discussed in this chapter, that in which two previously isolated conductors of different composition are brought into contact, the electron energies in the two conductors are necessarily unequal. As brought out there, the contact results in the establishment of an equilibrium between a larger number of less energetic electrons in one conductor and a smaller number of more energetic electrons in the other. Such an equilibrium cannot be established between two sections of a homogeneous conductor because in this case there is no influence that requires either the individual electron energy or the electron concentration to take different values in different locations. If the environmental conditions are uniform, both the energy distribution and the electron concentration attain uniformity throughout the conductor.
However, if one end of a conductor composed of a material such as iron is heated, the energy content of the electrons at that location is increased, and a force differential is generated. Under the influence of the force gradient some of the hot electrons move toward the cold end of the conductor. At that end the newly arrived electrons give up heat in the process of reaching a thermal equilibrium with the atomic motion, and join the concentration of cold electrons previously existing at this location. The resulting higher electron pressure causes a flow of cold electrons back toward the hot end of the conductor. None of the characteristic electrical effects are produced in this process, because the two oppositely directed electron flows are equal in magnitude, and the effects produced by one current are cancelled by those produced by the other. The only observable result is a transfer of heat from the hot end of the conductor to the cold end.
It should be noted that no electrostatic potential difference is involved in either of these current flows. This is one of the obstacles in the way of a simple explanation of heat conduction in the context of conventional physical theory, where electric currents are assumed to result from differences in potential. As explained in Chapter 9, our finding is that all of the forces causing flow of current in the conductor under consideration, that due to the excess energy of the hot electrons, that due to the increased concentration of electrons at the cold end, and that due to electric voltage in general, are forces of a mechanical type, not electrostatic forces.
If the material of the conductor is a substance such as copper in which the voltage decreases (becomes less negative) as the temperature rises, the same result is produced in an inverse manner. Here the effective energy of the electrons at the hot end of the conductor is lower than that of the cold electrons. A flow of cold electrons into the hot region therefore takes place. These electrons absorb heat from the environment to attain thermal equilibrium with the matter of the conductor. The resulting increased concentration of hot electrons is then relieved by a flow of some of these electrons back toward the cold end of the conductor. Here, again, the two oppositely directed electron flows produce no net electrical effects.
The conduction of heat in metals by movement of electrons is essentially the same process as the convection of heat by movement of gas or liquid molecules. In a closed system, energetic molecules from a hot region move toward a cold region, while a parallel flow carries an equal number of cold molecules back to the hot region. There is only one significant difference between the two heat transfer processes. Because the fluid molecules are subject to a gravitational effect, heat transfer by convection is relatively rapid if it is assisted by a thermally caused difference in density, whereas it is much slower if the diffusion of the hot molecules operates against the gravitational force.
The quantitative measure of the ability of the electron movement to conduct heat is known as the thermal conductivity. Its magnitude is determined primarily (perhaps entirely) by the effective specific heat and the temperature coefficient of resistivity, both of which are inversely related to the conductivity. There is a possibility that it may also be affected to a minor degree by some other influences not yet identified, but in any event, all of the modifying influences other than the specific heat are independent of the temperature, within the range of accuracy of the measurements of the thermal conductivity, and they can be combined into one constant value for each substance. The thermal conductivity of the substance is then this constant divided by the effective specific heat:
|
Thermal conductivity = k/cp |
(11-1) |
|
As we saw in the earlier chapters, the specific heat of the conductor materials follows a straight line relation to the temperature in the upper portion of the temperature range of the solid state, and the resistance is linearly related to the temperature at all points. At these higher temperatures, therefore, there is a constant relation between the thermal conductivity and the electrical conductivity (the reciprocal of the resistivity). This relation is known as the Wiedemann-Franz law.
The relation expressed in this law breaks down at the lower temperatures, as soon as the specific heat drops below the original straight line. However, the failure of the relation does not occur as soon as would be expected from the normal specific heats of the metals, most of which begin to drop away from the upper linear segment of the curve in the neighborhood of room temperature. The reason for the extension of the high temperature linear relation to a lower temperature in application to thermal conductivity is that the specific heat under the conditions applicable to thermal conduction is not subject to all of the limitations that apply to the transmission of thermal energy by contact between atoms of matter. Instead of going through some intermediate steps, as in the measured specific heats, the effective specific heat in thermal conduction continues on the high temperature basis down to the point where multi-unit motion is no longer possible, and a transition to a single unit basis is mandatory.
The temperature designated as T0 in the previous discussion, the point at which the specific heat curve reaches the zero level, is the same in thermal conduction as in the atomic contacts, but in the interaction between the electrons and the atoms the single rotating system of the electron adds one half unit to the one unit initial level of the double system of the atom. The initial level of the modified specific heat curve is therefore 1½ units (-1.98) instead of the usual one unit (-1.32). This makes the slope of the curve somewhat steeper than that of the initial segment of the normal specific heat curve defined in Chapter 5.
The deviation of the thermal conductivity from the constant relation expressed by the Wiedemann-Franz law is the problem with which any theory of thermal conductivity has to deal, and since the explanation derived from the Reciprocal System of theory attributes this deviation to the specific heat pattern, the best way to demonstrate the validity of the explanation appears to be to work backward from the measured thermal conductivities (reference 21), calculate the corresponding theoretical specific heats from equation 11-1, and then compare these calculated specific heats with the theoretical pattern just described.
Figure 17: Effective Specific Heat in Thermal Conductivity
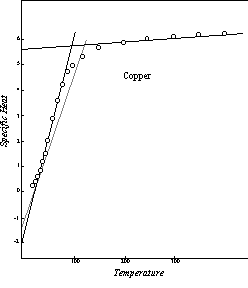
Figure 17 is a comparison of this kind for the element copper, for which the numerical coefficient of equation 11-1 is 24.0, where thermal conductivities are expressed in watts cm-2 deg-1. The solid lines in this diagram represent the specific heat curve applicable to the thermal conductivity of copper, as defined in the preceding discussion. For comparison, the first segment of the normal specific heat curve of this element is shown as a dashed line. As in the illustrations of specific heat curves in the preceding chapters, the high temperature extension of the upper segment of the curve is omitted in order to make it possible to show the significant features of the curve more clearly. As the diagram indicates, the specific heats calculated from the measured thermal conductivities follow the theoretical lines within the range of the probable experimental errors, except at the lower and upper ends of the first segment, where transition curves of the usual kind reflect the deviation of the specific heat of the aggregate from that of the individual atoms.
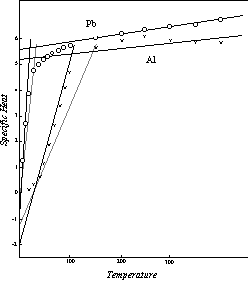
Similar data for lead and aluminum are presented in Figure 18.
Figure 18: Effective Specific Heat in Thermal Conductivity
The pattern followed by the three elements thus far considered may be regarded as the regular behavior, the one to which the largest number of the elements conform. No full scale investigation of the deviations from this basic pattern has yet been undertaken, but an idea of the nature of these deviations can be gained from an examination of the effective specific heat of chromium, Figure 19. Here the specific heat and temperature values in the low temperature range have only half the usual magnitude. The negative initial specific heat level is -1.00 rather than -2.00, the temperature of zero specific heat is 16 K rather than 32 K, and the initial level of the upper segment of the curve is 2.62 instead of 5.23. But this upper segment of the modified curve intersects the upper segment of the normal curve at the Neel point, 311 K, and above this temperature the effective specific heat of chromium in thermal conductivity follows the regular specific heat pattern as defined in Chapter 5.
Figure 19: Effective Specific Heat in Thermal Conductivity
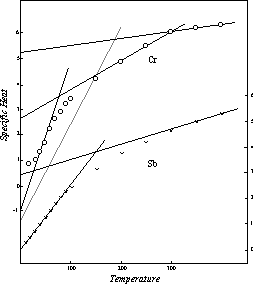
Another kind of deviation from the regular pattern is seen in the curve for antimony, also shown in Figure 19. Here the initial level of the first segment is zero instead of the usual negative value. The initial level of the second segment is the half sized value 2.62. Antimony thus combines the two types of deviation that have been mentioned.
As indicated earlier, it has not yet been determined whether any factors other than the resistivity coefficient enter into the constant k of equation 11-1. Resolution of this issue is complicated by the wide margin of uncertainty in the thermal conductivity measurements. The authors of the compilation from which the data used in this work were taken estimate that these values are correct only to within 5 to 10 percent in the greater part of the temperature range, with some uncertainties as high as 15 percent. However, the agreement between the plotted points in Figures 17, 18 and 19, and the corresponding theoretical curves shows that most of the data represented in these diagrams are more accurate than the foregoing estimates would indicate, except for the aluminum values in the range from 200 to 300º K.
In any event, we find that for the majority of the elements included in our preliminary examination, the product of the empirical value of the factor k in equation 11-1 and the temperature coefficient of resistivity is between 0.14 and 0.18. Included are the best known and most thoroughly studied elements, copper, iron, aluminum, silver, etc., and a range of k values extending all the way from the 25.8 of silver to 1.1 in antimony. This rather strongly suggests that when all of the disturbing influences such as impurity effects are removed, the empirical factor k in equation 11-1 can be replaced by a purely theoretical value k/r, in which a theoretically derived conversion constant, k, in the neighborhood of 0.15 watts cm-2 deg-1 is divided by a theoretically derived coefficient of resistivity.
The impurity effects that account for much of the uncertainty in the general run of thermal conductivity measurements are still more prominent at very low temperatures. At least on first consideration, the theoretical development appears to indicate that the thermal conductivity should follow the same kind of a probability curve in the region just above zero temperature as the properties discussed in the preceding chapters. In many cases, however, the measurements show a minimum in the conductivity at some very low temperature, with a rising trend below this level. On the other hand, some of the elements that are available in an extremely pure state show little or no effect of this kind, and follow curves similar to those encountered in the same temperature range during the study of other properties. It is not unlikely that this will prove to be the general rule when more specimens are available in a pure enough state. It should be noted that an ordinary high degree of purity is not enough. As the data compilers point out, the thermal conductivities in this very low temperature region are “highly sensitive to small physical and chemical variations of the specimens.”
