CHAPTER 8

Evolution—Globular Cluster Stars

Even though a globular cluster may contain as many as a million stars, it is too small to have any major effect on the structure of a barge spiral galaxy such as ours when a capture takes place. But since this capture occurs practically on our doorstep, we are able, to trace the progress of the clusters into the main body of the galaxy, and to read their history in considerable detail. This process is too stow to be followed observationally, but we can accomplish essentially the same thing by identifying clusters in successively later stages of development, and establishing the order in which the various changes take place.

As brought out in Chapter 3, the globular clusters are being drawn in toward the galaxy from the surrounding space by gravitational forces, and the observed concentration of the clusters thus far located within a sphere that has a radius of about 100,000 light years is merely a geometrical effect. The clusters move “as freely falling bodies attracted by the galactic center” , and they do not participate, to any significant extent, in the rotation of the Galaxy. Thus the observations indicate that the clusters are on the way to capture by the Galaxy.

The increasing strength of the gravitational forces as the clusters approach closer to the Galaxy has a disruptive effect on the positional equilibrium within the clusters. The outer stars tend to be stripped away, and the clusters therefore decrease in size as they approach. Observations reported in Chapter 3 indicate that a cluster loses more than one third of its mass by the time it reaches a position within l0,000 parsecs of the galactic center. In the capture zone, the region in which the structure of the clusters begins to be disrupted, the losses are still greater, and at the time when contact is made with the Galaxy the remaining stars are numbered in the tens of thousands rather than in the original hundreds of thousands. On entry into the rapidly rotating galactic disk still further disintegration occurs, and the globular cluster separates into a number of open clusters. These are relatively small groups, most being in the range from around a dozen to a few hundred stars, although a few have as many as a thousand.

The total mass of a small cluster of this kind is not large enough to produce a gravitational attraction that is equal to the outward progression of the natural reference system, even when augmented by the gravitational effect of the galaxy as a whole The open clusters are therefore expanding at measurable rates. One of the results of this rapid expansion is that the lifetime of these clusters is relatively short. In order to account for the large number of such clusters now in existence, which runs into the thousands—one estimate (reference 96) is 40,000 when due allowance is made for the fact that only a small fraction of the total can be identified from our position in the galaxy, there must be some process in operation that continually replenishes the supply. The astronomers have been unable to find any such process. Like other members of the human race, they are reluctant to admit that they are baffled, so the general tendency at present is to assume that the open clusters must originate by means of the star formation process that they believe is taking place in dense dust clouds. But this explanation simply cannot stand up. If the cohesive forces in these clouds are strong enough to form a cluster they are certainly strong enough to maintain it. The observed expansion thus contradicts the hypothesis of formation near the present cluster sites.

Of course, it is conceivable that some clusters formed under certain favorable conditions might at some later date encounter conditions that would cause them to disintegrate, but all open clusters are disintegrating, and astronomical theory has to explain this fact. No stable stellar aggregate exists in the range between the globular clusters and the multiple star systems. If the issue is squarely faced, it is clear that conditions in the Galaxy are favorable for dissolution of the clusters, whereas the existing clusters must have been formed under conditions favorable for such formation.

Those astronomers who do face the issue recognize that current theory has no satisfactory answer to the problem, notwithstanding the wide range of possibilities that has been explored. Bok and Bok, who discuss the question at some length, conclude that at least some classes of clusters are not being replaced. The most conspicuous clusters, the Pleiades, Hyades, etc., are disintegrating, and these authors say that “there seem to be no others slated to take their place.” Likewise they conclude that the ”open clusters with stars of spectral types A and later… may be a vanishing species.⁹⁷

The obvious answer cannot be ignored completely. Bok and Bok concede that “one might be tempted to think about dismembered globular clusters as possible future Pleiades-like clusters” , but since this conflicts with the prevailing ideas as to the direction of stellar evolution, they resist the temptation, and dismiss the idea as impossible. Here, again, the physicists, assumption as to the nature of the energy generation process must be supported, whatever the cost to astronomy may be. The two considerations that they say “show how impossible this would be” are first, that the spectra changes required in going from globular to Pleiades-like clusters are impossible, and second, that the “rate of evaporation for globular clusters is far too slow.” The first of these objections is simply a reiteration of the upside down evolutionary sequence that the astronomers have adopted to conform to the physicists, assumptions. As already explained, the evolutionary path for all stars is from globular cluster to main sequence, not vice versa. And the globular clusters that fail into the Galaxy do not shrink slowly by evaporation; they are torn apart quickly by the rotating matter of the galactic disk. The piece of information that has been lacking in the astronomers, view of the situation is the existence of an interstellar force equilibrium that gives an aggregate of stars the physical characteristics of a viscous fluid. The entry of the cluster into the galaxy is physically similar to the impact of one fluid aggregate on another. All of the elements of the problem fall into place when it is viewed in the light of the theory of the universe of motion.

The conclusion as to the origin of the open clusters derived from this theory is reinforced by the available data on the properties of these stellar groups. One of these properties is the density of the group. Any gravitationally bound group of stars has a density greater than that of the field of stars in its environment. Inasmuch as the aggregate of stars in the Galaxy has the characteristics of a liquid, a stellar group whose density exceeds the density of the field stars will fall toward the galactic plane. This is a necessary consequence of the gravitational differential, and the descent will take place regardless of the nature of the influences that are responsible for the separation between the field stars, and regardless of whether the clusters fall into the Galaxy, as asserted by the theory of the universe of motion, or originate somewhere within that structure, in accordance with present-day astronomical theory. Even the much looser “associations” participate in this response to the gravitational diffcrential.⁹⁸

Since the clusters are falling objects, those that are higher above the galactic plane are younger, on the average, than those lower down. One of the most conspicuous members of the higher class is M 67, about 440 parsecs above the plane. At the other extreme are objects such as the double cluster in Perseus, which is in the general vicinity of the plane. It follows directly from the relative positions of the two classes that the clusters of the M 67 class are the younger and those of the Perseus class are the older.

This conclusion derived from the relation of position to cluster density is corroborated by direct observation of density changes. Inasmuch as the clusters are expanding, their densities are decreasing with age. While the density of any individual cluster may reflect the particular conditions to which it has been subject, the average density of the clusters of each class should depend mainly on the amount of expansion that has occurred It therefore follows that the clusters with the higher average density are the younger, and those with the lower average density are the older. Studies show that the clusters of the M 67 class have the higher average density.⁹⁹ Hence these are the young clusters, and the clusters of the Perseus class are relatively old—the same conclusion that we reach from a consideration of the positions above the galactic pane. Both of these indications of relative age are observed properties of the clusters, and are independent of the astronomical theory in whose context they are viewed. In this case, then, we have something that is very rare in astronomy: a direct observational indication of the direction of evolution.

Here we have positive proof that the stars of the main sequence are older than the stars of the globular cluster type (the kind of which M 67 is composed). This negates the basic premise on which current theory of stellar evolution is founded. That theory asserts that the stars of the upper main sequence are necessarily young because the supply of hydrogen for production of energy will be exhausted in these stars in a relatively short time. The proof that these stars are not young now turns the argument upside down. The demonstrated fact that they are relatively old stars shows that hydrogen is not the stellar fuel

With the addition of this evidence to the many items previously noted, we now have a positive definition of the direction of evolution of the stars of the globular and open clusters, and by extension, a definition of the direction of stellar evolution in general. In order to see just how this information fits into the theoretical picture, we will now turn to a consideration of the evolution of the stars in the clusters.

Inasmuch as the remains of disintegrated stars and galaxies are scattered throughout all space, and atoms of matter are continually forming in this space from the decay products of the cosmic rays, there is a certain minimum amount of material subject to accretion in any environment in which a star may be located. Immediately after the formation of a globular cluster star by condensation of a portion of a protocluster, this thin diet of primitive material and the atom building that takes place within it, are all that is available for growth, and the evolution of the stellar structure is correspondingly slow. The stars of the globular clusters are therefore in an early stage of development. Aside from a few strays from older systems that have been incorporated during the formation of the cluster, the distant clusters contain only Class I stars: infrared stars, red giants, sub-giants, long-period Class IA variables, and variables of the RR Lyrae and associated types. To these, the clusters closer to the Galaxy add some Class 1B stars of the lower main sequence.

As noted in Chapter 4, the CM diagram provides a picture of the most significant changes that take place in the constituent stars of the globular clusters. The first stage of their evolution, after they become observable in area O of the diagram, is a contraction under the influence of the combined gravitational forces of each star itself and the cluster as a whole. This ends for each star when it reaches gravitational equilibrium on the line BC, the main sequence. Thus the paths OAB and OAC on the CM diagram of M 3 are the routes followed by the stars of this cluster in the continuation of the process by which they originated. The locations along this path represent what we may call evolutionary ages. A star at point B or point C has traveled the entire length of its path OAB or OAC.

Although it is common practice to refer to the pre-stellar aggregate as a dust cloud, it is actually a gas cloud with a small dust content. Thus the physical aspect of the evolution of the newly formed stars is defined by the behavior of an isolated gaseous aggregate subjected to a continuing increase in temperature and pressure under the influence of gravitational forces. Since the matter of the star is above the critical temperature by the time that the pressure reaches significant levels, it has been assumed that the star is gaseous throughout its structure. As expressed in one textbook, “Because the sun (a star) is so hot throughout all its volume, all of its matter must be in the gaseous state.”¹⁰⁰

This statement is valid on the basis of the conventional definition of the gaseous state, in which this state has no density limit, but the investigation upon which this work is based (see Volume II) has shown that this definition leads to some erroneous conclusions. In particular, it leads to the conclusion that all matter above the critical temperature conforms to the gas laws—the general gas equation PV = RT, and its derivative relations. This is not true. In fact, these laws do not apply to matter at all. They apply only to the empty space between the atoms or molecules of the gas. At very low densities the volume of a gas aggregate, as measured, consists almost entirely of empty space, and the gas laws are therefore applicable. As soon as the density increases to the point where the volume occupied by the particles of matter begins to constitute an appreciable proportion of the total, a correction for the deviation of the volume from that of the “ideal gas” (the empty space) must be applied. A further increase in density ultimately brings the aggregate to a critical paint at which the correction becomes the entire volume; that is, the empty space has been completely eliminated. The aggregate is now a condensed gas.

Inasmuch as conventional physics has no theoretically based relations from which to compute the magnitudes of the various properties of gas aggregates at high pressures, and relies on empirical relations, restricted to a relatively low pressure range, for this purpose, the existence of this third condensed state of matter was not detected prior to the development of the theory of the universe of motion. In the light of this theory, however, the existence of this condensed gas state is a necessary consequence of the nature of physical state. In the gaseous state the individual units—atoms or molecules—are separated by more than one unit of space, and are therefore moving freely as independent particles. In the condensed states—solid, liquid, and condensed gas—the separation has been reduced to the (equivalent of less than a unit of space (by the introduction of time). Here the individual particles occupy fixed (solid state) or spatially restricted (liquid and condensed gas) positions in which they are subject to a set of relations quite different from the gas laws. For example, as brought out in Volume II, the volume of a solid aggregate is inversely proportional to the square root of the total pressure, including the internal pressure, rather than inversely proportional to the external pressure as in the gaseous state.

A study of the volumetric relations carried out in the course of the investigation on which this work is based has disclosed that the transition to condensed gas takes place within the temperature and pressure range of much of the experimental work reported in the scientific literature. For instance, application of the theoretical relations to the volumetric data on water at 1000 C indicates that the transition from the gaseous state to the condensed gas state begins at about 600 atm. pressure, and is completed at about 3000 atm. Above this level the condensed gas volume can be computed by means of the relations that apply to the liquid state. The temperatures in the stars are, of course, vastly greater, but so are the pressures, and both the gaseous and condensed gas states exist within the stellar temperature and pressure range, a fact that has an important bearing on the evolutionary pattern of the stars.

One important property shared by all of the condensed states is that an aggregate in any one of these states has a definite surface. This is not true of a gas cloud. Such an aggregate simply thins out with the radial distance until it reaches the density of the surrounding medium. This point is generally recognized in the case of star clusters and galaxies, which are structures of the same kind, differing only in that the constituent units are stars rather than particles. The fact that the dimensions of these objects, as observed, depend on the limiting magnitude reached by the observations is well known, but the corresponding phenomenon in the stars, if it is recognized at all, is not emphasized in the astronomical literature. This is no doubt due, at least in part, to the observational difficulties. The dimensions of the stars of the dust cloud classes can only be observed by means of special techniques of limited applicability (such as interference methods) or under special circumstances (such as in eclipsing variables), and the absence of surfaces has not been evident enough to attract attention. The only star that is readily accessible to observation, the sun, belongs to the other class of stars, those that do have definite surfaces.

The condensation of a dust and gas cloud under the influence of gravitational forces is an equilibrium process, not a static equilibrium like that of the stars on the main sequence, where the variables react in such a way as to maintain constant relations, but a dynamic equilibrium, in which the interactions between the variables maintain a uniform pattern of change in their relations. Consequently, all of the clouds condensing into stars follow the same evolutionary path, differing only in the rate at which they move along that path. At any given stage of the contraction process along the line OA on the CM diagram all stars therefore have the same effective mass and volume (aside from the variations that are responsible for the width of the line), irrespective of the size of the dust clouds from which they are drawing their material.

In this first part of the evolutionary path the continuing condensation of the stellar aggregate is made possible only by the assistance of the gravitational effect of the cluster as a whole, as this early type of star is not a self-gravitating object. As indicated in the earlier discussion, however, the gravitational forces of the star are strengthened as it becomes denser, and at a certain point, designated A on the CM diagram, Figure 3, the star reaches the critical density where it becomes self-gravitating; that is, it is capable of further contraction toward gravitational stability without outside assistance. Beyond the point at which the critical density is reached, the two processes, the original growth process and the self-gravitation, are in competition. The outcome depends on the relative rapidity of the processes.

If the growth of the star has taken place all the way from particle size, without the benefit of any gravitationally stable core, the contents of the parent dust cloud are practically exhausted by the time that the star reaches the critical density at point A. In this event the self-gravitation initiated at A proceeds at a more rapid rate than the growth by accretion. The star then pulls away from its surroundings and moves directly down the diagram along the line AB, the line of constant mass.

If the star did have a pre-existing fragment as a nucleus, growth along the line OAC is able to continue. As noted in Chapter 4, the availability of even a very small fragment as a nucleus for condensation gives a star a big advantage over the majority, which have to start from particles. Because of the much larger amount of dust and gas over which they are able to establish gravitational control, these stars that had the head start are usually able to follow the line AC all the way to point C, or at least to the vicinity of that point. In some cases there is a tendency for the observed paths to bend downward shortly before reaching C, indicating that the material for growth has been exhausted. In other eases the trend in the vicinity of point C is upward. This is no doubt due to accelerated accretion from favorable environments.

Inasmuch as the nature of the process by which the primitive cloud of matter was formed, as described in Chapter 1, produces essentially the same initial conditions in each cluster, the equilibrium conditions are practically the same for all clusters. It follows that the critical points A and C on the line OAC are the same for all of these clusters. This conclusion refers, of course, to the true values, the absolute magnitudes. But the astronomers, evaluation of absolute magnitudes is subject to a considerable degree of uncertainty. For present purposes, therefore, it appears to be advisable to deal with the observed magnitudes, using the observed magnitude at some identifiable location in each diagram as a reference point. The resulting diagram is identical with that which would result from the use of the correct absolute magnitudes, except that the magnitude scale is shifted by an amount that reflects the effect of distance and obscuration.

There are some other factors—chemical composition, for instance—in addition to the evolutionary development, that affect the variables represented on the CM diagram, and these factors, together with the observational uncertainties, result in rather wide evolutionary paths, but aside from these effects, the foregoing theoretical conclusions indicate that the upper sections of all CM diagrams of globular clusters should be identical, to the extent that the evolution of each cluster has progressed.

Figure 9 shows that this theoretical pattern is followed by six of the most prominent globular clusters. The outlined areas in each cluster diagram show the observed star locations. The boundaries of these areas have been located by inspection of diagrams published in the astronomical literature. Greater accuracy is possible, but this would call for an expenditure of time and effort that did not appear to be justified for the purposes of this somewhat preliminary survey of the situation.

The theoretical evolutionary lines, the diagonal lines in the diagrams, are the same for all clusters, except that in each case the reference point determines the magnitude scale. Whatever differences in the lengths and slopes of these lines may exist between the individual diagrams are due to differences in the scales of the original diagrams from which the data were taken. The upper of the three points identified on each line is the reference point. The point corresponding to a B-V color index of 1.4 has been selected as the reference point in most of the CM diagrams in this volume, because it is usually quite clearly defined by the observations, but where the 1.4 location is uncertain some better defined location has been substituted. What the diagrams show is that if the location of the reference point is taken to represent the absolute value of the luminosity, then the points A and B on the line OAC, as previously defined, have the correct theoretical relation to the reference value, within the accuracy of the representation. Some of the evolutionary paths tend to diverge from the theoretical line as they approach the main sequence at point C, but the deviation is within the range of the processes previously mentioned as being applicable in this region.

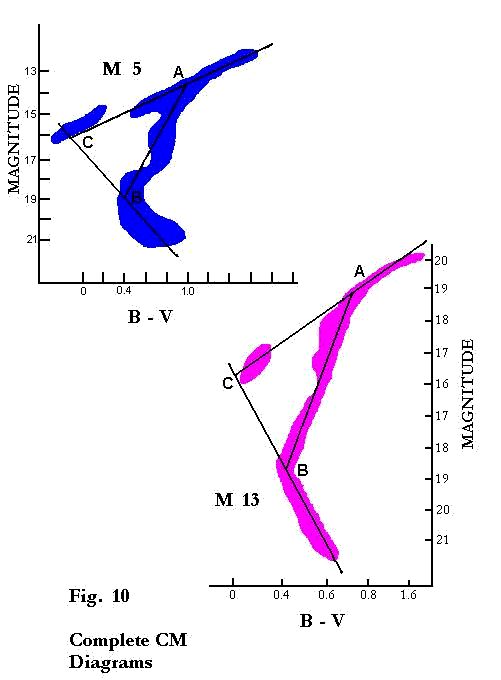
These considerations that apply to the upper section of the diagram, the line OAC, are likewise applicable to the lower sections, the line AB and the relevant portion of the main sequence, which have been identified observationally for only a limited number of clusters. It then follows that when the location of any one point is specified in the manner that has just been described, the M 3 pattern can be applied to a determination of the entire theoretical pattern of any globular cluster. The complete CM diagrams thus obtained for two of the clusters of Figure 9 are shown in Figure 10. These clusters clearly conform to the theoretical pattern.

It is true that there is considerable variability in the line AB, but this is easily understood as a result of the expansion and contraction of the cluster during the travel toward the Galaxy. As explained in Chapter 3, the cluster is subject to substantial loss of stars during its approach, because of differential gravitational effects. These losses alter the equilibrium in the cluster, and tend

to cause density fluctuations. The variations in the cluster density have a corresponding effect on the pressure that is exerted on the individual stars by the gravitational force of the cluster as a whole, thus transmitting the density fluctuations to the stars. If the cluster and its constituent stars are expanding as the stars approach point A, the contraction along the line AB is delayed to some extent, and the evolutionary path is displaced to the left of the line. Then, when the expansion phase of the density cycle is succeeded by a contraction, the path is displaced to the right at some location farther down the line. There may even be another swing to the left before the main sequence is reached. As can be seen in the diagrams, this cyclic effect is at a minimum in M 13, but it shows up clearly in such clusters as M 3 and M 5.

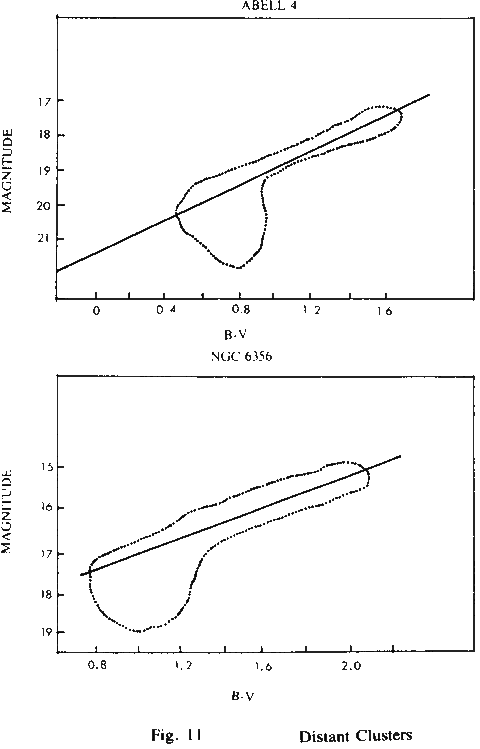
The red giant section OA of the CM diagram of a globular cluster is usually well defined, even where the limiting magnitude to which the observations have been carried cuts off most of the lower portions of the diagram. Since only one observed point is required in order to establish the complete Class l diagram, and any point in this well-defined giant section will serve the purpose, it is not difficult to define the theoretical CM diagram for an ordinary globular cluster. Furthermore, if the observations extend to the main sequence, the accuracy of the diagram thus defined can be verified by the observed positions of the main sequence stars. Thus, as indicated by the diagrams already introduced, there is little question as to the position of the evolutionary paths. Uncertainties arise only in the case of the very distant clusters that are observed with such difficulty that only the most luminous stars can be identified. Even at these distances the diagrams are often well defined. For instance, Figure 11 shows the relation between the theoretical OAC line and the observed locations of the stars of two of the most distant clusters for which data are available. These clusters, NGC 6356 and Abell 4 have uncorrected magnitudes at a B-V color index of. 1.4 of. 16.2 and 18.2 respectively. These compare with l 2.l for M 13 and 10.4 for NGC 6397, the cluster closest to the sun. The luminosity of the most distant of these four clusters is less than that of the closest by a factor of more than a thousand.

A point that should be noted in connection with the evolutionary pattern of the globular clusters is that the difference in luminosity (on the logarithmic scale) between point B and point A, 5.6 magnitudes, is twice the difference between point B. and point C, which is 2.8 magnitudes. The significance of this relation will be discussed in Chapter 11.

Identification of the globular cluster pattern as a fixed relationship provides a simple and potentially accurate method of determining the distances to the clusters. Inasmuch as the theoretical findings indicate that the pattern is identical for all the clusters, it follows that the absolute magnitude corresponding to any specific color index is the same for all. Like the evolutionary pattern itself, we will have to determine this absolute magnitude empirically for the present but once we have it for one cluster, we can apply it

to all clusters. A value of 4.6 at a B-V color index of 0.4 on the main sequence has been selected on the basis of two criteria. First, this agrees with the currently accepted values applicable to the nearest clusters which are presumably the most favorably situated for accurate observation, and second, this value arrives at practically the same average as the observational values given by W. E. Harris for a long fist of clusters.¹⁰¹ These previously reported values from observation should average close to the correct magnitude if there are no systematic errors, even though the error range of the individual values is conceded to be quite wide. The distance moduli (the differences between the absolute and apparent magnitudes) calculated on the 4.6 basis are compared with those given in the tabulation by Harris in Table II. A few distant clusters not listed by Harris are also included. For the benefit of those readers who are not much at home with the astronomers, magnitude system, the distances are expressed in terms of light years in the last column of the table.

The potential accuracy of the method is not fully attained in the present work because of the previously mentioned approximate nature of the process employed in identifying the reference point for each cluster. But even so, more than half of the values calculated on this basis in the course of the present study agree with the values given by Harris within his estimate of the probable error range. Most of the observers, original reports do not specify whether the values shown in their diagrams have been corrected for the reddening due to dust along the line of travel of the radiation. The theoretical distances in the table have been calculated on the assumption that no such correction has been applied to the plotted values. If this is incorrect in any specific case, the calculated distance will be modified accordingly.

The main sequence, as defined by the astronomers,¹⁰² has an absolute magnitude of about 3.8 at a B-V color index of 0.4. This puts it 0.8 magnitudes above the position obtained for the globular clusters from the study of the CM diagrams. The significance of this difference will be discussed later.

The evolutionary age of each cluster is indicated by its position on the CM diagram. The overall range from the earliest to the latest type of star in the cluster remains about the same, but the positions of both the front end of the age sequence, the location of the most advanced stars, and the rear end, the location of the least advanced, move forward. Bart J. Bok comments that the branch of the diagram of the cluster Omega Centauri that is occupied by the red giants “is unusually long” , and also that the data “do not reveal the full extent of the main sequence.”⁸⁷ He attributes the length of the giant branch to a high degree of variability in the metal content. Our analysis shows, however, that both of the features of the diagram that Bok mentions are aspects of the same thing. They indicate that Omega Centauri is not as far advanced from the evolutionary standpoint as a cluster such as M 13, for example. There are stars in Omega Centauri that are earlier (that is, farther to the right in the CM

TABLE II
DISTANCES - GLOBULAR CLUSTERS

Cluster	Reddening	Distance Modulus		Distance (lt. years)
		Harris	This Work
Abell 4			20.2	357,000
Palomar 14			20.0	326,000
NGC 6256			19.2	225,000
Kron 3			18.8	188,000
NGC 6356	0.21	17.07	18.0	130,000
M 14	0.58	16.9	17.7	113,000
Palomar 5			17.2	90,000
NGC 6235	0.38	16.6	16.4	62,000
NGC 6144	0.36	15.6	15.8	47,000
NGC 1851	0.07	15.4	15.8	47,000
NGC 6535	0.36	16.1	15.6	43,000
NGC 6535	0.36	16.1	15.6	43,000
M 79	0.00	15.65	15.3	37,000
NGC 5053	0.03	16.00	15.3	37,500
NGC 288	0.00	14.70	14.9	31,000
M 68	0.03	15.01	14.7	28,000
M 15	0.07	15.26	14.6	27,000
M 3	0.00	15.00	14.6	27,000
M 30	0.01	14.60	14.5	26,000
M 5	0.07	14.51	14.4	26,000
M 2	0.19	14.30	14.3	23,500
Omega Centauri	0.11	13.92	14.3	23,500
47 Tuc.	0.04	13.46	14.2	22,500
M 71	0.28	13.90	14.1	21,500
NGC 3201	0.28	14.15	14.1	21,500
M 13	0.02	14.35	14.1	21,500
M 22	0.35	13.55	13.9	19,700
M 92	0.01	14.50	13.9	19,700
M 55	0.07	14.00	13.9	19,000
M 4	0.01	13.20	13.1	14,300
NGC 6752	0.01	13.20	13.1	13,700
NGC 6397	0.13	13.30	12.3	9,400

diagram) than the earliest stars in M 13, while not enough stars have reached the main sequenced to give this cluster a main sequence population comparable to that of M 13.

The evolutionary age of the matter of which the stars of a cluster are composed is, of course, related to the age of the cluster, but these ages are not coincident. The chronological age of the matter includes not only the time spent in the star cluster stage, but also the time spent in the diffuse stage that precedes condensation into a star. This is subject to considerable variation. Furthermore, there are circumstances under which the evolution of the matter proceeds much faster than the evolution of the cluster. Thus, although the older clusters are, in general, composed of older matter, there is no direct relation. Some examples of accelerated evolution of matter in clusters will be examined in Chapter 9.

The question as to the ages of the globular clusters has received a great deal of attention from the astronomers because they are presumed to have been formed within a relatively short time after the Big Bang in which most astronomers now believe the universe originated. On this basis, as Bok points out in a recent discussion of the subject, the clusters “seem to be the oldest objects in the Milky Way.”⁸³ But it is agreed that the concentration of “metals” (heavy elements) in an astronomical object is an indicator of its age, and as Bok acknowledges, there are differences in the metal content of the clusters that “imperil” the current theory of their formation. Some, particularly those most distant from the galactic center, are relatively metal-poor, while others have substantially greater metal content. Harris and Racine give us this assessment of the situation: “It is plain that the maximum [Fe/H] decreases roughly linearly with log R [distance from the galactic center], even out to about 100 kpc.”¹⁰⁴

Many astronomers are beginning to recognize that this radial dependence of the cluster ages, as indicated by the metal abundances, is inconsistent with present-day astronomical theory. Bok, for example, recognizes that something is wrong here. He states the case in this manner: “The spread of ages for the globular clusters conflicts with current models of how the galaxy evolved.”⁸³

Our finding is that almost all of the conclusions in this area that have been reached on the basis of current astronomical theory are wrong, either in whole or in part. On first consideration it may seem unlikely that errors would be made on such a wholesale scale, but actually this is an inevitable result of the manner in which astronomical conclusions have to be reached under present conditions, where there is no general theoretical structure connecting the various astronomical areas. In the absence of the restraints that would be imposed by such a general structure, wrong theories and wrong interpretations of observations are able to reinforce each other and resist correction In the case now under consideration, a wrong theory of stellar energy generation, a wrong theory of the origin of the universe, and a wrong theory of stellar evolution provide mutual support for each other, and for the wrong interpretation of the place of the globular clusters in the astronomical picture.

Correction of these errors one by one is not feasible, because a change in only one of the erroneous hypotheses introduces obvious contradictions with those that are retained. All of the major errors that are relevant to the point at issue have to be corrected simultaneously in order to arrive at a consistent system of thought. This is the objective of the present work.