CHAPTER 22

Verification

The quasar theory described in Chapter 21 accounts for the major features of these objects: what they are (fast-moving galactic fragments), how they originate (by explosions of massive old galaxies), where their energy comes from (large numbers of supernovae), what gives them their unique characteristics (speeds greater than that of light), and what their ultimate destiny will be (escape into the cosmic sector, the sector of motion in time). These are all necessary consequences of the physical principles of the universe of motion, as developed in the earlier volumes of this work, and the quasars are directly in the main line of the cyclic evolution of matter as described in the preceding pages of this present volume. But in view of the unfamiliar nature of some of the physical principles that are applicable to objects moving at upper range speeds, and the important part that these unfamiliar principles play in the quasar theory, it will be advisable to supply some additional verification of the Validity of that theory by locating some specific situations in which we can compare the predictions of the theory with the results of observation.

The most significant situations of this kind are those in which the predictions of the new theory are unique; that is, those in which the development of the Reciprocal System of theory arrives at conclusions that are totally different from those derived from other sources. Situations that lead to quantitative answers are particularly meaningful. One such item is that there is a specific mathematical relation between the normal recession redshift and the explosion redshift, the increment due to the ultra high speed imparted to the quasar by the galactic explosion. The existence of this fixed relation is due to the fact that the motion generated by the explosion is a scalar motion of the same general nature as the recession, differing only in the number of dimensional units involved. The retarding effect of gravitation is variable, but it applies equally to all units, except as modified by the inter-regional relations. As explained in Chapter 15. where the recession redshift is z, the corresponding explosion redshift is 3.5z^½ (except under some special conditions that will be discussed later). A crucial test of the theory can therefore be accomplished by identifying the relative magnitudes of the two redshift components in a representative number of quasars, and comparing the results with the theoretical values.

As matters now stand, there is no way by which we can separate the observed redshift of an ordinary quasar into its two components, other than by means of the theoretical relation. But because of the manner in which the quasars originate, each of these objects is a member of a three-component group consisting of (1) the galaxy in which the explosion occurred, (2) the quasar, and (3) a radio galaxy. As a result of the reversal of directions at the unit speed level, the radio galaxy is ejected in the spatial direction opposite to that of the motion of the quasar. These two objects are therefore located on opposite sides of the galaxy of origin. All three members of each group occupy adjacent locations in space, and their recession redshifts are approximately equal, differing only by the amounts due to the random motion in space and to the relatively small change of position since the explosion. Disregarding these minor items, a three-component association resulting from a galactic explosion should consist of a central galaxy with redshift z, an ordinary radio galaxy with redshift z, and a quasar with redshift z + 3.5 z^½ In any case where at least one of the associates of a quasar in such a group can be identified, and the redshifts have been measured, we can test the validity of the theoretical relation by computing the value of the quasar redshift that theoretically corresponds to the value z obtained from the associated object at the same spatial location, and comparing it with the observed quasar redshift.

As it happens, Dr. Halton Arp, a prominent American astronomer, has made an intensive search for radio sources associated with galaxies of a “peculiar” nature. Since both the quasar and the radio galaxy ejected in a galactic explosion are strong sources of radiation at radio frequencies, these explosion generated groups are likely candidates for discovery in a search such as that conducted by Dr. Arp. We may logically conclude that at least some of those of Arp’s associations that have the required composition—a central galaxy that shows visible signs of internal disturbance, and two radio-emitting objects on opposite sides of this central galaxy, one of which is a quasar—are explosion systems. This provides us with an opportunity to make a clear-cut test of the validity of the theoretical conclusions.

If we were working with data of unquestionable reliability, we would simply go ahead with the calculations without further ado. But the task that Dr. Arp has performed is a difficult one, and it is unrealistic to expect that all of his “associations” define groups of objects of common origin. Indeed, the majority of his colleagues seem unwilling to concede any validity to these results, as would be concluded from the general preference for the cosmological explanation of the quasar redshifts, which attributes them entirely to the normal galactic recession. and thus denies the existence of the second redshift component that must exist if Arp’s associations are physically real. We are therefore in a position where we have a double task. We must verify the reality of the associations in the same operation by which we verify the theoretical redshift relation from the available data.

In order to deal with what may be a mixture of correct and incorrect identifications, it is necessary to rely upon probability considerations. If the quality of the data available for analysis is poor, it might not be possible to reach any definite conclusions by this method, as the results that we obtain may not differ enough from random probability to be statistically significant, but if a reasonable percentage of Arp’s identifications represent actual physical associations, some meaningful results can be obtained. Inasmuch as the theory being tested calls for the existence of a specific mathematical relation, any degree of conformity with that relation exceeding random probability is evidence in favor of the theoretical conclusion. A high degree of correlation, much in excess of random probability, is tantamount to proof, not only of the validity of the theoretical relation, but also of the accuracy of the identifications.

The nature of the process is such, however, that some stringent precautions are necessary in order to avoid introducing some kind of bias that would invalidate the probability argument. The most essential requirement is that the data that are utilized must be random with respect to the point at issue. One of the best ways to insure randomness is to utilize data that were previously compiled for some other purpose. Since Arp carried out his work for one purpose, and we are making use of it for an entirely different purpose, randomness of the data, with respect to the object of our inquiry, is achieved automatically.

One further requirement that must be observed, however, if conclusions based on probability considerations are to be beyond reproach, is that the data must be homogeneous, because unless they are homogeneous they are not likely to be completely random. We must therefore use only information that has been gathered on the basis of the same set of criteria and the same processes of judgment. This means that where a process of selection has been involved in accumulating the data, we must use these data in their original form, and exclude later additions or modifications, as it is practically impossible to maintain the original selection criteria unchanged over any substantial period of time. Even if a conscious effort is made to avoid changes events taking place in the interim, and the natural evolution of thinking in the course of time will alter the criteria in ways that are difficult to identify.

For this reason, the comparisons in this chapter are all based on Arp’s first extensive set of results, published in 1967, which was confined to objects included in the 3C (Third Cambridge) catalog of radio sources.²⁴⁴ Subsequent to this publication Dr. Arp modified some of his original groupings and identified a number of additional associations, some on the basis of the original considerations, and some on other grounds. But we cannot use this additional material in conjunction with the original, because if we do, we no longer have the homogeneous set of random data that is required in order to assure the validity of our probability arguments.

For example, Arp has found that there are several quasars located in a straight line apparently proceeding from the galaxy NGC 520, and he regards this as evidence of physical association. But an identification of association of quasars or other objects based on linear alignment is something quite different from an identification based on the presence of two radio emitters on opposite sides of a “peculiar” galaxy, and we are not justified in taking either of these into account when we are undertaking to apply probability principles to an assessment of the validity of identifications made on the other basis. Whatever conclusions we may draw from the NGC 520 alignment are separate and distinct from those derived from the study of objects from the 3C catalog selected on an entirely different basis. The additional material can, of course, be used for other studies of the same subject, and the results thereof are entitled to the same kind of consideration as the results of the present analysis, but it must be separate consideration.

With the benefit of the foregoing understanding as to what we propose to do, and how we propose to go about it, we may now proceed to an examination of the ten associations from Arp’s study of the 3C objects that are available for this purpose. His list is much longer, but for present purposes we are interested only in those associations in which one of the observed radio emitters is a quasar. On beginning the examination, the first thing that we encounter is the necessity of making some further exclusions, because the theory itself identifies some of the presumed associations as incorrect, and hence these associations cannot provide any comparison of theory with observation. Where the theory itself asserts that no agreement is to be expected, a demonstrated lack of agreement is meaningless.

Dr. Arp says that he does not expect to be able to identify the central “peculiar” galaxies beyond a recession of 10,000 km/sec.²⁴⁵ The quasar 3C 254, with a redshift of 0.734, of which 0.039 is the normal recession, is theoretically receding at slightly over this limiting recession speed, and is therefore approximately at the point beyond which the theoretically correct central galaxy is unobservable. According to the theory, then, any identification of a central galaxy with a quasar appreciably more distant than 3C 254 (in Arp’s association 148) is prima facie wrong, and a comparison of the redshifts has no significance. We can test the theory only by checking the correlation in those cases where the theory says that there should be an agreement. On this basis, the only significant correlations with the central galaxy are the first four in Table IV. In all of these cases the theoretical and observed values show a satisfactory agreement. (The ratio 2.78 for association 134 would not be satisfactory at a higher z value, but obviously the random motions and other incidental factors have a higher proportionate effect where the recession is so small).

Beyond the point where the correct galaxy of origin becomes unobservable it

TABLE IV

Association Number	Quasar Redshift	Basis of Calculation	Excess/z½
134	.158	C	2.78
160	.320	C	3.41
125	.595	C	3.31
148	.734	C	3.76
201	1.037	R	3.56
139	1.055	R	3.31
5055	1.659	R	5.59
Excluded
5223	.849	C	5.3
143	1.063	C	9.1
197	2.38	C	16.7

is still possible that the radio galaxy associated with a particular quasar may have been correctly identified, as the radio galaxies can be detected at distances well beyond those at which the features distinguishing a “peculiar” galaxy can be recognized. The correlations in our analysis have therefore been made on the basis of the radio galaxy, if the necessary redshift measurement is available, rather than the central galaxy, for all distances greater than that of association 148, as indicated by the symbol R in the third column of the table.

Here, again, there is an upper observational limit. It is somewhat indefinite, because of the wide range of emission energies. but the available evidence indicates that only the exceptional radio galaxy can be detected (or could be detected with the facilities available in 1967) at the distance corresponding to the theoretical location of the quasar 3C 280.1 in association 5055. The legitimacy of this association is therefore open to question. Since we must exclude associations 5223, 143, and 197 on the grounds previously cited, this questionable case, number 5055, is the only one in the entire list where there is a lack of agreement with the theory. All of the other associations in which the observed relation between quasar redshift and normal recession redshift could agree with the theoretical relation do show such an agreement.

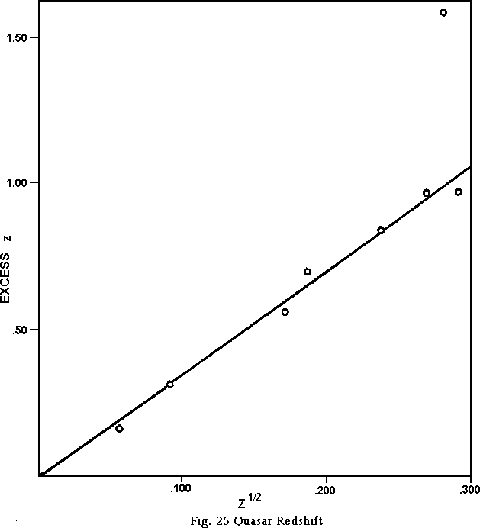
The relevant data from Table IV are shown graphically in Figure 25. Each plotted point on the graph indicates the relation of the excess redshift of the particular quasar, the amount by which the quasar redshift exceeds that of the galaxy with which it is presumably associated, to the square root of the redshift of the associated galaxy. The diagonal line shows the relation to which these points should theoretically conform. If the prevailing

astronomical opinion were correct, and the redshifts the quasars were due to the normal recession alone, there would be no definite relation between the quasar redshift and that of the object or objects that are grouped with it. In that event the plotted points would scatter randomly, not only over the area of the graph as shown, but also over a much larger area above it, extending up to a value of 30 or more, as can be seen from the figures applying to the “excluded” group in Table IV. The same would be true if the associations are real, but, as Arp himself suggests, the excess redshift is due to some cause other than motion, and hence not directly related to the normal recession.

But they are definitely not random. On the contrary, five of the six points fall essentially on the theoretical line; that is, within the margin that can be attributed to the distances the ejected objects have moved since the explosion, to random spatial motion, and other minor effects. The probability that five out of the six would by chance fall on a straight line coinciding with a theoretically derived relation is negligible. The results of the investigation are therefore conclusive. They constitute a positive verification of the theoretical 3.5 z^½ value of the explosion redshift.

All of the other evidence, both for and against the association of the quasars with objects of lower redshift, has been indefinite. Most of it rests upon correlations between the redshift of objects whose projections on the sky are close enough to indicate that these objects may be contiguous. As a general proposition a finding of this kind, a showing that some of the members of a given class conform to a specified relationship, has only a very limited significance. It remains little more than speculative unless further study enables defining a sub-class such that all of the members of this sub-class conform to the specified relation.

The reason why the results obtained by Arp are conclusive, whereas the other findings are not, is that Arp has done what no one else has been able to do; that is, he has defined a class of objects, associations of a specified nature between radio emitters included in the 3C catalog, which, when further limited by the criteria developed in this work, do conform to a definite and specific redshift relation. The associations that he has identified are not merely groups of objects whose observable positions indicate that they may be neighbors. They are groupings whose physical characteristics are similar, and are in agreement with the theoretical results of galactic explosions. Their identification depends not only on apparent proximity, but also on (1) abnormalities in the central galaxy (which are consistent with its having exploded), (2) radio emission from the presumed ejecta (which is characteristic of high speed explosion products), and (3) existence of the presumed ejecta in pairs at comparable distances and in positions on opposite sides of the central galaxy (the positions that they would occupy if they had been thrown off simultaneously in opposite directions as required by the theory). The number of associations included in Table IV is small, to be sure, but these are all of the associations of this type that Dr. Arp was able to identify among the objects of a catalog which, at the time of its compilation, covered all of the accessible extragalactic radio sources then known. In the sample area that it covers, the study is therefore comprehensive, and the results are conclusive.

These results show that the additional component that is present in the quasar redshift is due to a physical mechanism that is specifically refuted to the normal recession. The existence of two distinct components makes any hypothesis such as that of “tired light” untenable, while the fixed mathematical relation between the two components rules out anything, such as a redshift of gravitational origin, that is independent of the recession. Conventional physical theory has no other explanation to offer, but these features to> which the observations point are the same features that we find when we apply pure reasoning to the properties of space and time as defined in the postulates of the Reciprocal System of theory. The explosive event that is required by the theory produces exactly the kind of an association of three related objects—a central galaxy with a radio galaxy on one side and a quasar diametrically opposite—that Arp has identified in his studies. The ultra high speed imparted to the quasar by the tremendous amount of energy released in the galactic explosion exists in a second dimension of motion, and provides a second redshift component, related to but distinct from, the normal recession redshift, and the mathematical statement of that relation, as derived from theory is identical with the relation between the measured values.

While the pattern of redshift values illustrated in Figure 25 is conclusive in itself, it does not exhaust all of the corroboration of the theory that we can extract from Arp’s associations. The distances of the radio emitters from the central galaxy also have a significance in this respect. As explained in Chapter 15, gravitation is effective in all three scalar dimensions, and therefore operates against the explosion-generated motion as well as against the normal recession. As a result, the net explosion speed is initially small, and increases with the distance in the same manner, except for the two-dimensional effect, as the recession speed. On the other hand, since the greater part of the explosion speed is initially applied to overcoming the effect of gravitation, which operates within the fixed spatial reference system, there is a rapid change of position in the reference system during this initial period when the net total speed, including the scalar speed not capable of representation in this reference system, is quite small. The rate of change of position then decreases as gravitation is gradually overcome and the net speed increases. Thus the theory leads to the decidedly unconventional conclusion that the faster the quasar moves in the explosion dimension, the less its position in space changes.

According to the theory, the relative spatial speed of the quasar, the component that manifests itself by changing the quasar position in space, is the difference between I.0, the speed of light, and the explosion component of the quasar redshift, 3.5 z^½ in the quasars of Table IV. The relative speed of the radio galaxy is the average outward speed of the stars that fail to reach the 1.0 speed level, and are therefore ejected in space rather than becoming constituents of the quasar. Since the distribution of these speeds was initially the tail of a probability curve from l.0 downward, the average at the time of observation should be somewhat above 0.5, and nearly the same in all cases. Here, again, Arp’s associations provide a sample that we can test to see if this theoretical requirement is met. In these associations we can measure the ratio of the distances of the two ejected objects from the central galaxy, since the three objects lie on a straight line. Inasmuch as the distance traveled since the explosion is proportional to the average spatial speed, the distance ratio thus determined is also the ratio of the average speeds. Applying this ratio to the spatial speed in the explosion dimension derived from the redshift measurement, we arrive at the speed of the radio galaxy.

For this test we are able to use only those associations in which all three components central galaxies, quasars, and radio galaxies—have been clearly identified. Four of the associations listed in Table IV are within the 10,000 km/see range in which identification of the central galaxy is feasible, but the radio galaxy in association 148 is unidentified optically. Its approximate location is known, and it can therefore be included in the study, along with the three associations that are clearly identified, with the understanding that the results on 148 are subject to some uncertainty. Table V shows the observational data on these four associations, and the speeds of the radio galaxies as calculated from these data.

TABLE V

Association Number	Excess Redshift	Spatial Speed	Distance Ratio	R.G. Speed
134	0.155	0.845	0.73	0.62
160	0.312	0.688	0.91	0.62
125	0.566	0.434	1.35	0.59
148	0.695	0.305	2.57	0.78

Column 2 of the table gives the explosion redshift of the quasar in the association identified in Column 1. Column 3 is the relative spatial speed of the quasar, the difference between unity and the value in column 2. Column 4 is the measured distance ratio. Multiplying Column 4 by Column 3, we arrive at the speed of the radio galaxy, relative to an explosion speed of 1.0.

These results given in Column 5 meet the requirements set forth earlier, that is, they arrive at essentially the same speed for all four radio galaxies (if we make allowance for the lack of certainty in the position of the radio galaxy in association 148), and this calculated speed is within the limits that we can establish from more direct considerations. Furthermore, a very wide range of quasar speeds is included, as the theoretical spatial speed of the quasar 3C 273 m association 134 is twice that of 3C 345 in association 125, and almost three times that of 3C 254 in association 148. The downward trend in the relative distance of the quasars from the central galaxy as the speed increases is unmistakable.

Verification of a theoretical conclusion of this nature, one that is nothing short of outrageous in the context of conventional theory is particularly significant because it shows that a drastic change in fundamental theory is required before the full range of physical phenomena can be understood. The customary process of adjustment and modification of existing theory by means of additional ad hoc assumptions is clearly incapable of dealing with discrepancies of this magnitude. No amount of tinkering with the conventional theory of motion can reconcile a decrease in the rate of change of spatial position with an increase in speed. Some new light on the general situation is indispensable..

A related phenomenon that is equally inexplicable in terms of conventional physical thought is the nearly constant separation of the radio emitting regions in most quasars. Although the distances to different quasars vary over an extremely wide range, the apparent separation of the two radio components is usually close to a constant value. For example, Table VI shows the separations (in seconds of arc) measured by D. E. Hogg,²⁴⁶ excluding three values that will be considered later.

TABLE VI
COMPONENT SEPARATIONS

Quasar	Separation	Quasar	Separation
3C 181	6.0	3C 273	19.6
3C 204	31.4	3C 275.1	13.2
3C 205	15.8	3C 280.1	19.0
3C 207	6.7	3C 288.1	6.4
3C 208	10.5	3C 336	21.7
3C 249.1	18.8	3C 432	12.9
3C 261	10.8	MSH 13-011	7.8
3C 268.4	9.4

Similar measurements by Macdonald and Miley include a substantial proportion of larger separations, but these authors comment that their list includes many objects in which the radio components are so far distant from the optical center that, in their words, “If the radio structures of the larger QSOs were not symmetric about the optical QSO they might not have been identified.”²⁴⁷ This suggests that the quasars with the larger component separations represent a different group of objects, the members of which have a second observable set of laterally displaced components. Such a hypothesis is supported by a further comment from the investigators which indicates that, in some instances, both types of component separation are present in the same structures. “Many sources,” they say, “have large scale structure but small scale components dominate.”

The almost constant angular separation of such a large proportion of these radio components of quasars stands out as an observed fact for which conventional astronomical theory has no explanation. As expressed by K. I. Kellerman, “either: the linear dimensions of radio sources depend on redshift in just such a way as to cancel the geometrical effects of the redshift, or: The geometric effect of the redshift on apparent size is negligibly small.”²⁴⁸ Since neither of these alternatives can be accommodated within the boundaries of conventional theory. astronomy, Kellerman says, is confronted with a paradox.

In approaching the question theoretically. we note first that the outward radial movement of the quasars is beyond the limits of the reference system, and it is therefore incapable of representation in that system. As explained in connection with the derivation of the applicable general principles in Volume II, motion in a second dimension is normally excluded from representation in the spatial reference system because the presence of motion in the original dimension preempts the full capacity of the reference system. But when representation of the motion in the original scalar dimension is ruled out for some reason, representation of the motion in the second dimension becomes possible. The lateral motion of the distant quasars is analogous to the lateral magnetic motion discussed in Volume II. As in electromagnetism, the motion in the second dimension of the intermediate speed range appears in the reference system with a direction perpendicular to the line of motion in the original dimension. In the case of the quasars, this direction is perpendicular to the line of sight.

The recession speed in the second dimension is the same as in the dimension coincident with the reference system, but as observed it is reduced by the interregional ratio, 156.444. Since it originates in a two-dimensional region, it is observed as a second power quantity. Thus the ratio of lateral to radial motion is (2/156.444) . In the terms in which the astronomers generally express the lateral displacement, this observable recession in the lateral direction amounts to 16.9 seconds of arc.

Inasmuch as the outward motion of a quasar has a specific direction, as seen in the spatial reference system, the lateral motion is confined to one specific perpendicular line. As noted earlier, however, scalar motion does not distinguish between the direction AB and the direction BA. The lateral recession outward from point X is therefore divided equally between a direction XA and the opposite direction XB by the operation of probability. Matter moving translationally at upper range speeds thus appears in the reference system in two locations equidistant from the line of motion in the coincident dimension (the optical line of sight, in most cases), and separated by 33.8 seconds of arc.

It does not follow, however, that the separation observed from the earth will be this large. If the quasar is a distant one no evidence of its existence can be detected here until the radiation has had time to travel the long intervening distance. When first received. this radiation will disclose only the situation that existed at the location and time of ejection. before the lateral recession had begun The progress of the recession will be revealed gradually by the radiation subsequently received. but the observed recession will lag behind the true magnitude by the time required for the travel of the radiation, until the observed separation reaches the limiting value. In the meantime, the separation will be observed at some value intermediate between zero and the maximum.

l his explains why the observed separations vary, and arc generally less than the calculated 33.8 seconds of arc. As can be seen from the foregoing explanation these observed separations should be related to the time that has elapsed since the explosive event that produced the fast-moving products from which the radiation is being emitted. The relation of the optical and radio emissions provides a rough indication of this time. The ratio of these emissions is affected by the evolutionary changes that take place in the various stages of the existence of the quasar, but by limiting our consideration to a homogeneous group of objects we can minimize the effect of these changes. For such a group the radio emission should decrease with time, as the isotopic adjustment progresses toward completion, and the ratio of optical to radio emission should increase accordingly. The magnitude of this ratio should therefore give us an approximate measure of the relative quasar ages.

An appropriate group of this kind consists of the six quasars in Hogg’s list with redshifts above 1.00 for which luminosity data are available in the tabulations in Chapter 25. Examination of these data indicates that the approximate ratio (R_L) of optical to radio luminosity is related to the separation of the radio components (S) by the expression: S = 83R_L + 3.0. Separations calculated on this basis are compared with Hogg s measurements in Table VII.

TABLE VII
COMPONENT SEPARATIONS

Quasar	RL	Separation
		Calc.	Obs.
3C 204	0.279	26.2	31.4
3C 208	0.113	12.4	10.5
3C 432	0.112	12.3	12.9
3C 268.4	0.075	9.2	9.4
3C 181	0.033	5.7	6.6
3C 280.1	0.031	5.6	19.0

All but one of these correlations are within the range of variation that can be expected in view of the diversity of the conditions affecting the individual quasars. The reason for the discrepancy in the values applicable to the quasar 3C 280. l is not “known” but it could be the result of a second very recent, outburst that has renewed the radio emission. On this basis, the low R_L value is produced by the radiation from the second explosive event, whereas the 19.0 figure is the separation between the products of the earlier event.

The separations greater than about 35 seconds of arc that are included in the reports that were quoted, those of the three quasars omitted from the tabulation of the Hogg results, and a larger number from the work of Macdonald and Miley, arc due to a different cause. They are the results of actual motion of the ultra high speed dust and gas from which the radio emission originates, motion that has taken this material away from the location where the optical radiation is being produced. This is the process by which the separation of the radio components of the radio galaxies originates, and it will be examined in connection with the discussion of these objects in Chapter 26. As we will see there, this process is not operative beyond a distance of 1.00 in the explosion dimension (total redshift 1.081). Thus there should be no component separations above 33.8 seconds by more than the observational error at redshifts above 1.081. This is consistent with the findings of both of the investigations cited.

In addition to the major explosive events that produce the larger radio aggregates, there is also a continuing series of explosions of a more limited character (to be explained in Chapter 24) in the older quasars. In some instances these result in scattered centers of emission along the normal lateral line, but a large proportion of the total energy is generated by the radioactivity of the short-lived isotopes, which is observed at or near the optical location. As we will see shortly, there is also another factor that confines some of the radio emission in the older quasars to the center position. Thus there is a tendency toward three, rather than two, major locations of radio emission. The prevalence of the three-component pattern is illustrated in the data reported by Macdonald and Miley. These investigators say that only 6 of the 36 objects for which they determined radio structures are definitely double, whereas 23 have, or may have, a third component at the center. The remaining 7 are more complex.

The finding that the radio emission from the distant quasars originates mainly at the same spatial location as the optical emission, but that we see it at two or more locations in the reference system, is another conclusion that appears outrageous in the context of current physical thought, but like the equally unconventional findings previously discussed, it is in agreement with the physical observations, and provides the explanations for aspects of those Observations that are in conflict with conventional astronomical theory. In reality, it is not a strange or unusual phenomenon; it is merely unfamiliar. Multiple images produced by other means—mirrors, for instance—are commonplace.

All radiation from a quasar is subject to the same considerations, but the stellar constituents from which the optical emission originates are usually moving at speeds below the two-unit level. Thus the optical position of a quasar normally shows no lateral displacement. In some stars, however, the internal speeds may be in the ultra high range. In that event, both the optical and the radio emissions originate from the laterally displaced locations. The recently discovered cases of “twin quasars,” which are thought to be duplicate images produced by gravitational lenses, may well be single quasars with ultra high speed optically emitting components.

When the quasars have reached the point where their net speed exceeds two units and enters the cosmic range, the gravitational effect is inverted, and motion in time replaces motion in space. This eliminates the lateral recession in equivalent space that is responsible for the double character of the radio structure, as seen in the spatial reference system. The radiation from the quasar is still observable until the motion in time has continued long enough to destroy the status of the quasar as a spatial aggregate, and in the meantime this radiation is observed in the undisplaced radial location.

Observations indicate that many of the oldest of the visible quasars are in this transitional stage. A substantial proportion of those quasars that, on the basis of criteria such as the presence of absorption redshifts, large radio emission, and high z values, are in an advanced stage of development, show no spatial extension other than that corresponding to the spatial dimensions of the optical objects.

Thus the theory of the universe of motion provides an explanation of the major features of the quasar structures. Kellerman’s “paradox,” we find, is simply a message from nature, and it is the same message that we get from our analysis of the redshifts in Arp’s associations. It tells us that inasmuch as the lateral displacements, like the excess redshift, are directly related to the recession, and are therefore observable effects of motion, the conventional narrow view of motion, which limits it to speeds less than that of light and to effects that can be represented within a three-dimensional spatial system of reference, must be broadened. But this is not something new that we are just now finding out by examination of the astronomical situation. It is a direct consequence of the inherent nature of the motion of which the universe is composed, and it plays just as significant a part in the fundamental physical relations as in the astronomical phenomena we are now considering. The principles here being applied were developed deductively in the earlier volumes, and were there utilized in application to many physical phenomena. For example, the physical principle that explains why radio sources are double (or triple) is not peculiar to this particular application; it is a general property of scalar motion that has previously been shown to provide the explanation for such diverse phenomena as the induction of electric charges and the deflection of light by massive objects.

As demonstrated in this and the preceding chapter, the deductions from the Reciprocal System of theory, incorporating this more comprehensive view of the nature of motion, are in full agreement with the results of observation in the quasar areas examined thus far. In the pages that follow it will be shown that this one-to-one correspondence between the theoretical deductions and the observational results is maintained throughout the entire range of the quasar phenomena. Some of the features of the account of the origin and nature of the quasars thus derived are in conflict with current astronomical thought, to be sure, but this merely reveals the erroneous nature of much of the current thinking. For example, present-day theory sees no way in which the forces necessary to eject a galactic fragment can be built up within a galaxy. “Obviously d normal assemblage of stars cannot be hurled about like a snowball,” says Arp. However, the observational evidence makes it clear that fragments are ejected under some circumstances; that is, they are hurled about like snowballs. Current astronomical literature is full of references to, and hypotheses dependent upon, ejection of “assemblages of stars” from galaxies. In explaining how this is possible, and indeed, inevitable in the normal course of galactic evolution, the Reciprocal System is simply filling a conceptual vacuum.