CHAPTER 17
Pulsars
As indicated earlier, the maximum product speeds of the least powerful Type II supernovae, those in which the exploding star is relatively small, are in the intermediate range. Like the fast-moving products of the Type I explosions, the products of these smaller Type II supernovae are white dwarfs. On the average they are smaller than the white dwarf products of the Type I supernovae, and their iron content is less, but they follow the same evolutionary pattern. The ultra high-speed products of the more powerful Type II explosions follow a different course. As we saw in Chapter 15, they move linearly outward, and in the usual case ultimately arrive at a net explosion speed exceeding two units, and disappear into the cosmic sector.
Those of the ultra high-speed products that are expanding in time and moving linearly in space are fast-moving Stage I (not optically visible) white dwarfs. Their most distinctive feature is the intermittent nature of the radiation that is received from them, and for this reason they are called pulsars.
Up to the time when Quasars arid Pulsars was published in 1971, about 60 pulsars had been located. This number has now risen to over 300. Aside from the discovery of x-ray pulsars and the identification of their properties, progress in the pulsar field during the intervening years has consisted mainly of accumulating more data of the same nature as that available in 1971. There has been a great deal of theoretical activity, but since this has been based almost entirely on the “neutron star” hypothesis, no progress has been made toward recognition of what this work has identified as the true nature of the pulsars. This lack of basic progress is clearly demonstrated by the current inability to account for the two fundamental processes that are involved. As reported by F. G. Smith in a review of the existing situation, the manner in which the pulsar is produced by the supernova explosion “is not understood,” and “little is known about… the mechanism of the radiation.”183
Furthermore, no one can explain how the hypothetical neutron stars originate. As brought out in Chapter 6, the arguments advanced in support of the assumption of a “collapse” under the influence of self-gravitation are absurd, and no other way of producing “degenerate matter” has been identified. But the astronomers continue to insist that neutron stars must nevertheless exist.
Even now, however, we have no theories that satisfactorily explain just how a massive star collapses to become a neutron star. We know that neutron stars are possible in our universe only because we see that they are there—not because we understand how they form.184 (Martin Harwit)
Harwit defines a neutron star as “a collapsed, compact star whose core consists largely of neutrons.”185 Only one of the descriptive words in this definition is supported by the astronomical evidence. This evidence shows that the object that is being called a “neutron star” is indeed a compact object. But, as Harwit himself admits, there is no evidence to support the assertion that it is a “collapsed” star. No one can explain how a star could have collapsed. Nor is there any evidence that this object has a core, or that it is composed, to any significant extent, of neutrons. The definition does not define the observed object; it defines a purely hypothetical object dreamed up by the theorists.
Harwit says that “we see that they [the neutron stars] are there.” This is definitely not true. He and his colleagues see that compact stars are there, but the further assertion that these are neutron stars is pure assumption. It is simply another of the many instances where astronomical thought has lost touch with reality because of the prevailing tendency to assume that the most plausible theory available at the moment must necessarily be correct, regardless of how many questions it leaves unanswered, and how often it conflicts with the evidence from observation. The case in favor of the neutron star hypothesis is the same “there is no other way” argument that we have met so often in the earlier pages of this and the preceding volumes. Of course, the practice of arriving at conclusions by a process of elimination does have merit under appropriate circumstances. It is not the use, but the misuse, of this argument that is subject to criticism. As Fred Hoyle pointed out in connection with one of these misuses:
So the argument amounts to nothing more than the convenient supposition that something which has not been observed does not exist. It predicates that we know everything.186
This is the crux of the situation. The use of the “no other way” argument is legitimate only in those cases where we have good reason to believe that we do know everything that is relevant. In any case where the relevant factors are well understood, the elimination of all but one of the recognized possibilities creates a rather strong presumption (although still not a proof) that the one remaining possibility is correct, providing that this possibility does not involve any conflict with observation or measurement. The serious mistake that is so often made in present-day scientific practice, not only in astronomy, but in other areas of physical science as well, is in accepting this kind of an argument in cases, such as the assumption of the existence of neutron stars, where the foregoing requirements are not met. The result is that the distinction between fact and fancy is lost.
The distribution and observed properties of the pulsars indicate that they are situated within, or close to, the Galaxy. Since one of them is associated with the Crab Nebula, and another with the Vela Nebula, both supernova remnants, it seems evident that the pulsars are products of supernovae. The validity of this currently accepted conclusion is confirmed by our theoretical development. The fact that both of these objects are located in Type II remnants also supports our finding that the pulsars are products of Type II explosions only. Some members of the astronomical community are reluctant to accept this conclusion, as it is difficult to reconcile with current views as to the nature of the pulsars. Shklovsky, for example, admits that “The two known pulsars in SNR are associated with SN II explosions,”187 but nevertheless expresses the belief that pulsars may yet be discovered in association with Type I remnants. The conclusion that no pulsars form in Type I explosions is “at least premature,” he contends. His argument is that the light curves of all supernovae are best explained by continued input of energy from pulsars within the remnants, in the manner assumed in the case of the Crab Nebula, and that the pulsars therefore probably exist in Type I remnants even though none have been detected.
The truth is that Shklovsky’s argument is very much stronger if it is turned upside down. It contains three statements: (1) the energy in the Crab Nebula is supplied by the pulsar (neutron star in current thought), (2) the power supply is the same in all remnants, and (3) the observations show that there are no pulsars in Type I remnants. Shklovsky assumes that statement (1) is valid, and deduces from the foregoing that statement (3) is false. But (3), the observation, is far more reliable as a premise on which to base our reasoning. If we take this observation at its face value, we deduce that statement (1) is false, and that the energy of the Crab Nebula is not supplied by the pulsar. This agrees with the conclusion that we reach by deduction from the postulates of the theory of the universe of motion.
Those astronomers who reject the idea that there are concealed pulsars in Type I remnants have no explanation for the restriction of the pulsars to Type II events, but generally agree with F. G. Smith that “the association with Type II supernovae seems established without further argument.”188
No pulsars have been discovered in external galaxies, but as noted in Chapter 15, there are a few remnants of Type II supernovae in the Large Magellanic Cloud, indicating that pulsars occasionally do appear in relatively small galaxies, as well as in the larger aggregates. This is consistent with what we have previously found with respect to the existence of a few older stars in the younger galaxies.
In a number of instances, the observations of the pulsars arrive at results that seem contradictory. It has been found that many, probably most, of them are moving rapidly, with speeds often exceeding 100 km/sec.189 Furthermore, the average height of the pulsars above the galactic plane is considerably greater than is normal for the objects from which they presumably originated. These motions and positions are seemingly inconsistent with the fact that the Crab and Vela pulsars have remained near the center of their respective remnants.
In the universe of motion, the spatial position of the pulsar and its observable spatial speed are related to the gravitational retardation. The explosion speed, and the resulting change of position in a second scalar dimension of space, are not capable of representation in the spatial coordinate system, but, as we saw in Chapter 15, when a portion of the gravitational motion is eliminated by the oppositely directed motion generated by the explosion, the outward motion that was being counterbalanced by gravitation becomes effective, and appears as an observable spatial motion equal in magnitude and opposite in direction to the gravitational motion that is neutralized. Thus, during the first portion of the outward travel of the ultra high speed explosion product, there is an observable spatial speed, and a corresponding change of position in the reference system, the magnitude of which depends on the strength of the gravitational force that has to be overcome.
The gravitational effect on an object moving through a portion of the Galaxy is continually changing. Initially the exploding star is outside the gravitational limit of its nearest neighbor (unless it is a member of a double or multiple system), and the gravitational restraint on the pulsar is mainly due to the mass of the slow-moving remnants of the explosion. This effect decreases rapidly, and as the pulsar moves farther away from the initial location, the integrated effect of all mass concentrations within effective range becomes the dominant factor.
This variation in the gravitational restraint explains some of the observations that otherwise seem mutually contradictory. All pulsars are moving. If the supernova explosion occurs in an isolated star in the outer regions of the galaxy, the gravitational restraint on the pulsar is relatively weak, and the outward movement resulting from elimination of the gravitational effect is correspondingly small. The Crab pulsar, for example, is moving very slowly with respect to the nebula, and according to present estimates it will not escape for about 100,000 years.199 At present it is still near the center of the nebula.
On the other hand, pulsars produced by explosions that are more centrally located in the galaxy are subject to substantial gravitational forces due to the effects of the central mass as a whole. In this case, the spatial component of the explosion speed, which causes a change of position in the space of the reference system, is relatively large. It follows that, as a rule, we can expect to find the pulsars produced by isolated stars in the outer regions of the galaxy moving quite slowly and located in or near the remnants, whereas those produced in central locations will be moving rapidly, and most of them will be found well away from the galactic plane. The pulsars produced in binary or multiple star systems, or in clusters, are subject to more gravitational restraint than the single stars, and if they are located in the outer regions they follow an intermediate course, not attaining the high speeds of those produced in the central regions, but moving fast enough to leave the vicinity of the remnants within a few thousand years. This accounts for the absence of pulsars from most of the observable remnants.
Another apparent anomaly is that the observed number of pulsars in the Galaxy seems to require a rate of formation that is considerably in excess of the observed frequency of Type II supernovae. Smith calls this “a serious discrepancy between the theory of origin of pulsars in supernovae, and the observations of their ages and numbers in the Galaxy.”191
Our findings clarify this situation. On the basis of theoretical conclusions reached in the preceding discussion, the number of Type II supernova explosions occurring in the Galaxy is not only ample, but greatly in excess of that required to account for the observed number of pulsars. However, our findings are that the oldest stars, the ones that reach the age limit and explode as supernovae, are concentrated mainly in the central regions of the galaxy, the oldest portions of the structure. The great majority of the Type II supernovae therefore take place in these central regions, where they are unobservable because of the strong background radiation and obscuration by intervening material. Furthermore, since the stellar aggregates have the general characteristics of viscous liquids, they resist penetration by the explosion products. In the central regions of the largest galaxies, the overlying matter confines all of the explosion products, and the pulsars included in these products are, like the supernovae, unobservable individually. In galaxies of less than maximum size, such as the Milky Way, some of the pulsars originating in the outer portions of the central regions are able to make their way out to join the pulsars originating from isolated supernovae in the galactic disk. Thus there is no difficulty in accounting for the number of Type II supernovae required in order to support the estimated pulsar population.
Conventional pulsar theory rests to a large extent on the current interpretation of the observations of the Crab Nebula. According to these ideas, the emission of radiation from the nebula is powered by energy from the pulsar located at its center. But only a few of the known pulsars are associated with supernova remnants (only two such associations are definitely confirmed). Some other explanation of the long-continued emission of energy from the other remnants is therefore required in any event, and when this is available there is no need for a special process in the Crab Nebula. The theory of the universe of motion supplies a source of energy that is independent of the existence of pulsars in the remnants.
The most characteristic property of the pulsars, the one that has given them their name, is the pulsating nature of the radiation that we receive from them. In the early days of the pulsar investigation, just after the discovery of the first of these objects, the extreme regularity of the pulses and the absence of any known natural process whereby they could be generated, suggested that the pulses might be artificially produced, and for a time they were facetiously called messages from little green men. When more pulsars were discovered it became evident that they are natural phenomena, and the little green men had to be abandoned, but no explanation of the origin of the pulsed radiation that the astronomers have been able to put together thus far is any less fanciful than the little green men. As F. G. Smith, one of the prominent investigators in the field, said in the statement previously quoted, “little is known” in this area.
The big problem is that natural processes capable of producing regularly pulsed radiation are hard to find within the arbitrarily circumscribed boundaries of conventional physical science. The only such process thus far suggested that has received any appreciable degree of support is rotation. In the absence of any competition, this is the currently accepted hypothesis, although, as indicated in the statement by Smith, it is recognized that this explanation has not been developed to the point where it can be considered satisfactory. It depends too much on the assumed existence of special conditions of which there is no observational evidence, and it leaves a number of the observed properties of the pulsars unaccounted for. Furthermore, when the rotation process is applied to explaining the periodicity, the theorists are precluded from using it to explain some other phenomena that, on the basis of the observational evidence, and independently of any theory, are almost certainly due to rotation—the “drifting sub-pulses,” for example.
In the universe of motion, the periodicity of the radiation received from the pulsars is a necessary consequence of the property that makes them pulsars: the ultra high speed. An object moving in the explosion dimension with a speed in this ultra high range arrives at the gravitational limit when its net speed in this dimension (the explosion speed minus the effective gravitational speed) reaches unity. At this point the effective gravitational speed, as we saw in Chapter 14, is equal to the oppositely directed unit speed of the progression of the natural reference system. On the basis of the theory of radiation set forth in the earlier volumes, this means that at the gravitational limit radiation is being emitted at such a rate that we receive one unit of radiation from each mass unit per unit of area per unit of time. At distances beyond this limit, the average amount of radiation received is less because of the further distribution over equivalent space. But radiation is a type of motion, and motion exists only in units. The decrease in the average amount of radiation received can therefore be accomplished only by a reduction in the number of units of time during which radiation is being received. Radiation from a pulsar beyond the gravitational limit is received at the same strength as that from one at the gravitational limit, but only during a constantly decreasing proportion of the total time. All of the mass units of a star enter the pulsation zone within a very short time, only a small fraction of the observed period. Thus, even though the total radiation from the star is distributed over an appreciable time interval, it is received as a succession of separate pulses.
All pulsar periods are lengthening (except in the pulsating x-ray emitters, which we will consider in Chapter 19). The period is thus clearly an indication of the age of the pulsar, but the specific nature of the relation is not immediately apparent. At first it was believed that the age could be determined by simply dividing the period by the rate of change, and “characteristic ages” thus defined are found in reference works. But it is now evident that the situation is more complicated, and that most of the ages thus calculated are too high.
The first study of the pulsar ages in the context of the Reciprocal System of theory likewise took a wrong turn, and arrived at ages that are now seen to be too low. As pointed out in Volume I, the status of this system of theory, the theory of the universe of motion, as a general physical theory means that it should be able to provide the correct explanation for any physical situation. But this explanation does not emerge automatically. A substantial amount of study and investigation may be required in any specific case before the correct answers are obtained. The first such study frequently turns out to be deficient m some respect. Relevant factors may have been overlooked, or may not have been taken fully into account, even where the development of theory may have been correct, so far as it went. This was the case in the original pulsar study, which we now find arrived at results that are correct in their general aspects, but require modification in some of the details. A full-scale review of the pulsar phenomena undertaken in connection with the preparation of the text of this new edition has clarified a number of points that were not correctly interpreted either in conventional astronomical thought or in Quasars and Pulsars. This clarification is still not complete, but some significant advances in understanding have been accomplished.
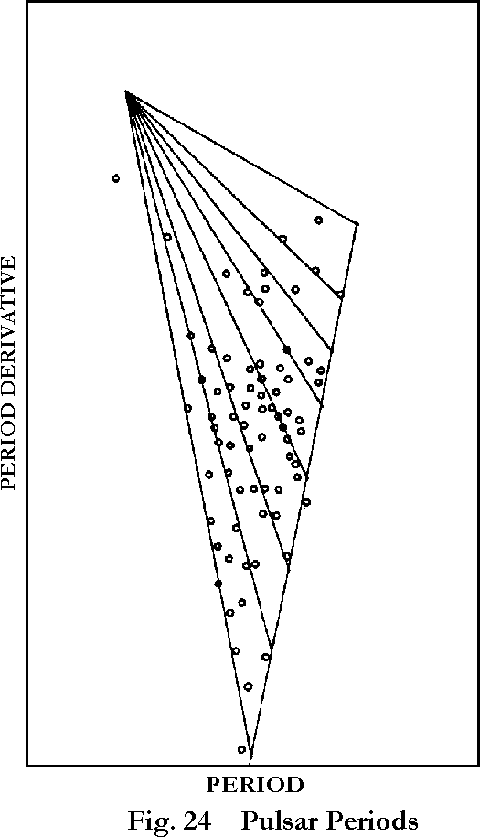
Figure 24 is a diagram that is found in many recent discussions of the pulsar period relationship, with some lines added for purposes of the present review. It is recognized that the diagonal line at the right of the diagram, with a slope proportional to the fifth power of the period, represents the cut-off at which the pulsed radiation ceases. It is also realized that there must be some significance in the absence of observations that fall in the lower left part of the diagram. But, in essence, what this diagram does for the astronomers is to identify some of the questions. It does not give the answers.
In the context of the theory of the universe of motion, the outer boundary of the material sector, the sector of motion in space, is a spatial limit. Since space and time, in this sector, are subject to the relation s = at2, where a is a constant applicable to the specific phenomenon involved, the time magnitude
that enters into the quantities related to the sector limit is t2 Furthermore, the sector limit applies to the total motion, the motion in all three scalar dimensions; that is, to t6. The time interval between successive radiation pulses, the period of the pulsar, is related to the total time. The rate of change of the period, as observed, is therefore the derivative of P. The period decreases with time, but because of the inversion at the unit level, the applicable quantity is not the derivative of the reciprocal of P6; but the reciprocal of the derivative of phi that is, the reciprocal of 6 P5.
This indicates that the points farthest to the left in Figure 24 define another and with the same slope as the cut-off line on the right of the diagram, and intersecting the latter at a period of about 0.62, as shown in the diagram. This downward-sloping line is the path of the period-derivative relation for a pulsar that conforms to the 1/6 P 5 relation without modification, and 0.62 seconds is the period at which the pulsar reaches the sector limit. As we saw in Chapter 15, however, the are eight ways in which the motion in the region of equivalent space can be distributed, only one of which results in transmission of the effects across the boundary into the three-dimensional region. Where the motion is distributed over n of the eight, the observed period is increased to nP Or. if we let P represent the observed period, the true period becomes P/n, and the reciprocal of the derivative is 1/6 (n/P)5. Each distribution thus has its separate path extending from the same initial point to a terminus on the cut-off line at a period of 0.62 n seconds.
While the observed points clearly follow the theoretical lines, as shown in Figure 24, in some instances, there is also considerable scatter in the diagram, the significance of which is not yet clear. The existence of half-integral effective values of n is undoubtedly one of the contributing factors. As we have noted frequently in the pages of the earlier volumes, in cases where the probability considerations favoring n and n + 1 are nearly equal, the result often is that half of the units involved take the n value and the other half the n + 1 value, making the effective magnitude n + ½ The existence of an evolutionary line based on n = 1½ is SO evident that this line has been included in the diagram. Similar half-integral values may exist throughout the total range, and this may be all that is needed to explain the scatter of the observed points. If not, there probably are some transitions from one value of n to the next as the net speed increases.
At the present stage of the theoretical development it is not possible to arrive at a firm theoretical value for the reference magnitude, the period corresponding to the sector limit where n = 1. In fact, this period may be, to some extent, variable. The value 0.62 seconds quoted in the foregoing discussion has been derived empirically by fitting the theoretical shape of the diagram in Figure 24 to the observed points.
The pulsar age involves another reference value for which we will have to use an empirically determined magnitude, 3.25×105 years, pending further theoretical study. The current age of the pulsar is the product of this value, the distribution factor n, and the square of the period in terms of the 0.62 unit (that is, (P/0.622 For the Crab pulsar, which is designated 0531 + 21, from which the value of the age constant was derived, we have (0.033/0.622 × l × 3.25×105 = 921 years. The Vela pulsar, 0835-45, is on the 1.5 evolutionary line, and its theoretical age is (0.089/0.062)2 × l.5 × 3.25×105 = 10046 years. This agrees with the age of the supernova remnant, estimated at about 10,000 years. The theoretical life spans of these two pulsars, if they stay on their present evolutionary paths, are 3.25×105 years and 1.10×106 years respectively. The maximum concentration of pulsars is on, or near, the lines with n values of 2 and 3. The corresponding lifetimes are 2.6×106 and 8.8×106 years. These results are consistent with current estimates based on observation of various pulsar characteristics. F. G. Smith, for instance, arrives at this conclusion: “We therefore take… the maximum lifetime for most pulsars as 3×106 years.”192
From the theoretical explanation of the nature of the pulsation it is evident that the shape, or profile, of the pulse is a reflection of the shape of the radio structure of the object from which the radiation is emitted. The dimensions of the pulsar in the line of sight, determine the width and amplitude of the pulse. Thus the pulse profile is a representation of a cross-section of the pulsar or, more accurately, the summation of a series of cross-sections.
The most common profile, a single hump, with or without irregularities, clearly originates from a globular object, which may be somewhat irregular. This simple profile, called Type S. predominates in the younger pulsars, those in the upper left of Figure 24. As explained in Chapter 15, however, an object whose components are moving at speeds in the ultra high range, between two and three natural units, appears to observation at radio frequencies as a double structure. The separation, initially zero. increases with the distance, and most of the older pulsars therefore have complex profiles, Type C, with double or multiple peaks.
As the rotation of the pulsar carries its various features across the line of sight, the amplitude of the radiation varies, giving rise to variations in the individual pulses. But when the data on these individual pulses are combined into an integrated profile that reflects the total emission during the full rotational cycle, the profile remains constant, except to the extent that actual changes in the pulsars (movement of local concentrations of matter, etc.) take place. The integrated profiles therefore show “well-organized and characteristic behavior.”193
The rotation imparted to the pulsar by the original explosion is generally quite limited, and ordinarily it takes from 500 to 2000 or more pulses for the integrated pulse profile of a young pulsar to reach the stable form which indicates that a full rotational cycle has elapsed. Interaction with the environment tends to increase the rotational speed, and many of the older pulsars, those approaching the cut-off line in Figure 24, are rotating fast enough to cause an observable drift of the sub-pulses. “The sub-pulses of successive pulses tend to occur at earlier phases, so that they drift fairly uniformly across the profile.”194
It has been noted by observers (see, for instance, Manchester and Taylor, reference195) that differences between the pulse shapes at radio and optical frequencies, together with the discontinuity between the corresponding spectra, suggest different emission processes, whereas the time coincidence of the peaks indicates that the processes are closely related. These seemingly contradictory observations are explained by our finding that the time pattern of the pulses of radiation is independent of the process by which the radiation is produced. At any specific time, all of the radiation emitted from the matter in a specific section of the pulsar becomes observable, irrespective of its origin.
Inasmuch as the pulsation is due to the attenuation of the radiation by distance, rather than to any feature of the emitter or the emission process, radiation from all objects moving at ultra high speeds is received in pulsed form if emitted during the time that the object is passing through the pulsation zone, irrespective of the nature of the emitting object. However, the radiation from the giant clouds of particles that constitute the second type of ultra high speed explosion product is too diffuse to be observed, while that from galaxies or galactic fragments is unobservable because the individual stars of which these aggregates are composed are so far apart that the pulsations in the radiation received from them are not synchronized.
Since the pulsar radiation originates in a two-dimensional region, it is distributed two-dimensionally; that is, it is polarized.
Individual pulses, and especially those that have a simple Gaussian shape, are highly polarized… The polarization often reaches 100 percent.196 (F. G. Smith)
According to the theory of the universe of motion, all radiation originating in the intermediate speed range is 100 percent polarized at the point of origin, but there are many depolarizing influences along the line of travel in most cases. The observed percentage of polarization is an indication of the amount of depolarization rather than of the initial situation. Thus we note that the radiation from the short-period pulsars with simple pulse profiles, classified as Type S. which have not yet had time to separate from the cloud of debris at the site of the supernova explosion, is weakly polarized, while that from the long-period complex (Type C) pulsars shows strong polarization.197 Similarly, the sub-pulses and micropulses are, in general, more highly polarized that the integrated profiles, a difference that is generally attributed to depolarization.198
Development of the details of the universe of motion as they apply to the pulsar phenomena has not yet been carried far enough to arrive at firm conclusions concerning the quantitative relations. We can, however, obtain some tentative results that are probably at least approximately correct. According to the findings described in the preceding pages, the size of the pulsar is indicated by the width of the pulse. The basic period, we found empirically, is 0.62 seconds. The equivalent space is 0.62 × 3×105 km = 1.86×105 km. The average width of the pulse is reported to be about three percent of the period.199 The indicated diameter of the average pulsar is then 0.03 × 1.86×103 km = 5580 km. On this basis, most pulsars are in the range from 5000 to 6000 km in diameter. This is within the white dwarf range.
We may now divide the corresponding circumferential distance by the time required to stabilize the integrated pulse profile, and arrive at an approximate value of the equatorial speed of rotation. For a rapidly rotating pulsar that reaches a stable pulse form in 10 pulses of one second each, the equatorial speed is about 1800 km/sec. This is very fast, but not out of line for an object that has been traveling at an extremely high speed. It is an order of magnitude less than some of the rotational speeds suggested in connection with previous theories.200 Where 1000 pulses are required before the integrated profile is stable, the equatorial speed is less than 20 km/sec.
One of the major advantages of a general physical theory is that it is a theory of the unknown physical phenomena of the universe, as well as a theory of the known phenomena. Of course, as long as a phenomenon remains unknown it is not particularly helpful to have a theory that explains it, unless that theory helps, in some way, to make discovery of the phenomenon possible. But once the hitherto unknown phenomenon is discovered, the existence of a general theory leads almost immediately to an understanding of the place of this phenomenon in the physical picture, something that may take a long time to achieve if no theory is available in advance.
In the case of the pulsars, the development of the astronomical aspects of the theory of the universe of motion had already been carried far enough prior to their discovery to provide an explanation of the nature and properties of the general class of objects to which they belong: ultra high speed products of stellar disintegration at the age limit. The deductions made in the course of the original investigation, and published in 1959, will be discussed in Chapter 20. This early investigation was directed primarily at the products of galactic explosions, but as soon as the pulsars were discovered, it was evident that these objects belong in the same class as the galactic explosion products whose existence was predicted in the 1959 publication, differing only in those respects where size is a significant factor.
Conventional science, on the other hand, has no general physical or astronomical theory, and this has left the pulsar field wide open for speculation. The theorists’ imaginations have had full play. As matters now stand, the prevailing opinion is that the pulsars belong to the hypothetical category of “neutron stars.” Where difficulty is experienced in fitting the neutron stars into the picture, a further exercise of the imagination produces a “black hole.”
In considering the conflicts between current astronomical thought and the theory of pulsars derived from the postulates of the Reciprocal System, it should be recognized that there is no independent evidence of the existence of such things as neutron stars or black holes. They are purely hypothetical, and they have been introduced only because accepted ideas as to the nature and properties of the white dwarfs impose limits on the roles that these objects can play in physical phenomena; limits that are wholly theoretical and have no factual support. From an observational standpoint, all of the high-density stars are alike. There is no physical evidence to indicate any division by sizes of the nature required by present-day theory. The truth is that the inability of the conventional white dwarf theory to account for the full range of these observationally similar objects is a serious defect in the theory; one which, in most fields of science, would be enough to prevent its acceptance. But in this case, the weakness in the white dwarf theory is used as an argument in favor of the black hole theory, or at least, as conceded by some of the proponents of the theory, it is a “key link” in that argument.201
When the existence of matter at extremely high densities was first brought to light by the discovery of the white dwarf stars it was found possible to devise a theory of this density that appeared plausible in the context of the facts that were known at that time. But later, when the same phenomenon—extremely high density—was encountered in the quasars, where the white dwarf theory that had been constructed is obviously inapplicable, instead of taking the hint and reexamining the white dwarf situation, the theorists directed their efforts (so far unsuccessfully) to finding some different explanation that would fit the quasars.
Then, when the same extremely high density showed up in the pulsars, still another explanation was required, and this time the neutron star hypothesis was invented. Further discoveries have revealed the existence of extremely high density in material aggregates of other kinds where neither white dwarf theory nor neutron star theory meets the requirements. So here we must have another new theory, and the resourceful theorists have brought forth the black hole. Thus, in order to explain the different astronomical manifestations of one physical phenomenon—extremely high density of certain material aggregates—we have an ever-growing multitude of separate theories, one for the white dwarfs, one for the pulsars, at least two for the x-ray emitters, several for the dense cores of certain types of galaxies, and no one knows how many for the quasars.
Even in astronomical circles, the absurdity of this situation is beginning to be recognized. For instance, M. Ruderman made this comment recently:
Theoreticians have apparently found it easy to understand them [the pulsars] for they have produced not only a theory of pulsars but dozens of theories of pulsars.202
The application of the Reciprocal System of theory to this problem merely accomplishes something that was long overdue in any event: a reevaluation and reconstruction of the entire theory of extremely dense aggregates in the light of the increased amount of information that is now available. This theoretical development shows that the extremely high density results, in all cases, from the same cause: component speeds exceeding the speed of light, unit speed in the universe of motion. All of the stars with extremely high density, regardless of whether we observe them as white dwarfs, novae, pulsars, x-ray emitters, or unidentified sources of radio emission, are identically the same kind of objects, differing only in their speeds and in the current stage of their radioactivity. Quasars are objects of the same nature, in which the extremely fast-moving components are stars rather than atoms and particles.