CHAPTER 11
Planetary Nebulae
Inasmuch as the system of reference by means of which we define the positions of physical objects in the material sector of the universe, the sector in which we are located, is stationary in space, but moving at the speed of light in time, we cannot detect objects moving in time, except during an extremely short interval while they pass through our reference system, and then only atom by atom. As explained earlier, however, if the net total three-dimensional scalar speed is below the point of equal division between motion in space and motion in time, any time motion component included in the total acts as a modifier of the spatial motion—that is, as a motion in equivalent space—rather than as an independent motion in actual time.
The nature of the modification depends on the magnitude and dimensions of the motion being modified. The participation of time motion in combinations of motion that are multi-dimensional in space (ultra high speeds) will be discussed later, in another connection. The motion with which we are now concerned, motion at intermediate speeds, is one-dimensional, but the original unit of speed (motion in space) has been extended linearly to a second unit, which is a unit of motion in time. Because of the effect of this time component, the successive spatial positions of an object moving freely at an intermediate speed do not lie on a straight line in the reference system as they would if the speed were less than unity. Motion in time has no direction in space. The spatial direction of each successive unit of the time component of the intermediate speed is therefore determined by chance. However, the average position of the freely moving object follows the straight line of the purely spatial motion, because the total three-dimensional motion is still on the spatial side of the sector boundary.
As a result of this time effect, the radiation from a white dwarf in its early stages is not received from the surface of the star itself, but from a much larger area centered on the average stellar location. When the inherently weak radiation from this (spatially) very small star is further diluted by being spread out over this wide area it is reduced below the observable level. It follows that the white dwarfs expanding back toward the material sector (evolutionary stage 2) are not observable at all as long as their surface temperature is above the level corresponding to the unit speed boundary. On that boundary the change of position in time (equivalent space), relative to the natural datum, the unit speed level, is zero, and the radiation from the white dwarf is received at full strength. The white dwarf stars therefore become observable at this point.
Our first concern will be with the relatively large stars, those whose mass exceeds a certain critical level that we will identify later. The detailed study of the white dwarf stars and related phenomena in the context of the theory of the universe of motion is still in the early stages, and we are not yet in a position to calculate the entry temperature for this class of white dwarf, but it can be evaluated empirically, and is found to be in the neighborhood of 100,000 K.
At this temperature, where the relatively large white dwarf enters its third evolutionary stage, it is still a gas and dust cloud in equivalent space; that is, it is in the gaseous state. In this gaseous state in time the B-V color index for a given temperature is different from that of the stars on the spatial main sequence. We find empirically that the color index corresponding to the 100,000 K temperature of the incoming white dwarfs is about -0.3. On the main sequence this index corresponds to a temperature of about 30,000 K.
Theoretically, these temperatures should be related by a factor of three. On entry into the observable region, the white dwarf is moving in all three dimensions of time (equivalent space). The radiation from this star, the wavelength of which determines the color, is one-dimensional. From the color standpoint, therefore, the radiation consists of three independent components, each of which has the wavelength and color corresponding to one third of the total rate of emission of thermal energy. The temperature, on the other hand, is determined by the total energy emission. Thus the color index of the newly arrived white dwarf of the class we are now considering is the same as that of a spatial main sequence star with a temperature one third that of the white dwarf. Since we do not have the theoretically correct values at this time, we will continue using 100,000 K and 30,000 K, with the understanding that these values refer to a temperature of about 100,000 K and a temperature one third as large, approximately 30,000K.
The location of the -0.3 index on the CM diagram coincides, in general, with the position of a rather obscure class of stars known as the hot subdwarfs. The “evolutionary status” of these stars “has not been really understood.”125 say Kudritzke and Simon, but current opinion apparently favors the suggestion that “On the way to becoming a white dwarf, while it is still very hot and just before the thermonuclear reactions cease, a star may find temporary stability in the region below the main sequence.”102 In short, this is presumed to be a way station on the totally unexplained, and poorly defined, route by which, according to current theory, a red giant becomes a white dwarf.
Observational information about these hot subdwarfs is still scarce and somewhat uncertain. A 1961 report by K. Hunger, et al.. says that “little is known about their precise location in the H-R diagram.”126 These authors make the following comments on matters that are relevant to the present discussion: (1) a major fraction of these stars are binaries, (2) some of them are central stars of planetary nebulae, and (3) the mass of one of them, the star HD 49798, has been evaluated as 1.5 solar masses. According to our findings, all of these stars are binaries. The relevance of the other two items will appear as our examination of these stars proceeds.
During the interval between the supernova explosion that produced the white dwarf and the reentry of that star into the reference system, where it is subject to observation, the portion of the original material ejected into space at less-than-unit speeds has also undergone some changes. Immediately following the explosion, the density of the material moving outward was sufficient to carry everything in the vicinity along with it, and the visible object was a rapidly expanding cloud of matter. As the expansion proceeded, the density of the cloud decreased, and in time a point was reached where the outgoing matter passed through the interstellar material rather than carrying that material with it. Eventually the outward motion of the ejected matter came to a halt, and inward motion began under the influence of gravitation, as explained in Chapter 4.
The existence of the hot subdwarfs suggests that the turnaround time is less for the material dispersed in time than for the material dispersed in space, and that the hot star is visible for a time before there is any substantial inflow of material from the environment. But eventually the matter that is being pulled back by the gravitational forces begins falling into the star. The first material of this kind reaching one of these newly arrived white dwarf stars. the hot subdwarfs, encounters the extremely high temperature of this object, and is heated to such an extent that it is ejected back into the surroundings. Since both the incoming and the outgoing material are at a very low density. there is only a limited amount of interaction, and the cold material continues to flow inward through the outward moving matter.
When the incoming matter reaches the hot surface of the star it is not only heated to a very high temperature, but is also strongly ionized. The outgoing ionized matter emits visible radiation, and we therefore see a sphere of ionized matter centered on the young white dwarf. The radiation from ionized atoms occurs when they drop to a lower state of ionization, and as a consequence the greater part of it takes place after the ejected material has traveled far enough to lose a substantial part of its original ionization energy, and before that energy is all dissipated. This leaves a nearly invisible region in the interior of the sphere. To the observer, the resulting structure has the appearance of a ring. Such an object is a planetary nebula.
Here we see the significance of the observation, cited above, that some of the hot subdwarfs are central stars of planetary nebulae. According to our deductions from theory all of the hot subdwarfs will become central stars of planetary nebulae in due course.
The planetaries are all far distant from our location, and it is difficult to get an accurate observational picture of the complicated processes that are under way in them. Consequently, there is considerable difference of opinion as to just what is happening.
Although we seem to comprehend the broad outlines of their formation and development, much of what we see is confusing and not at all well understood.127 (James B. Kaler)
The outward motion of the ionized gas in the typical large nebula is well established, and the general tendency is to take this as indicating that the central star, which is conceded to be a white dwarf, or on the way to becoming a white dwarf, is ejecting mass into its surroundings as a part of the process which, according to current ideas, will eventually reduce it to a burned-out cinder. This observed outward flow of matter seems, on first consideration, to define the nebula as an expanding cloud of material. But there are strong indications that this simple view is incorrect. One significant point is that the nebulae are not actually expanding at the rates indicated by the measured speeds of the outgoing matter. Indeed, some of the nebulae are not expanding at all. For instance, velocity measurements indicate that the diameter of NGC 2392, the Eskimo Nebula, is increasing at the rate of about 68 miles per second. But no definite increase in size is shown in photographs taken 60 years apart.
Our findings now indicate that the prevailing view of the nebulae as expanding structures is incorrect. Instead of being a rapidly dissipating cloud of material ejected from the central star in a single burst, or succession of closely spaced bursts, our analysis indicates that the planetary nebula is a relatively permanent ionization sphere through which the outgoing stream of material flows. We might compare it to the visible area of a river illuminated by the beam of a searchlight.
A report by M. and W. Liller concedes that “Very possibly, all planetary nebulae are ionization spheres,”129 but contends that in general these ionization spheres are expanding, although at a slower rate than would be indicated by the measured velocities. The size of the ionization sphere depends on the temperature of the central star and on the density of the nebula, increasing with higher central temperature and decreasing with higher density. The temperatures of the central stars necessarily decrease from the 100,000 K initial level. There is little or no loss of matter from the planetary nebula system, since the initial speeds of the ejected matter, while high by terrestrial standards, are not anywhere near sufficient to carry the outgoing matter to the gravitational limit before being slowed down. In the meantime, additional matter is being drawn in from the environment. Thus the general trend of both temperature and density is in the direction of reducing the size of the ionization sphere (the observable nebula). It does not follow, however, that this decrease is continuous and uniform throughout the planetary nebula stage. On the contrary, the flow conditions in the nebula are such that fluctuations of a major nature can be expected, particularly in the early portion of this evolutionary stage.
The inward flow of material toward the central star is not observable. Under ordinary conditions very diffuse material at great distances and low temperatures cannot be detected by any means now available. A part of this incoming matter is ionized by the radiation from the star, but the ionizing effect increases as the star is approached, and the transitions to lower ionization states that cause the emission of radiation are minimized. Radiation from the incoming matter is thus minor, and it has not been identified. We can, however, deduce that the initial inflow of the material, when the hot white dwarf first establishes a definite position in space, is relatively heavy, as the site of a recent supernova explosion is well filled with explosion products.
This relatively large amount of incoming matter encounters the maximum 100,000 K temperature, is strongly ionized on contact, and is ejected at a high speed. Thus a large ionization sphere is quickly established when the action begins. The outward movement of the relatively large amount of ejected matter retards the inward flow of matter to some extent. This has two effects. It reduces the amount of material reaching the central star, thereby reducing the amount of ejection, and diminishing the outward flow. Coincidentally, the incoming material that is being held back by the outward flow builds up a concentration in the regions beyond the ionization sphere. Eventually the reduced outward flow is unable to hold back this concentration of material that is being pulled inward by gravitational forces, and there is a surge of matter toward the central star. This recreates the original situation (at a somewhat lower level, since the temperature of the central star has decreased in the meantime), and the whole process is repeated.
During the time that the outward flow predominates, the density within the ionization sphere is decreasing, while because of the reduction in the inflow of cold matter, the surface temperature of the central star remains approximately constant. The ionization sphere therefore expands slowly. When the inward surge of matter occurs, these conditions undergo a rapid change. The density within the ionization sphere increases sharply, and the surface temperature of the central star decreases. The result is a rapid contraction of the ionization sphere. After these effects of the surge have run their course, the heavier outward flow and the expansion of the ionization sphere are resumed, but in the meantime the internal temperature of the central star has dropped, and the surface temperature does not regain its former level. The expansion therefore starts from a smaller size than before, and the next surge occurs before the size of the ionization sphere reaches its earlier maximum. Thus, as the successive expansions and contractions continue, the size of the nebula gradually decreases. Eventually the open space in the center is eliminated, or at least drastically reduced. The older nebulae are therefore relatively small, and have filled, or partially filled, centers.
One observed phenomenon that tends to confirm the validity of the foregoing explanation of the general behavior of the planetary nebulae is the existence of faint outer rings in some of the nebulae. These are just the kind of remnants that would be left behind if there is a relatively rapid periodic decrease in the size of the ionization sphere, as indicated in the foregoing theoretical account of the process. The currently favored explanation is that the rings were produced by explosive outbursts from the central star that preceded an outburst to which the main portion of the nebula is attributed. But there is no evidence that such explosive outbursts occur, nor does present-day astronomical theory have any explanation of how they could originate.
This is only one of many conflicts between the pattern of evolution of the planetary nebulae, as derived from the theory of the universe of motion, and the view currently prevailing among the astronomers. In that currently accepted view, these nebulae are seen as expanding objects, and the largest ones are therefore regarded as the oldest. But the temperature relations specifically contradict this hypothesis. Examination of the data reported for a selected group of “prominent” nebulae130 shows that the temperatures of the central stars range from about 100,000 K to about 30,000 K. The sizes of the nebulae vary widely, but those members of the sample group with temperatures in the neighborhood of 100,000 K all have diameters of a minute of arc or more, while almost all of those at the lower end of the temperature range have diameters of less than 30 seconds. The idea that a “dying star” that “has come close to the end of its life… destined soon to become a white dwarf, the last stage before it disappears from view altogether”129 is steadily increasing in temperature from 30,000 K to 100,000 K during the planetary stage is preposterous. Even on the basis of the astronomers own theory, the temperature trend must be downward.
It is true that the luminosity of the central star increases substantially as the size of the nebula decreases. The data reported for the sample group show that at the high end of the range of nebular sizes the average magnitude of the central star is about 14. The four with Messier numbers have magnitudes 13.5, 14, 15, and 16.5. From this level the luminosities increase rapidly, and at the low end of the nebular size range the average magnitude is about 11. These are observed, rather than absolute, magnitudes, but the correction for distance, if available, would not change the general picture. Coincidentally, the temperatures of the central stars are decreasing. It is evident that what is happening here is that while the total emission is decreasing as the stellar temperature drops, a larger proportion of that total is coming directly from the central star, rather than being passed on to the nebula and emitted from there. The decrease in temperature is the salient feature of the change that takes place with time, and it establishes the direction of evolution unequivocally.
Turning now to the question as to the location of the planetaries on the CM diagram, the first point to be noted is that we are now dealing with stars that are quite different from those on the upper side of the main sequence. As we saw in Chapter 6, these stars, Class D stars, as we are calling them, were dispersed in time by the supernova explosion, rather than being dispersed in space by the process with which we are more familiar. When they again become visible as stars they are expanding back toward the main sequence, instead of contracting. The color indexes and luminosities of these stars can be measured, and they can therefore be represented on a CM diagram. But, as we have already seen in the case of the Class C stars, the other variable properties of the stars do not necessarily maintain the same relations to the color index-luminosity function in the different star classes. For instance, the Class C mass at a given point in the diagram is usually quite different from the mass of a Class A star at that same point. The truth is that, with the exception of the spatial main sequence, which is common to all, the CM diagrams of the different classes of stars are different diagrams.
Figure 4 and the accompanying discussion in Chapter 4 bring out the fact that the major properties of Class A stars, other than those on which the CM diagram is based, are specifically related to the variables of the diagram, so that the stars of this class are alike if they have the same position on the diagram. This is not true, in general, of a Class A star and a Class C star at the same location. Similarly, if the Class D central star of a planetary nebula occupies the same position in the diagram as a certain Class A star, this does not mean that the two are alike. On the contrary, they are very different, because of their dissimilarity in the properties that are not portrayed by the diagram.
This issue does not arise in the case of most of the stars of the dwarf classes, as they are well below the spatial main sequence, but some of the large hot subdwarfs and central stars of the planetary nebulae are close to, or even above, the location of the main sequence. It should be recognized that the diagram is misleading in these cases, and that the stars of these two dwarf classes are actually very different from stars whose motion is in space. In this volume, all Class D stars will be regarded as “below the main sequence” for the purposes of the discussion.
The temperature of about 100,000 K at which the white dwarf reaches the observable region is far above the level of the environment in the material sector of the universe. In order to reach a point of thermal equilibrium in that sector the star must cool down to a level within the sector energy range (below unit speed). This cannot be accomplished in one continuous operation; a three-step process is required. Conversion to the one-dimensional material status can take place only on a single unit basis, in which a single unit of one-dimensional time motion converts to a single unit of one-dimensional space motion. The star must first cool down to a limiting temperature where the individual atoms at the stellar surface are in the unit condition in time. This is the temperature, which we have identified empirically as approximately 30,000 K. Here the transition from motion in time to motion in space takes place. The third step in the process, a further cooling to the equilibrium temperature, then follows.
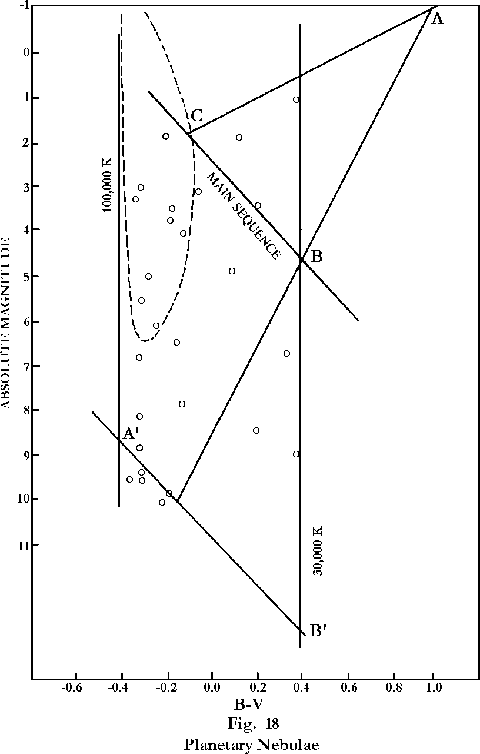
From the foregoing, we find that the planetary nebulae are located on the conventional color-magnitude version of the H-R diagram between the two vertical lines drawn in Figure 18, representing temperatures of 100,000 K and 30,000 K respectively. The plotted points are the locations of the planetary nebulae in the tabulation by G. O. Abell (reference 131). All of these points fall within the temperature limits defined by the specified lines.
For an understanding of the positions and evolutionary changes illustrated by Figure 18 we need to review some of the findings of the previous volumes of this series with respect to natural units. According to the fundamental postulates of the theory of the universe of motion, the basic constituent of the universe, motion, is limited to discrete units. Since all physical phenomena in this universe are motions, combinations of motions, or relations between motions, it follows from the discrete nature of the units of motion that all of these subsidiary phenomena must also be limited to discrete units.
The basic units of space, time, mass, energy, etc., were evaluated in Volume I. However, these simple units are not directly applicable to complex phenomena. Here a compound unit usually applies, a combination of the simple primary units. For example, the primary unit of space has been evaluated as 4.56×10-6 cm. But within a unit of space there are compound motions in which the spatial units are modified by certain combinations of units of time. As a result, the phenomena in this region are not related to the simple units of space, but to a compound (or modified) unit of space that amounts to 0.0064 of the full-sized natural unit, or 2.92×10-8 cm.
Because of the general applicability of the discrete unit limitation, we can deduce that wherever we encounter a critical value of some kind, we are dealing with a compound unit, or a small number of such units. It is not usually possible to evaluate the compound unit in terms of the simple units of which it is composed until after the theoretical relations that are applicable have been clarified in considerable detail. For instance, in the case of the space units, the factor 0.0064 that relates the compound unit to the simple unit is something that one would not be likely to find unless he had a very good idea as to where to look for it. The development of the theory of the universe of motion has not yet been applied to the quantitative aspects of astronomical phenomena on an extensive enough scale to enable evaluating more than a limited number of the compound astronomical units. But the mere knowledge that some particular magnitude is a compound unit, or a small whole number of such units, is very often helpful.
In the present instance, we are able to make use of a feature of the
evolutionary pattern of the globular clusters that was mentioned, but not discussed, in Chapter 8. As noted there, the difference in luminosity between point A and point B on the CM diagram, on the logarithmic scale, is twice the difference between point B and point C. Inasmuch as these points are all critical points in the evolutionary pattern, the difference in magnitude between any two of them is presumably n compound units, where n is a small whole number.
The nature of this compound unit has not yet been determined, but the logarithmic magnitude scale suggests a dimensional relation, and leads to the surmise that the magnitudes at points B. C, and A are 1, 2, and 3 respectively. There is, of course, a large hypothetical component in this conclusion, at the present stage of theoretical and observational knowledge, but we can treat it like any other hypothesis; that is, develop its consequences and compare them with observation. As will be seen in the discussion that follows, the consequences of this hypothesis do, in fact, agree with the available observational information. Within the limits to which the correlation has been carried, the hypothesis has been verified.
The particular value of this hypothesis is that it gives us a means of locating the critical points in the white dwarf section of the CM diagram. In the earlier volumes it was established that the boundary between motion in space and motion in time has a finite width, and that there are two natural units between the respective unit levels. It follows that if, as we have concluded, point B corresponds to one unit in the spatial direction (+1 we may say), then a point one unit lower on the extension of the line AB corresponds to zero, and point B’, two units lower, corresponds to -1; that is, one unit in the temporal direction. The line APB’ parallel to BC is then the equivalent of the main sequence for motion in time.
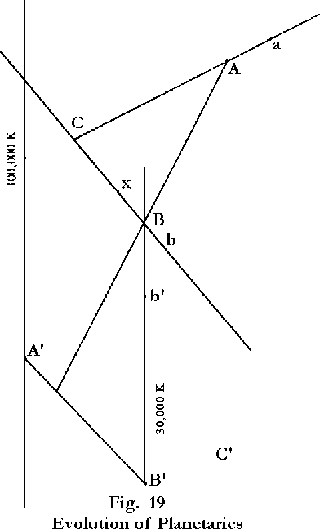
With the benefit of this information we can now define the evolutionary paths of the planetary stars. Figure 19 compares these paths with those of the giant stars. The line OAB is the evolutionary pattern of a giant star that has a mass of about 1.1 solar units at point B. Such a star originates with a smaller mass, but secretes material as it moves along line OA, and reaches the 1.1 mass level at point A. This is the critical density level, where the star acquires the ability to contract by means of its own gravitation, without the aid of outside forces. This contraction carries it down to the point of gravitational equilibrium at B.
This star that begins its life as a red giant is in a state of thermal equilibrium; that is, it is radiating the same amount of heat that it generates. But its density is extremely low, far below the level of stability. Its evolutionary course beyond point A, unless modified by accretion, is therefore along a line of constant central temperature toward the main sequence, the location of gravitational equilibrium. The early white dwarf, on the other hand, is already in a state of gravitational equilibrium, from the standpoint of gravitation in space, while it is too hot to be thermally stable. This star therefore moves
along the line of gravitational equilibrium for motion in time, the equivalent of the spatial main sequence, toward a condition of thermal equilibrium.
The (inverse) volume of the white dwarf star at any given surface temperature is determined by the mass. Thus the more massive stars reach the 100,000 K temperature level while their inverse volume. from which they radiate (a point that will be considered further in Chapter 12) is greater, and their luminosity is consequently higher. The incoming white dwarfs are thus distributed along the 100,000 K line in accordance with their masses. At the 1.1 level, identified as A’ in Figure 19, the white dwarf occupies a critical position somewhat similar to the critical density position at point A on the giant path. T his white dwarf of 1.1 solar masses is the smallest star that has sufficient total thermal energy to maintain the 100,000 K surface temperature in the gaseous type of gravitational equilibrium.
This critical mass star that originates at point A’ moves down along the line A’B’, gradually converting its outermost atoms from three-dimensional motion in time to one-dimensional motion in time. This conversion is completed at B’. Further cooling then transforms the one-dimensional motion in time at B’ to one-dimensional motion in space at B. Thus the giant and dwarf stars of the same mass eventually arrive at the same point on the spatial main sequence.
Giant stars whose growth ceases at some point a between O and A follow a path ab parallel to AB, terminating at point b on the main sequence. Stars that continue adding matter beyond point A have a different evolutionary pattern, as previously explained. In the dwarf region it is the star with a mass less than 1.1 solar units that has a different pattern of evolution, one that will be examined in Chapter 12. Since the mass of the white dwarf is constant during its movement along the line of gravitational equilibrium, it follows that each mass has its own equilibrium line. Thus the equivalent of the main sequence for motion in time is a series of lines parallel to the spatial main sequence.
The larger stars that we are now considering originate along the 100,000 K temperature line at locations above point A’. Such a star moves along a path a’b’ from a’, the point of origin, to b’, a point on the line B’B. It then converts to motion in space at point B in the same manner as the star of mass 1.1, but B is not a location of thermal equilibrium for the more massive star. A further movement along the main sequence is required in order to reach the point of thermal stability. The final position of this star in the CM diagram is a point somewhere between B and C, the exact location depending on the mass.
On the diagram, the movement from B to x, the final location, appears anomalous, as a decrease in temperature normally corresponds to a movement to the right. This is another illustration of the fact that the CM diagrams of stars of different classes, or even different sub-classes, are actually different diagrams. The temperature corresponding to a given color index is much lower on the spatial main sequence than on the equivalent path a’b’ for motion in time. The movement of the Class D stars toward the left after reaching the spatial main sequence is not a temperature effect, but a result of this difference in the significance of positions in the diagram. The cooling star is actually at a considerably lower temperature in its final position at point x than it was at point b’, even though it is farther to the left.
Inasmuch as the white dwarfs are contracting in time rather than in space, the spatial compression due to the gravitational motion toward the galactic center has no effect on these Class D stars. The evolutionary paths shown in Figure 19 therefore meet at the globular cluster level of the spatial main sequence, rather than at the position of the galactic field stars. The final position, designated x, on the spatial main sequence is, however, subject to the gravitational shift, and the last phase of the conversion from motion in time to motion in space includes an upward movement of 0.8 magnitudes, as well as the movement to the left from B to x. As noted in Chapter 10, the observed Class D pattern is strong evidence of the reality of the gravitational shift.
Observational information about the two classes of relatively large white dwarfs that we have been considering, the hot subdwarfs and their successors, the central stars of the planetary nebulae, is very limited, but the positions on the CM diagram indicated by the available data are entirely consistent with the evolutionary pattern that we have derived from theory. The dashed line in Figure 18 outlines the locations of the hot subdwarfs as given by M. and G. Burbidge (reference 102). This indicated area is clearly consistent with the theoretical conclusions. As noted earlier, the locations of the representative group of planetary nebulae identified in Figure 18 are also within the theoretical limits.
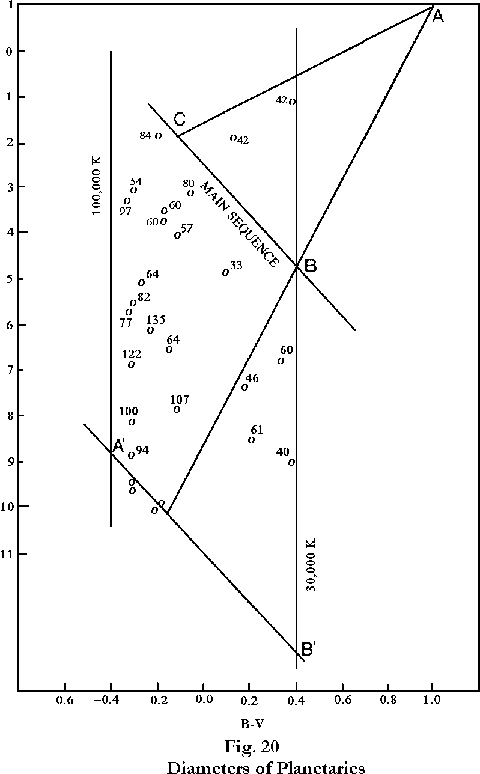
Because of their decrease in temperature, the movement of these nebulae on the CM diagram must be, at least generally, from left to right. (Even the adherents of conventional astronomical theory concede this. See, for instance, the diagram by Pasachoff, reference 132.) Some further confirmation of the theoretical findings can therefore be obtained by examination of the relation of the diameters of the planetaries on the Abell list to their locations on the diagram. Figure 20 is a reproduction of Figure 18, with the diameters in parsecs shown alongside the points indicating the locations. As might be expected, in view of the diversity of the conditions under which the nebulae exist, and to which the observations are subject, there are wide unexplained variations in the individual values, but the general trend is clear. Disregarding the group of nebulae below the line A’B’, which are subject to some special considerations that we will examine in Chapter 12, there are 16 nebulae with an average diameter of 84 parsecs in the left half of the identified nebular region, and 7 nebulae with an average diameter of 47 parsecs in the right half.
Observational information on the masses of the planetary stars is minimal, but the little that is available is consistent with the existence of a lower limit at 1.1 solar masses, or at least not inconsistent with it. An average of 1.2 solar masses has been suggested.“133 As noted earlier, the mass of one of the pre-planetary stars, the hot sub-dwarfs, has been determined as 1.5 on the same scale. We will see in Chapter 13 that the mass of another star, which we will identify as a former planetary star, has been calculated at 2.1 solar masses. These results are too few in number to confirm the theoretical minimum, but they do point in that direction.
Inasmuch as this shortage of empirical information exists, in one degree or another, throughout the entire range of the white dwarf phenomena, it is again appropriate to call attention to the fact that the validity of the general principles and relations that have been, and will be, applied to explaining these phenomena has already been firmly established in physical fields where factual
data are abundant and reliable. Thus, even though the correlations between theory and observation that are possible in such areas as that of the white dwarfs are too limited to provide positive confirmation of the validity of the theoretical conclusions, the fact that these conclusions are consistent with what is known from observation is sufficient, in conjunction with the validity of the principles on which they are based, to establish a strong probability that they are correct.
It was noted in Chapter 6 that some of the central stars of planetary nebulae are currently identified as Wolf-Rayet stars. The identification is based on their high temperatures and spectra that are similar to those of the massive Wolf-Rayets. In other respects these objects are quite different. As described by Smith and Aller, the central stars of the planetary nebulae are believed to have masses in the neighborhood of solar, and absolute magnitudes fainter than -3, whereas the Wolf-Rayet stars in the other class are believed to average about ten solar masses and to have absolute magnitudes brighter than -4. A comparison of typical stars of these two classes leads these authors to the conclusion that they have a “totally different evolutionary status.” They admit that they “are led to wonder how many different stages of evolution can yield the Wolf-Rayet form of spectrum.”134
“It is a further problem,” says Anne B. Underhill, “to understand… why this physical state may occur early in the life of a massive star (the Wolf-Rayet stars of Population 1) and late in the life of a star of small mass (the Wolf-Rayet stars of the disk population.”75 This problem is resolved by our finding that the planetary stage follows almost immediately after the Wolf-Rayet stage; that is, the true Wolf-Rayet is a late pre-explosion star, whereas the central star of a planetary nebula currently confused with the Wolf-Rayet is an early post-explosion star. The similarity of the spectra is no doubt due to the existence of very high temperatures in both cases, and to the presence, in both classes of stars, of matter from the stellar interiors that has been brought to the surface by explosive activity.
According to the general description of the dwarf star cycle given in Chapter 4, and the identification of the evolutionary pattern in Figure 19, the white dwarfs ultimately make their way back to positions on the spatial main sequence. We have now traced the course of one group of these stars along lines parallel to the main sequence from their points of entry into the observable region to positions somewhere near the low temperature limit in the neighborhood of 30,000 K. As has been indicated, the next move will be upward toward the main sequence. Before discussing the nature of the change that takes place in this final dwarf stage, however it will be advisable to examine another group of white dwarf stars that also has to undergo this final transition to the material status.